2.2 Modelos lineales generalizados
Los modelos lineales generalizados son una extensión de los modelos lineales para el caso de que la distribución condicional de la variable respuesta no sea normal (por ejemplo, discreta: Bernoulli, Binomial, Poisson…). En los modelos lineales generalizados se introduce una función invertible g, denominada función enlace (o link) de forma que: \[g\left(E(Y | \mathbf{X} )\right) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p}\] y su ajuste, en la práctica, se realiza empleando el método de máxima verosimilitud (habrá que especificar también una familia de distribuciones para la respuesta).
La función de enlace debe ser invertible, de forma que se pueda volver a transformar el modelo ajustado (en la escala lineal de las puntuaciones) a la escala original. Por ejemplo, como se comentó al final de la Sección 1.2.1, para modelar una variable indicadora, con distribución de Bernoulli (caso particular de la Binomial) donde \(E(Y | \mathbf{X} ) = p(\mathbf{X})\) es la probabilidad de éxito, podemos considerar la función logit \[\operatorname{logit}(p(\mathbf{X}))=\log\left( \frac{p(\mathbf{X})}{1-p(\mathbf{X})} \right) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p}\] (que proyecta el intervalo \([0, 1]\) en \(\mathbb{R}\)), siendo su inversa la función logística \[p(\mathbf{X}) = \frac{e^{\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p}}}{1 + e^{\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p}}}\] Esto da lugar al modelo de regresión logística (múltiple), que será el que utilizaremos como ejemplo en esta sección. Para un tratamiento más completo de los métodos de regresión lineal generalizada, se recomienda consultar alguno de los libros de referencia, como Hastie y Pregibon (1991), Faraway (2016), Dunn y Smyth (2018) o McCullagh (2019).
Para el ajuste (estimación de los parámetros) de un modelo lineal generalizado a un conjunto de datos (por máxima verosimilitud) se emplea la función glm():
ajuste <- glm(formula, family = gaussian, data, weights, subset, ...)La mayoría de los principales parámetros coinciden con los de la función lm().
El parámetro family especifica la distribución y, opcionalmente, la función de enlace.
Por ejemplo:
gaussian(link = "identity"),gaussian(link = "log")binomial(link = "logit"),binomial(link = "probit")poisson(link = "log")Gamma(link = "inverse")
Para cada distribución se toma por defecto una función de enlace (el denominado enlace canónico, mostrado en primer lugar en la lista anterior; ver help(family) para más detalles).
Así, en el caso del modelo logístico bastará con establecer family = binomial.
También se puede emplear la función bigglm() del paquete biglm para ajustar modelos lineales generalizados a grandes conjuntos de datos, aunque en este caso los requerimientos computacionales pueden ser mayores.
Como se comentó en la Sección 2.1, muchas de las herramientas y funciones genéricas disponibles para los modelos lineales son válidas también para este tipo de modelos, como por ejemplo las mostradas en las tablas 2.1 y 2.2.
Como ejemplo, continuaremos con los datos de grasa corporal, pero utilizando como respuesta una nueva variable bfan indicadora de un porcentaje de grasa corporal superior al rango considerado normal.
Además, añadimos el índice de masa corporal como predictor, empleado habitualmente para establecer el grado de obesidad de un individuo (este conjunto de datos está disponible en mpae::bfan).
df <- bodyfat
# Grasa corporal superior al rango normal
df[1] <- factor(df$bodyfat > 24 , # levels = c('FALSE', 'TRUE'),
labels = c('No', 'Yes'))
names(df)[1] <- "bfan"
# Indice de masa corporal (kg/m2)
df$bmi <- with(df, weight/(height/100)^2)
set.seed(1)
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]Es habitual empezar realizando un análisis descriptivo. Si el número de variables no es muy grande, podemos generar un gráfico de dispersión matricial, diferenciando las observaciones pertenecientes a las distintas clases (ver Figura 2.11).
plot(train[-1], pch = as.numeric(train$bfan), col = as.numeric(train$bfan))
Figura 2.11: Gráfico de dispersión matricial, con colores y símbolos dependiendo de bfan.
Para ajustar un modelo de regresión logística bastaría con establecer el argumento family = binomial en la llamada a glm() (por defecto utiliza link = "logit").
Por ejemplo, podríamos considerar como punto de partida los predictores seleccionados para regresión en el apartado anterior:
modelo <- glm(bfan ~ abdomen + wrist + height, family = binomial,
data = train)
modelo##
## Call: glm(formula = bfan ~ abdomen + wrist + height, family = binomial,
## data = train)
##
## Coefficients:
## (Intercept) abdomen wrist height
## 1.859 0.341 -0.906 -0.104
##
## Degrees of Freedom: 195 Total (i.e. Null); 192 Residual
## Null Deviance: 229
## Residual Deviance: 116 AIC: 124La razón de ventajas (odds ratio; OR) permite cuantificar el efecto de las variables explicativas en la respuesta (incremento proporcional en la razón entre la probabilidad de éxito y la de fracaso, al aumentar una unidad la variable manteniendo las demás fijas):
exp(coef(modelo)) # Razones de ventajas ("odds ratios")## (Intercept) abdomen wrist height
## 6.41847 1.40621 0.40402 0.90082Para obtener un resumen más completo del ajuste se puede utilizar summary():
summary(modelo)##
## Call:
## glm(formula = bfan ~ abdomen + wrist + height, family = binomial,
## data = train)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.8592 7.3354 0.25 0.800
## abdomen 0.3409 0.0562 6.07 1.3e-09 ***
## wrist -0.9063 0.3697 -2.45 0.014 *
## height -0.1044 0.0445 -2.35 0.019 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 228.80 on 195 degrees of freedom
## Residual deviance: 116.14 on 192 degrees of freedom
## AIC: 124.1
##
## Number of Fisher Scoring iterations: 6La desvianza (deviance) es una medida de la bondad del ajuste de un modelo lineal generalizado (sería equivalente a la suma de cuadrados residual de un modelo lineal; valores más altos indican peor ajuste). La null deviance se correspondería con un modelo solo con la constante, y la residual deviance, con el modelo ajustado. En este caso hay una reducción de 112.65 con una pérdida de 3 grados de libertad (una reducción significativa).
Para contrastar globalmente el efecto de las covariables también podemos emplear:
modelo.null <- glm(bfan ~ 1, binomial, data = train)
anova(modelo.null, modelo, test = "Chi")## Analysis of Deviance Table
##
## Model 1: bfan ~ 1
## Model 2: bfan ~ abdomen + wrist + height
## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
## 1 195 229
## 2 192 116 3 113 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 12.2.1 Selección de variables explicativas
El objetivo es conseguir un buen ajuste con el menor número de variables explicativas posible.
Al igual que en el caso del modelo de regresión lineal múltiple, se puede seguir un proceso interactivo, eliminando o añadiendo variables con la función update(), aunque también están disponibles métodos automáticos de selección de variables.
Para obtener el modelo “óptimo” lo ideal sería evaluar todos los modelos posibles.
En este caso no se puede emplear la función regsubsets() del paquete leaps (solo disponible para modelos lineales),
pero el paquete
bestglm
proporciona una herramienta equivalente, bestglm().
También se puede emplear la función stepwise() del paquete RcmdrMisc para seleccionar un modelo por pasos según criterio AIC o BIC:
# library(RcmdrMisc)
modelo.completo <- glm(bfan ~ ., family = binomial, data = train)
modelo <- stepwise(modelo.completo, direction = "forward/backward",
criterion = "BIC")##
## Direction: forward/backward
## Criterion: BIC
##
## Start: AIC=234.07
## bfan ~ 1
##
## Df Deviance AIC
## + abdomen 1 132 142
## + bmi 1 156 167
## + chest 1 163 174
## + hip 1 176 186
## + weight 1 180 190
## + knee 1 195 206
## + thigh 1 197 207
## + neck 1 197 208
## + biceps 1 201 212
## + forearm 1 216 226
## + wrist 1 218 229
## + age 1 219 230
## + ankle 1 223 234
## <none> 229 234
## + height 1 229 239
##
## Step: AIC=142.07
## bfan ~ abdomen
##
## Df Deviance AIC
## + weight 1 117 133
## + wrist 1 122 138
## + height 1 123 138
## + ankle 1 125 141
## <none> 132 142
## + age 1 127 143
## + hip 1 127 143
## + thigh 1 127 143
## + forearm 1 128 143
## + neck 1 128 144
## + chest 1 128 144
## + biceps 1 129 145
## + knee 1 129 145
## + bmi 1 131 147
## - abdomen 1 229 234
##
## Step: AIC=133.06
## bfan ~ abdomen + weight
##
## Df Deviance AIC
## <none> 117 133
## + wrist 1 114 135
## + knee 1 116 137
## + hip 1 116 137
## + bmi 1 116 137
## + height 1 117 138
## + biceps 1 117 138
## + neck 1 117 138
## + ankle 1 117 138
## + age 1 117 138
## + chest 1 117 138
## + thigh 1 117 138
## + forearm 1 117 138
## - weight 1 132 142
## - abdomen 1 180 190summary(modelo)##
## Call:
## glm(formula = bfan ~ abdomen + weight, family = binomial, data = train)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -30.2831 4.6664 -6.49 8.6e-11 ***
## abdomen 0.4517 0.0817 5.53 3.2e-08 ***
## weight -0.1644 0.0487 -3.38 0.00073 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 228.80 on 195 degrees of freedom
## Residual deviance: 117.22 on 193 degrees of freedom
## AIC: 123.2
##
## Number of Fisher Scoring iterations: 62.2.2 Análisis e interpretación del modelo
Las hipótesis estructurales del modelo son similares al caso de regresión lineal (aunque algunas como la linealidad se suponen en la escala transformada). Si no se verifican, los resultados basados en la teoría estadística pueden no ser fiables o ser totalmente erróneos.
Con el método plot() se pueden generar gráficos de interés para la diagnosis del modelo (ver Figura 2.12):
plot(modelo)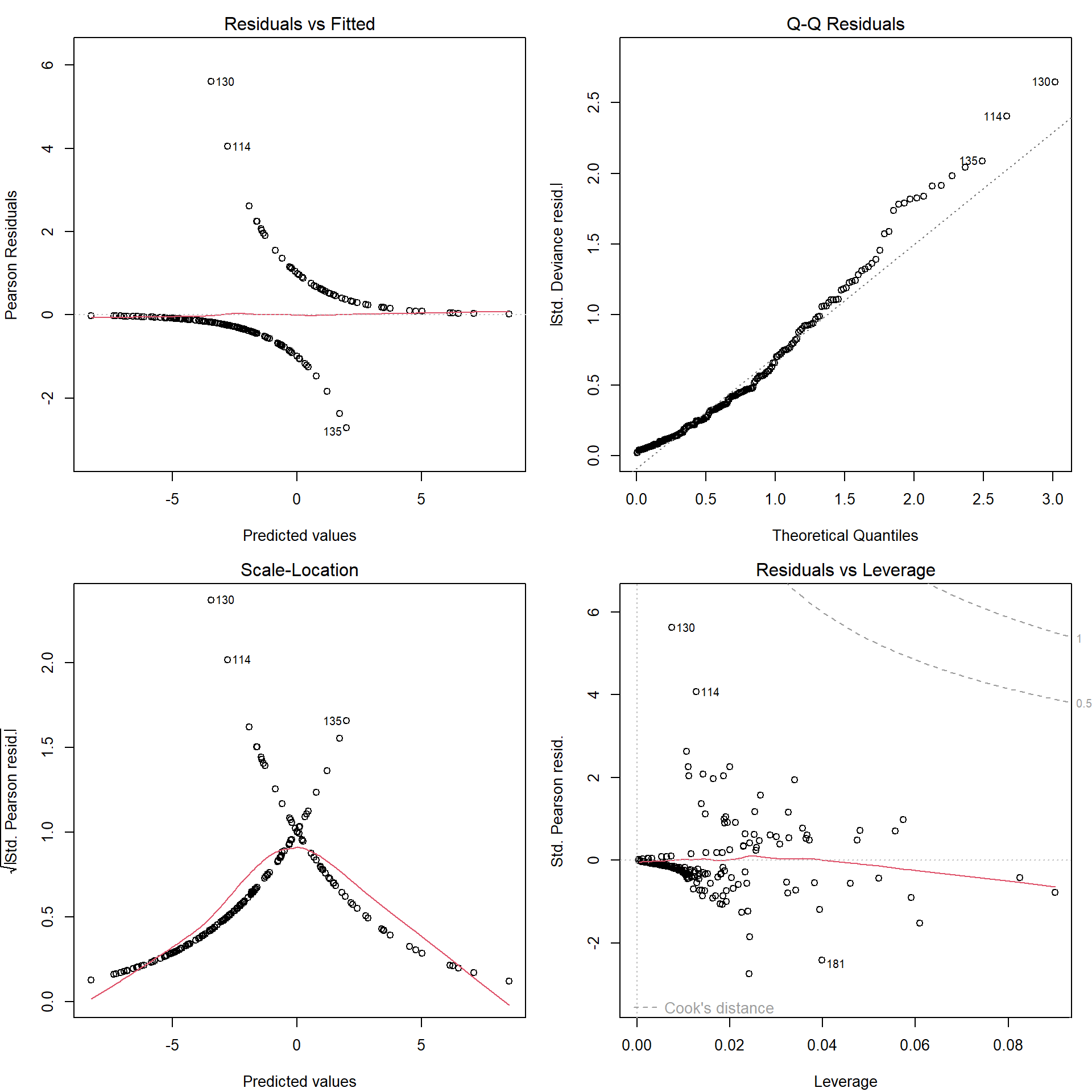
Figura 2.12: Gráficos de diagnóstico del ajuste lineal generalizado.
Su interpretación es similar a la de los modelos lineales (consultar las referencias incluidas al principio de la sección para más detalles).
En este caso destacan dos posibles datos atípicos, aunque aparentemente no son muy influyentes a posteriori (en el modelo ajustado).
Adicionalmente, se pueden generar gráficos parciales de residuos, por ejemplo con la función crPlots() del paquete car (ver Figura 2.13):
outliers <- which(abs(residuals(modelo, type = "pearson")) > 3)
crPlots(modelo, id = list(method = outliers, col = 2), main = "")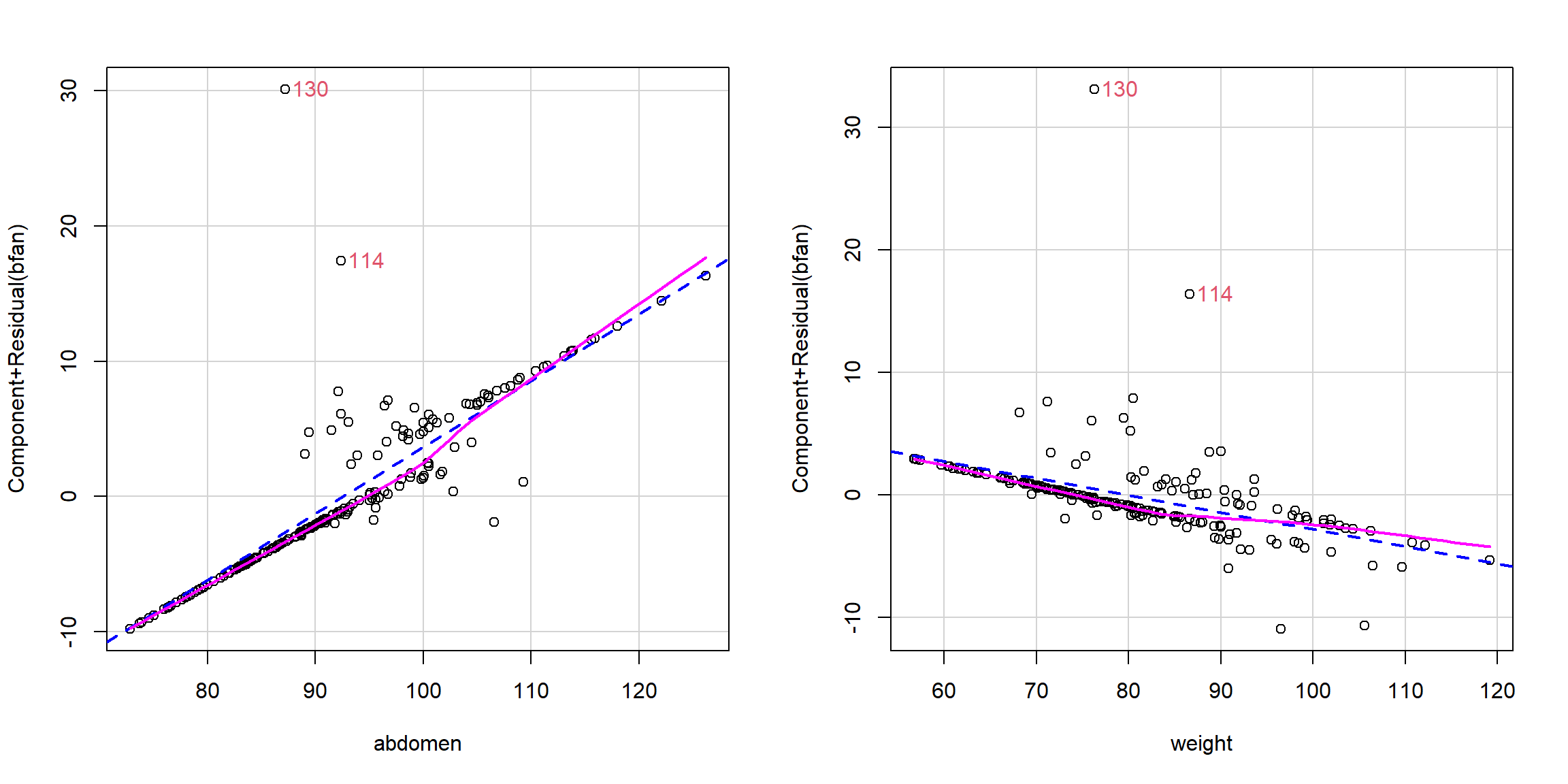
Figura 2.13: Gráficos parciales de residuos del ajuste generalizado.
Se pueden emplear las mismas funciones vistas en los modelos lineales para obtener medidas de diagnosis de interés (tablas 2.1 y 2.2). Por ejemplo, residuals(model, type = "deviance") proporcionará los residuos deviance.
Por supuesto, también pueden aparecer problemas de colinealidad, y podemos emplear las mismas herramientas para detectarla:
vif(modelo)## abdomen weight
## 4.5443 4.5443Si no se satisfacen los supuestos básicos, también se pueden intentar distintas alternativas (se puede cambiar la función de enlace y la familia de distribuciones, que puede incluir parámetros para modelar dispersión, además de las descritas en la Sección 2.1.3), incluyendo emplear modelos más flexibles o técnicas de aprendizaje estadístico que no dependan de ellas (sustancialmente). En el Capítulo 6 (y siguientes) se tratarán extensiones de este modelo.
Ejercicio 2.3 Vuelve a ajustar el modelo anterior eliminando las observaciones atípicas determinadas por outliers <- which(abs(residuals(modelo, type = "pearson")) > 3) y estudia si hay grandes cambios en las estimaciones de los coeficientes.
Repite también el proceso de selección de variables para confirmar que estas observaciones no influyen en el resultado32.
2.2.3 Evaluación de la precisión
Para evaluar la calidad de la predicción en nuevas observaciones podemos seguir los pasos mostrados en la Sección 1.3.5.
Las estimaciones de la probabilidad (de la segunda categoría) se obtienen empleando predict() con type = "response":
p.est <- predict(modelo, type = "response", newdata = test)
pred.glm <- factor(p.est > 0.5, labels = c("No", "Yes"))y las medidas de precisión de la predicción (además de los criterios AIC o BIC tradicionales):
caret::confusionMatrix(pred.glm, test$bfan, positive = "Yes",
mode = "everything")## Confusion Matrix and Statistics
##
## Reference
## Prediction No Yes
## No 27 5
## Yes 2 16
##
## Accuracy : 0.86
## 95% CI : (0.733, 0.942)
## No Information Rate : 0.58
## P-Value [Acc > NIR] : 1.96e-05
##
## Kappa : 0.707
##
## Mcnemar's Test P-Value : 0.45
##
## Sensitivity : 0.762
## Specificity : 0.931
## Pos Pred Value : 0.889
## Neg Pred Value : 0.844
## Precision : 0.889
## Recall : 0.762
## F1 : 0.821
## Prevalence : 0.420
## Detection Rate : 0.320
## Detection Prevalence : 0.360
## Balanced Accuracy : 0.846
##
## 'Positive' Class : Yes
## o de las estimaciones de las probabilidades (como el AUC).
Ejercicio 2.4 En este ejercicio se empleará el conjunto de datos winetaste del paquete mpae (Cortez et al., 2009) que contiene información fisico-química y sensorial de una muestra de 1250 vinos portugueses de la variedad vinho verde (para más detalles, consultar las secciones 3.3.1 y 3.3.2).
Considerando como respuesta la variable taste, que clasifica los vinos en “good” o “bad” a partir de evaluaciones realizadas por expertos:
Particiona los datos, considerando un 80 % de las observaciones como muestra de entrenamiento y el resto como muestra de test.
Ajusta dos modelos de regresión logística empleando los datos de entrenamiento, uno seleccionando las variables por pasos hacia delante (
forward) y otro hacia atrás (backward).Estudia si hay problemas de colinealidad en los modelos.
Evalúa la capacidad predictiva de ambos modelos en la muestra
test.
Bibliografía
Normalmente se sigue un proceso iterativo, eliminando la más atípica (o influyente) en cada paso, hasta que ninguna observación se identifique como atípica (o influyente). En este caso podríamos emplear
which.max(abs(residuals(modelo, type = "pearson"))).↩︎