5.2 Clasificadores de soporte vectorial
Los clasificadores de soporte vectorial (support vector classifiers; también denominados soft margin classifiers) fueron introducidos en Cortes y Vapnik (1995). Son una extensión del problema anterior que se utiliza cuando se desea clasificar mediante un hiperplano, pero no existe ninguno que separe perfectamente los datos de entrenamiento según su categoría. En este caso no queda más remedio que admitir errores en la clasificación de algunos datos de entrenamiento (como hemos visto que pasa con todas las metodologías), que van a estar en el lado equivocado del hiperplano. Y en lugar de hablar de un margen, se habla de un margen débil (soft margin).
Este enfoque, consistente en aceptar que algunos datos de entrenamiento van a estar mal clasificados, puede ser preferible aunque exista un hiperplano que resuelva el problema de la sección anterior, ya que los clasificadores de soporte vectorial son más robustos que los clasificadores de máximo margen.
Veamos la formulación matemática del problema: \[\mbox{max}_{\beta_0, \beta_1,\ldots, \beta_p, \epsilon_1,\ldots, \epsilon_n} M\] sujeto a \[\sum_{j=1}^p \beta_j^2 = 1\] \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) \ge M(1 - \epsilon_i) \ \ \forall i\] \[\sum_{i=1}^n \epsilon_i \le K\] \[\epsilon_i \ge 0 \ \ \forall i\]
Las variables \(\epsilon_i\) son las variables de holgura (slack variables). Quizás resultase más intuitivo introducir las holguras en términos absolutos, como \(M -\epsilon_i\), pero eso daría lugar a un problema no convexo, mientras que escribiendo la restricción en términos relativos como \(M(1 - \epsilon_i)\) el problema pasa a ser convexo.
En esta formulación el elemento clave es la introducción del hiperparámetro \(K\), necesariamente no negativo, que se puede interpretar como la tolerancia al error. De hecho, es fácil ver que no puede haber más de \(K\) datos de entrenamiento incorrectamente clasificados, ya que si un dato está mal clasificado, entonces \(\epsilon_i > 1\). En el caso extremo de utilizar \(K = 0\), estaríamos en el caso de un hard margin classifier. La elección del valor de \(K\) también se puede interpretar como una penalización por la complejidad del modelo, y por tanto en términos del balance entre el sesgo y la varianza: valores pequeños van a dar lugar a modelos muy complejos, con mucha varianza y poco sesgo (con el consiguiente riesgo de sobreajuste); y valores grandes, a modelos con mucho sesgo y poca varianza. El hiperparámetro \(K\) se puede seleccionar de modo óptimo por los procedimientos ya conocidos, tipo bootstrap o validación cruzada.
Una forma equivalente de formular el problema (cuadrático con restricciones lineales) es \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \lVert \boldsymbol{\beta} \rVert\] sujeto a \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) \ge 1 - \epsilon_i \ \ \forall i\] \[\sum_{i=1}^n \epsilon_i \le K\] \[\epsilon_i \ge 0 \ \ \forall i\]
En la práctica, por una conveniencia de cálculo, se utiliza la formulación equivalente \[\mbox{min}_{\beta_0, \boldsymbol{\beta}} \frac{1}{2}\lVert \boldsymbol{\beta} \rVert^2 + C \sum_{i=1}^n \epsilon_i\] sujeto a \[ y_i(\beta_0 + \beta_1 x_{1i} + \beta_2 x_{2i} + \ldots + \beta_p x_{pi}) \ge 1 - \epsilon_i \ \ \forall i\] \[\epsilon_i \ge 0 \ \ \forall i\]
Aunque el problema a resolver es el mismo, y por tanto también la solución, hay que tener cuidado con la interpretación, pues el hiperparámetro \(K\) se ha sustituido por \(C\). Este nuevo parámetro es el que nos vamos a encontrar en los ejercicios prácticos y tiene una interpretación inversa a \(K\). El parámetro \(C\) es la penalización por mala clasificación (coste que supone que un dato de entrenamiento esté mal clasificado), y por tanto el hard margin classifier se obtiene para valores muy grandes (\(C = \infty\) se corresponde con \(K = 0\)), como se ilustra en la Figura 5.2. Esto es algo confuso, ya que no se corresponde con la interpretación habitual de penalización por complejidad.
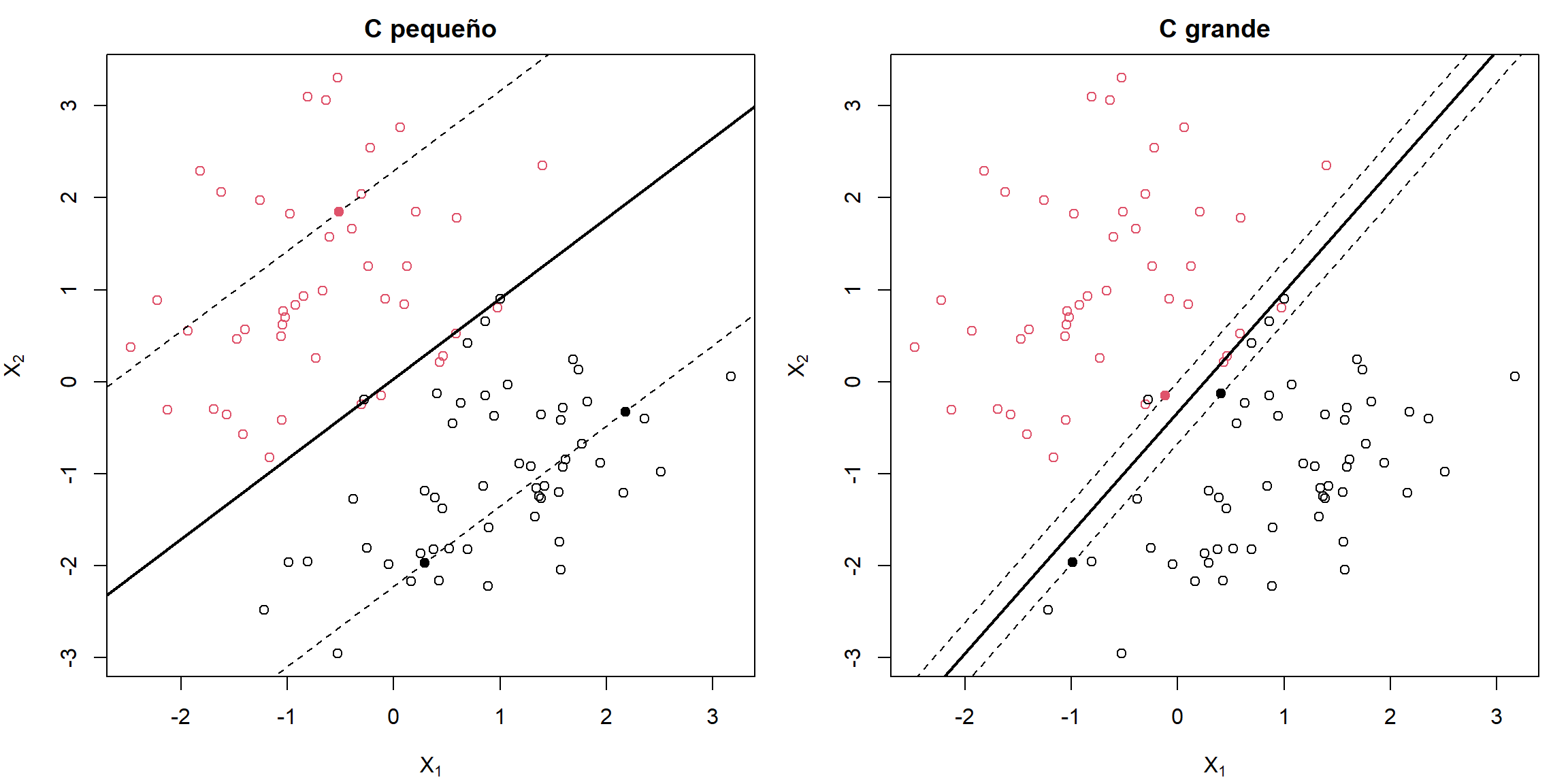
Figura 5.2: Ejemplo de clasificadores de soporte vectorial (margen débil), con parámetro de coste “pequeño” (izquierda) y “grande” (derecha).
En este contexto, los vectores soporte van a ser no solo los datos de entrenamiento que están (correctamente clasificados) a una distancia \(M\) del hiperplano, sino también aquellos que están incorrectamente clasificados e incluso los que están a una distancia inferior a \(M\). Como se comentó en la sección anterior, estos son los datos que definen el modelo, que es por tanto robusto a las observaciones que están lejos del hiperplano.
Aunque no vamos a entrar en detalles sobre cómo se obtiene la solución del problema de optimización, sí resulta interesante destacar que el clasificador de soporte vectorial \[m(\mathbf{x}) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p\] puede representarse como \[m(\mathbf{x}) = \beta_0 + \sum_{i=1}^n \alpha_i \mathbf{x}^t \mathbf{x}_i\] donde \(\mathbf{x}^t \mathbf{x}_i\) es el producto escalar entre el vector \(\mathbf{x}\) del dato a clasificar y el vector \(\mathbf{x}_i\) del dato de entrenamiento \(i\)-ésimo. Asimismo, los coeficientes \(\beta_0, \alpha_1, \ldots, \alpha_n\) se obtienen (exclusivamente) a partir de los productos escalares \(\mathbf{x}_i^t \mathbf{x}_j\) de los distintos pares de datos de entrenamiento y de las respuestas \(y_i\). Y más aún, el sumatorio anterior se puede reducir a los índices que corresponden a vectores soporte (\(i\in S\)), al ser los demás coeficientes nulos: \[m(\mathbf{x}) = \beta_0 + \sum_{i\in S} \alpha_i \mathbf{x}^t \mathbf{x}_i\]