7.3 Modelos aditivos

En los modelos aditivos se supone que: \[Y= \beta_{0} + f_1(X_1) + f_2(X_2) + \ldots + f_p(X_p) + \varepsilon\] siendo $f_{i},$ $i=1,...,p,$ funciones cualesquiera. De esta forma se consigue mucha mayor flexibilidad que con los modelos lineales, pero manteniendo la interpretabilidad de los efectos de los predictores. Adicionalmente, se puede considerar una función de enlace, obteniéndose los denominados modelos aditivos generalizados (GAM). Para más detalles sobre estos modelos, ver Hastie y Tibshirani (1990) o Wood (2017).

Los modelos lineales (análogamente los modelos lineales generalizados) son un caso particular, considerando $f_{i}(x) = \beta_{i}x$. Se pueden utilizar cualesquiera de los métodos de suavizado descritos anteriormente para construir las componentes no paramétricas. Así, por ejemplo, si se emplean splines naturales de regresión, el ajuste se reduce al de un modelo lineal. Se podrían considerar distintas aproximaciones para el modelado de cada componente (modelos semiparamétricos) y realizar el ajuste mediante backfitting (se ajusta cada componente de forma iterativa, empleando los residuos obtenidos al mantener las demás fijas). Si en las componentes no paramétricas se emplean únicamente splines de regresión (con o sin penalización), se puede reformular el modelo como un GLM (regularizado si hay penalización) y ajustarlo fácilmente adaptando herramientas disponibles (penalized re-weighted iterative least squares, PIRLS).

De entre los numerosos paquetes de R que implementan estos modelos destacan:

gam: Admite splines de suavizado (univariantes, s()) y regresión polinómica local (multivariante, lo()), pero no dispone de un método para la selección automática de los parámetros de suavizado (se podría emplear un criterio por pasos para la selección de componentes). Sigue la referencia Hastie y Tibshirani (1990).
mgcv: Admite una gran variedad de splines de regresión y splines penalizados (s(); por defecto emplea thin plate regression splines penalizados multivariantes), con la opción de selección automática de los parámetros de suavizado mediante distintos criterios. Además de que se podría emplear un método por pasos, permite la selección de componentes mediante regularización. Al ser más completo que el anterior, sería el recomendado en la mayoría de los casos (ver ?mgcv::mgcv.package para una introducción al paquete). Sigue la referencia Wood (2017).

La función gam() del paquete mgcv permite ajustar modelos aditivos generalizados empleando suavizado mediante splines:

ajuste <- gam(formula, family = gaussian, data, ...)

También dispone de la función bam() para el ajuste de estos modelos a grandes conjuntos de datos, y de la función gamm() para el ajuste de modelos aditivos generalizados mixtos, incluyendo dependencia en los errores. El modelo se establece a partir de la formula empleando s() para especificar las componentes “suaves” (ver help(s) y Sección 7.3.3).

Algunas posibilidades de uso son las que siguen:

Modelo lineal⁶⁵:
```
ajuste <- gam(y ~ x1 + x2 + x3)
```
Modelo (semiparamétrico) aditivo con efectos no paramétricos para x1 y x2, y un efecto lineal para x3:
```
ajuste <- gam(y ~ s(x1) + s(x2) + x3)
```
Modelo no aditivo (con interacción):
```
ajuste <- gam(y ~ s(x1, x2))
```
Modelo (semiparamétrico) con distintas combinaciones :
```
ajuste <- gam(y ~ s(x1, x2) + s(x3) + x4)
```

En esta sección utilizaremos como ejemplo el conjunto de datos Prestige de la librería carData, considerando también el total de las observaciones (solo tiene 102) como si fuese la muestra de entrenamiento. Se tratará de explicar prestige (puntuación de ocupaciones obtenidas a partir de una encuesta) a partir de income (media de ingresos en la ocupación) y education (media de los años de educación).

library(mgcv)
data(Prestige, package = "carData")
modelo <- gam(prestige ~ s(income) + s(education), data = Prestige)
summary(modelo)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## prestige ~ s(income) + s(education)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   46.833      0.689      68   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df    F p-value    
## s(income)    3.12   3.88 14.6  <2e-16 ***
## s(education) 3.18   3.95 38.8  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.836   Deviance explained = 84.7%
## GCV = 52.143  Scale est. = 48.414    n = 102

En este caso, el método plot() representa los efectos (parciales) estimados de cada predictor (ver Figura 7.9):

plot(modelo, shade = TRUE, pages = 1) # residuals = FALSE por defecto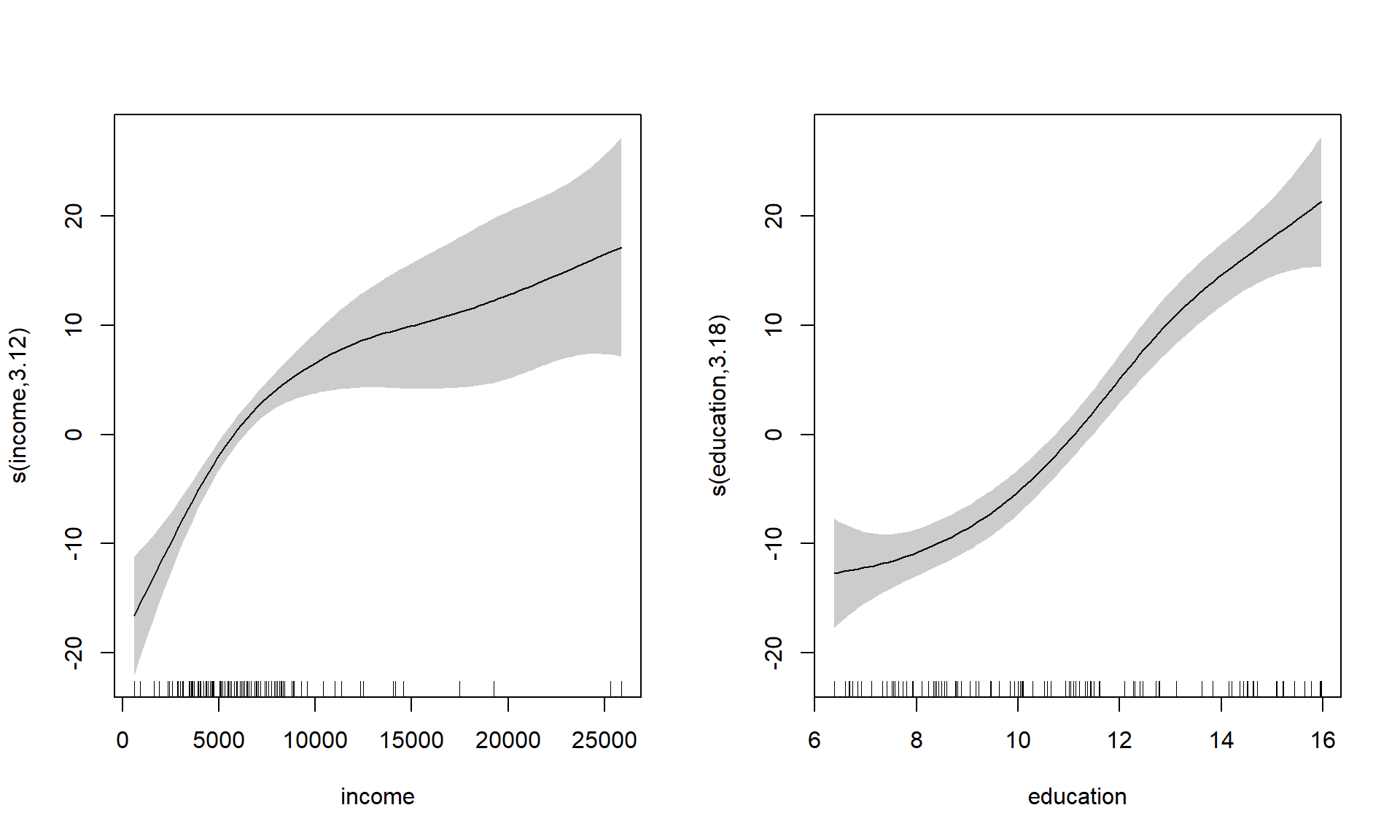

Figura 7.9: Estimaciones de los efectos parciales de income (izquierda) y education (derecha).

Por defecto, se representa cada componente no paramétrica (salvo que se especifique all.terms = TRUE), incluyendo gráficos de contorno para el caso de componentes bivariantes (correspondientes a interacciones entre predictores).

Se dispone también de un método predict() para calcular las predicciones de la forma habitual: por defecto devuelve las correspondientes a las observaciones modelo$fitted.values, y para nuevos datos hay que emplear el argumento newdata.

7.3.1 Superficies de predicción

En el caso bivariante, para representar las estimaciones (la superficie de predicción) obtenidas con el modelo se pueden utilizar las funciones persp() o versiones mejoradas como plot3D::persp3D(). Estas funciones requieren que los valores de entrada estén dispuestos en una rejilla bidimensional. Para generar esta rejilla se puede emplear la función expand.grid(x,y) que crea todas las combinaciones de los puntos dados en x e y (ver Figura 7.10):

inc <- with(Prestige, seq(min(income), max(income), len = 25))
ed <- with(Prestige, seq(min(education), max(education), len = 25))
newdata <- expand.grid(income = inc, education = ed)
# Representar
plot(income ~ education, Prestige, pch = 16)
abline(h = inc, v = ed, col = "grey")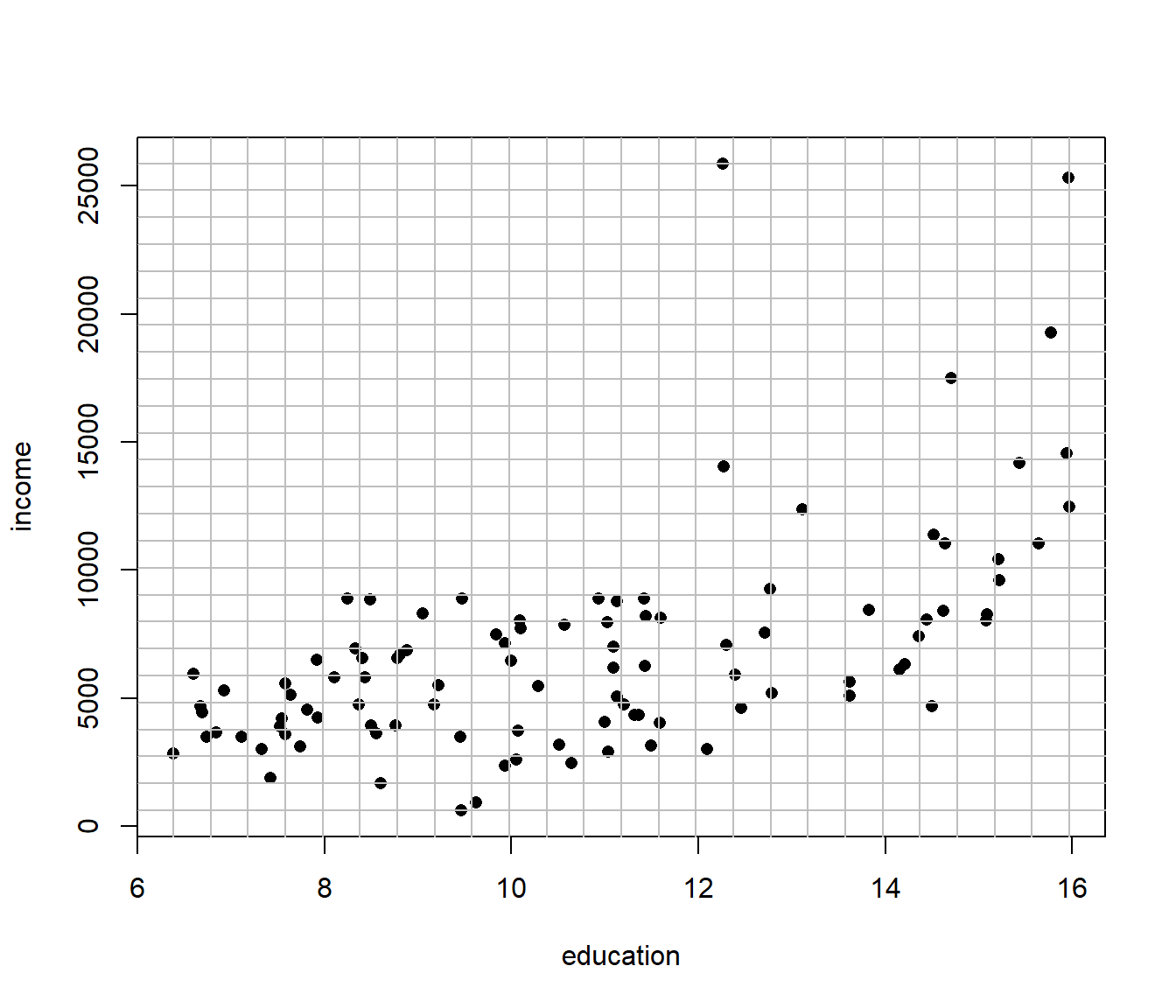

Figura 7.10: Observaciones y rejilla de predicción (para los predictores education e income).

A continuación, usamos estos valores para obtener la superficie de predicción, que en este caso representamos con la función plot3D::persp3D() (ver Figura 7.11). Alternativamente, se podrían emplear las funciones contour(), filled.contour(), plot3D::image2D() o similares.

pred <- predict(modelo, newdata)
pred <- matrix(pred, nrow = 25)
plot3D::persp3D(inc, ed, pred, theta = -40, phi = 30, ticktype = "detailed",
                xlab = "Income", ylab = "Education", zlab = "Prestige")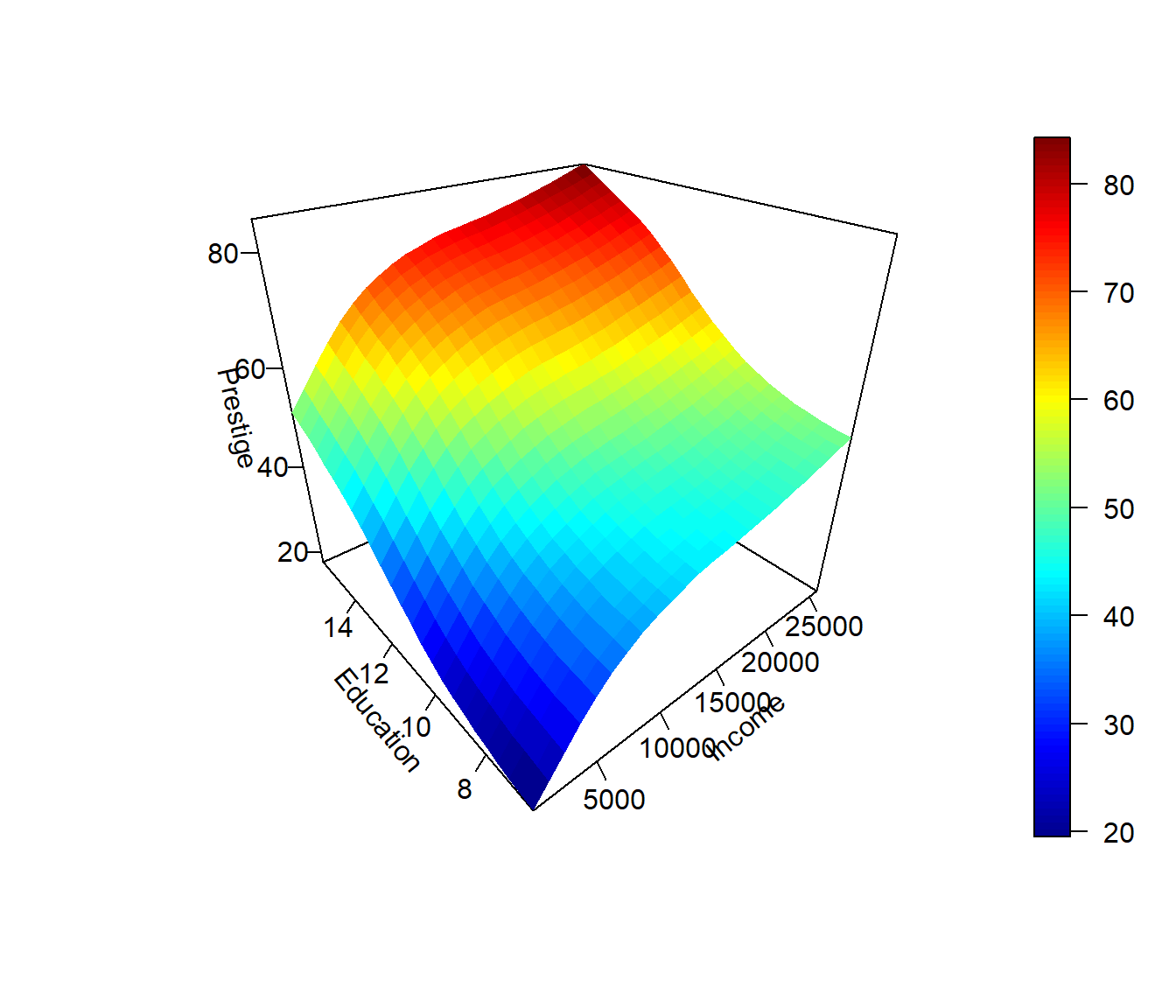

Figura 7.11: Superficie de predicción obtenida con el modelo GAM.

Otra posibilidad, quizás más cómoda, es utilizar el paquete modelr, que emplea gráficos ggplot2, para trabajar con modelos y predicciones.

7.3.2 Comparación y selección de modelos

Además de las medidas de bondad de ajuste, como el coeficiente de determinación ajustado, también se puede emplear la función anova() para la comparación de modelos (y seleccionar las componentes por pasos de forma interactiva). Por ejemplo, viendo la representación de los efectos (Figura 7.9 anterior) se podría pensar que el efecto de education podría ser lineal:

# plot(modelo)
modelo0 <- gam(prestige ~ s(income) + education, data = Prestige)
summary(modelo0)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## prestige ~ s(income) + education
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    4.224      3.732    1.13     0.26    
## education      3.968      0.341   11.63   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##            edf Ref.df    F p-value    
## s(income) 3.58   4.44 13.6  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.825   Deviance explained = 83.3%
## GCV = 54.798  Scale est. = 51.8      n = 102

anova(modelo0, modelo, test="F")

## Analysis of Deviance Table
## 
## Model 1: prestige ~ s(income) + education
## Model 2: prestige ~ s(income) + s(education)
##   Resid. Df Resid. Dev   Df Deviance    F Pr(>F)  
## 1      95.6       4995                            
## 2      93.2       4585 2.39      410 3.54  0.026 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este caso aceptaríamos que el modelo original es significativamente mejor.

Alternativamente, podríamos pensar que hay interacción:

modelo2 <- gam(prestige ~ s(income, education), data = Prestige)
summary(modelo2)

## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## prestige ~ s(income, education)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   46.833      0.714    65.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                      edf Ref.df    F p-value    
## s(income,education) 4.94    6.3 75.4  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.824   Deviance explained = 83.3%
## GCV = 55.188  Scale est. = 51.974    n = 102

En este caso, el coeficiente de determinación ajustado es menor y ya no tendría sentido realizar el contraste.

Además, se pueden seleccionar componentes del modelo (mediante regularización) empleando el parámetro select = TRUE. Para más detalles, consultar la ayuda help(gam.selection) o ejecutar example(gam.selection).

7.3.3 Diagnosis del modelo

La función gam.check() realiza una diagnosis descriptiva y gráfica del modelo ajustado (ver Figura 7.12):

gam.check(modelo)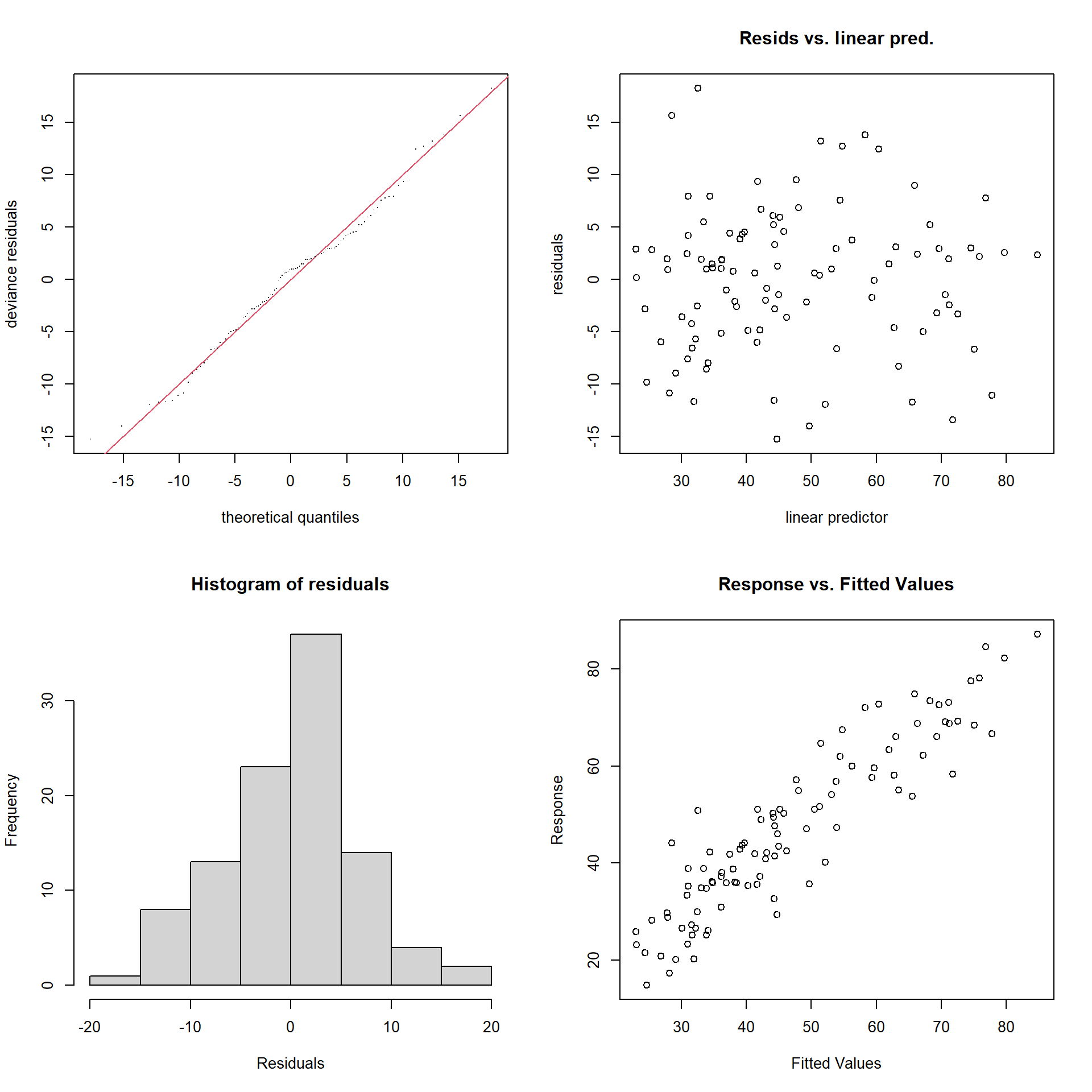

Figura 7.12: Gráficas de diagnóstico del modelo aditivo ajustado.

## 
## Method: GCV   Optimizer: magic
## Smoothing parameter selection converged after 4 iterations.
## The RMS GCV score gradient at convergence was 9.7839e-05 .
## The Hessian was positive definite.
## Model rank =  19 / 19 
## 
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
## 
##                k'  edf k-index p-value
## s(income)    9.00 3.12    0.98    0.32
## s(education) 9.00 3.18    1.03    0.60

Lo ideal sería observar normalidad en los dos gráficos de la izquierda, falta de patrón en el superior derecho, y ajuste a una recta en el inferior derecho. En este caso parece que el modelo se comporta adecuadamente. Como se deduce del resultado anterior, podría ser recomendable modificar la dimensión k de la base utilizada para construir la componente no paramétrica. Este valor se puede interpretar como el grado máximo de libertad permitido en esa componente. Normalmente no influye demasiado en el resultado, aunque puede influir en el tiempo de computación.

También se puede chequear la concurvidad (generalización de la colinealidad) entre las componentes del modelo, con la función concurvity():

concurvity(modelo)

##                para s(income) s(education)
## worst    3.0612e-23   0.59315      0.59315
## observed 3.0612e-23   0.40654      0.43986
## estimate 3.0612e-23   0.36137      0.40523

Esta función devuelve tres medidas por componente, que tratan de medir la proporción de variación de esa componente que está contenida en el resto (similares al complementario de la tolerancia). Un valor próximo a 1 indicaría que puede haber problemas de concurvidad.

También se pueden ajustar modelos GAM empleando caret. Por ejemplo, con los métodos "gam" y "gamLoess":

library(caret)
# names(getModelInfo("gam")) # 4 métodos
modelLookup("gam")

##   model parameter             label forReg forClass probModel
## 1   gam    select Feature Selection   TRUE     TRUE      TRUE
## 2   gam    method            Method   TRUE     TRUE      TRUE

modelLookup("gamLoess")

##      model parameter  label forReg forClass probModel
## 1 gamLoess      span   Span   TRUE     TRUE      TRUE
## 2 gamLoess    degree Degree   TRUE     TRUE      TRUE

Ejercicio 7.3 Continuando con los datos de MASS:mcycle, emplea mgcv::gam() para ajustar un spline penalizado para predecir accel a partir de times con las opciones por defecto y representa el ajuste. Compara el ajuste con el obtenido empleando un spline penalizado adaptativo (bs="ad"; ver ?adaptive.smooth).

Ejercicio 7.4 Empleando el conjunto de datos airquality, crea una muestra de entrenamiento y otra de test, y busca un modelo aditivo que resulte adecuado para explicar sqrt(Ozone) a partir de Temp, Wind y Solar.R. ¿Es preferible suponer que hay una interacción entre Temp y Wind?

Bibliografía

Hastie, T., y Tibshirani, R. (1990). Generalized Additive Models. Chapman; Hall. https://doi.org/10.1201/9780203753781

Wood, S. N. (2017). Generalized Additive Models: An Introduction with R (2a. ed.). Chapman & Hall/CRC.

No admite una fórmula del tipo respuesta ~ . (producirá un error). Habría que escribir la expresión explícita de la fórmula, por ejemplo con la ayuda de reformulate().↩︎