4.3 Bagging y bosques aleatorios en R

Estos algoritmos son de los más populares en AE y están implementados en numerosos paquetes de R, aunque la referencia es el paquete randomForest (Liaw y Wiener, 2002), que emplea el código Fortran desarrollado por Leo Breiman y Adele Cutler. La función principal es randomForest() y se suele emplear de la forma:

randomForest(formula, data, ntree, mtry, nodesize, ...)

formula y data (opcional): permiten especificar la respuesta y las variables predictoras de la forma habitual (típicamente respuesta ~ .), aunque si el conjunto de datos es muy grande puede ser preferible emplear una matriz o un data.frame para establecer los predictores y un vector para la respuesta (sustituyendo estos argumentos por x e y). Si la variable respuesta es un factor asumirá que se trata de un problema de clasificación, y en caso contrario de regresión.
ntree: número de árboles que se crecerán; por defecto 500.
mtry: número de predictores seleccionados al azar en cada división; por defecto max(floor(p/3), 1) en el caso de regresión y floor(sqrt(p)) en clasificación, siendo p = ncol(x) = ncol(data) - 1 el número de predictores.
nodesize: número mínimo de observaciones en un nodo terminal; por defecto 1 en clasificación y 5 en regresión. Si el conjunto de datos es muy grande, es recomendable incrementarlo para evitar problemas de sobreajuste, disminuir el tiempo de computación y los requerimientos de memoria. Puede ser tratado como un hiperparámetro.

Otros argumentos que pueden ser de interés⁴³ son:

maxnodes: número máximo de nodos terminales. Puede utilizarse como alternativa para controlar la complejidad del modelo.
importance = TRUE: permite obtener medidas adicionales de la importancia de las variables predictoras.
proximity = TRUE: permite obtener una matriz de proximidades (componente $proximity) entre las observaciones (frecuencia con la que los pares de observaciones están en el mismo nodo terminal).
na.action = na.fail: por defecto, no admite datos faltantes con la interfaz de fórmulas. Si los hubiese, se podrían imputar estableciendo na.action = na.roughfix (empleando medias o modas) o llamando previamente a rfImpute() (que emplea proximidades obtenidas con un bosque aleatorio).

Para obtener más información, puede consultarse la documentación de la función y Liaw y Wiener (2002).

Entre las numerosas alternativas disponibles, además de las implementadas en paquetes que integran colecciones de métodos como h2o o RWeka, una de las más utilizadas son los bosques aleatorios con conditional inference trees, implementada en la función cforest() del paquete party.

4.3.1 Ejemplo: clasificación con bagging

Como ejemplo consideraremos el conjunto de datos de calidad de vino empleado previamente en la Sección 3.3.2, y haremos comparaciones con el ajuste de un único árbol.

data(winetaste, package = "mpae")
set.seed(1)
df <- winetaste
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

Al ser bagging con árboles un caso particular de bosques aleatorios, cuando $m = p$, también podemos emplear randomForest:

library(randomForest)
set.seed(4) # NOTA: Fijamos esta semilla para ilustrar dependencia
bagtrees <- randomForest(taste ~ ., data = train, mtry = ncol(train) - 1)
bagtrees

## 
## Call:
##  randomForest(formula = taste ~ ., data = train, mtry = ncol(train) -      1) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 11
## 
##         OOB estimate of  error rate: 23.5%
## Confusion matrix:
##      good bad class.error
## good  565  97     0.14653
## bad   138 200     0.40828

Con el método plot() podemos examinar la convergencia del error en las muestras OOB. Este método emplea matplot() para representar la componente $err.rate, como se muestra en la Figura 4.1:

plot(bagtrees, main = "")
legend("right", colnames(bagtrees$err.rate), lty = 1:5, col = 1:6)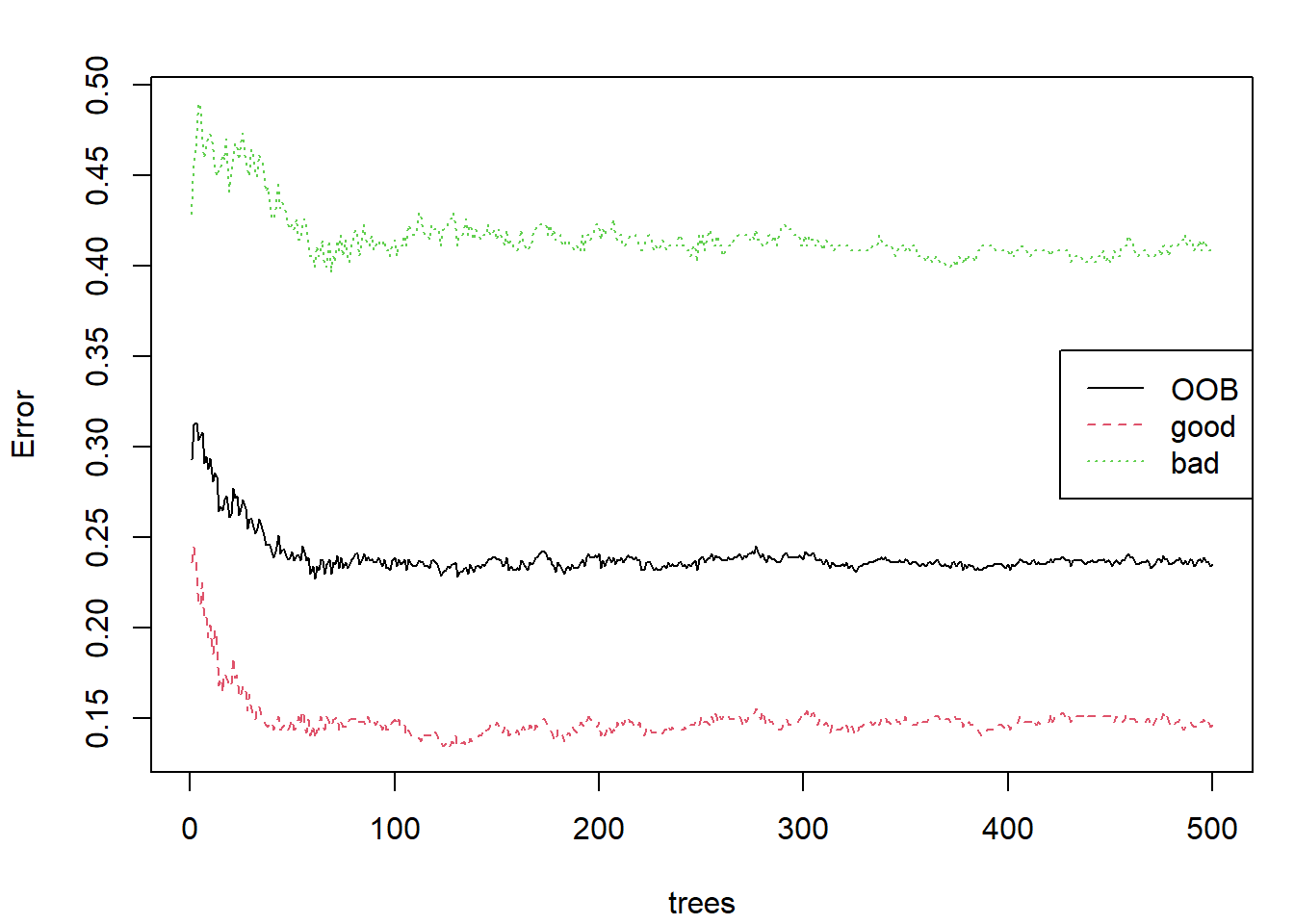

Figura 4.1: Evolución de las tasas de error OOB al emplear bagging para la predicción de winetaste$taste.

Como se observa, los errores tienden a estabilizarse, lo que sugiere que hay convergencia en el proceso (aunque situaciones de alta dependencia entre los árboles dificultarían su interpretación).

Con la función getTree() podemos extraer los árboles individuales. Por ejemplo, el siguiente código permite extraer la variable seleccionada para la primera división:

split_var_1 <- sapply(seq_len(bagtrees$ntree), function(i) 
                       getTree(bagtrees, i, labelVar = TRUE)[1, "split var"])

En este caso concreto, podemos observar que la variable seleccionada para la primera división es siempre la misma, lo que indicaría una alta dependencia entre los distintos árboles:

table(split_var_1)

## split_var_1
##              alcohol            chlorides          citric.acid 
##                  500                    0                    0 
##              density        fixed.acidity  free.sulfur.dioxide 
##                    0                    0                    0 
##                   pH       residual.sugar            sulphates 
##                    0                    0                    0 
## total.sulfur.dioxide     volatile.acidity 
##                    0                    0

Por último, evaluamos la precisión en la muestra de test:

pred <- predict(bagtrees, newdata = test)
caret::confusionMatrix(pred, test$taste)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction good bad
##       good  145  42
##       bad    21  42
##                                         
##                Accuracy : 0.748         
##                  95% CI : (0.689, 0.801)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 0.00254       
##                                         
##                   Kappa : 0.398         
##                                         
##  Mcnemar's Test P-Value : 0.01174       
##                                         
##             Sensitivity : 0.873         
##             Specificity : 0.500         
##          Pos Pred Value : 0.775         
##          Neg Pred Value : 0.667         
##              Prevalence : 0.664         
##          Detection Rate : 0.580         
##    Detection Prevalence : 0.748         
##       Balanced Accuracy : 0.687         
##                                         
##        'Positive' Class : good          
##

4.3.2 Ejemplo: clasificación con bosques aleatorios

Continuando con el ejemplo anterior, empleamos la función randomForest() con las opciones por defecto para ajustar un bosque aleatorio a la muestra de entrenamiento:

set.seed(1)
rf <- randomForest(taste ~ ., data = train)
rf

## 
## Call:
##  randomForest(formula = taste ~ ., data = train) 
##                Type of random forest: classification
##                      Number of trees: 500
## No. of variables tried at each split: 3
## 
##         OOB estimate of  error rate: 22%
## Confusion matrix:
##      good bad class.error
## good  578  84     0.12689
## bad   136 202     0.40237

En la Figura 4.2 podemos observar que aparentemente hay convergencia, igual que sucedía en el ejemplo anterior, y por tanto tampoco sería necesario aumentar el número de árboles.

plot(rf, main = "")
legend("right", colnames(rf$err.rate), lty = 1:5, col = 1:6)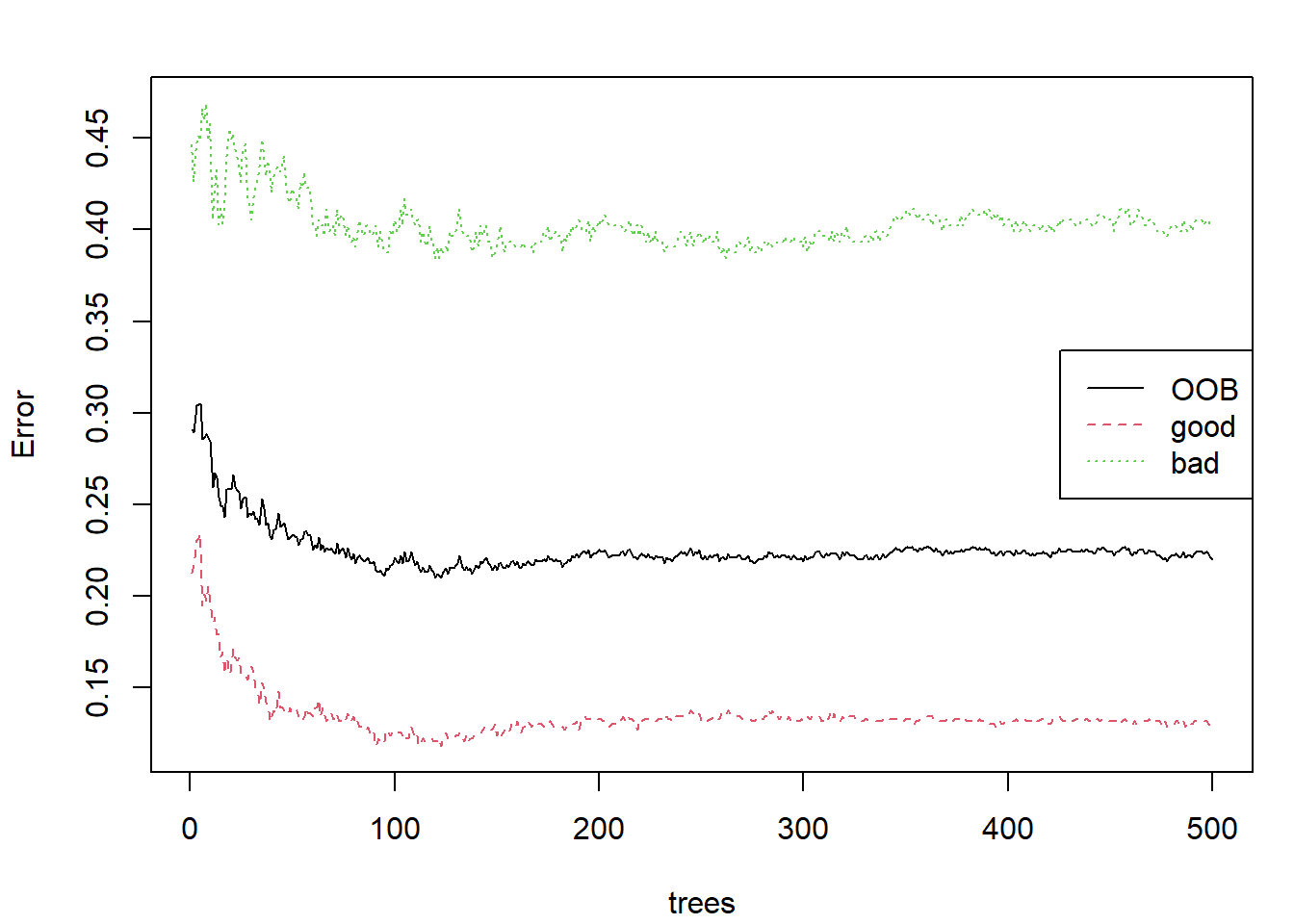

Evolución de las tasas de error OOB al usar bosques aleatorios para la predicción de winetaste$taste (empleando randomForest() con las opciones por defecto).

Figura 4.2: Evolución de las tasas de error OOB al usar bosques aleatorios para la predicción de winetaste$taste (empleando randomForest() con las opciones por defecto).

Podemos mostrar la importancia de las variables predictoras (utilizadas en el bosque aleatorio y sus sustitutas) con la función importance() o representarlas con varImpPlot() (ver Figura 4.3):

importance(rf)

##                      MeanDecreaseGini
## fixed.acidity                  37.772
## volatile.acidity               43.998
## citric.acid                    41.501
## residual.sugar                 36.799
## chlorides                      33.621
## free.sulfur.dioxide            42.291
## total.sulfur.dioxide           39.637
## density                        45.387
## pH                             32.314
## sulphates                      30.323
## alcohol                        63.892

varImpPlot(rf)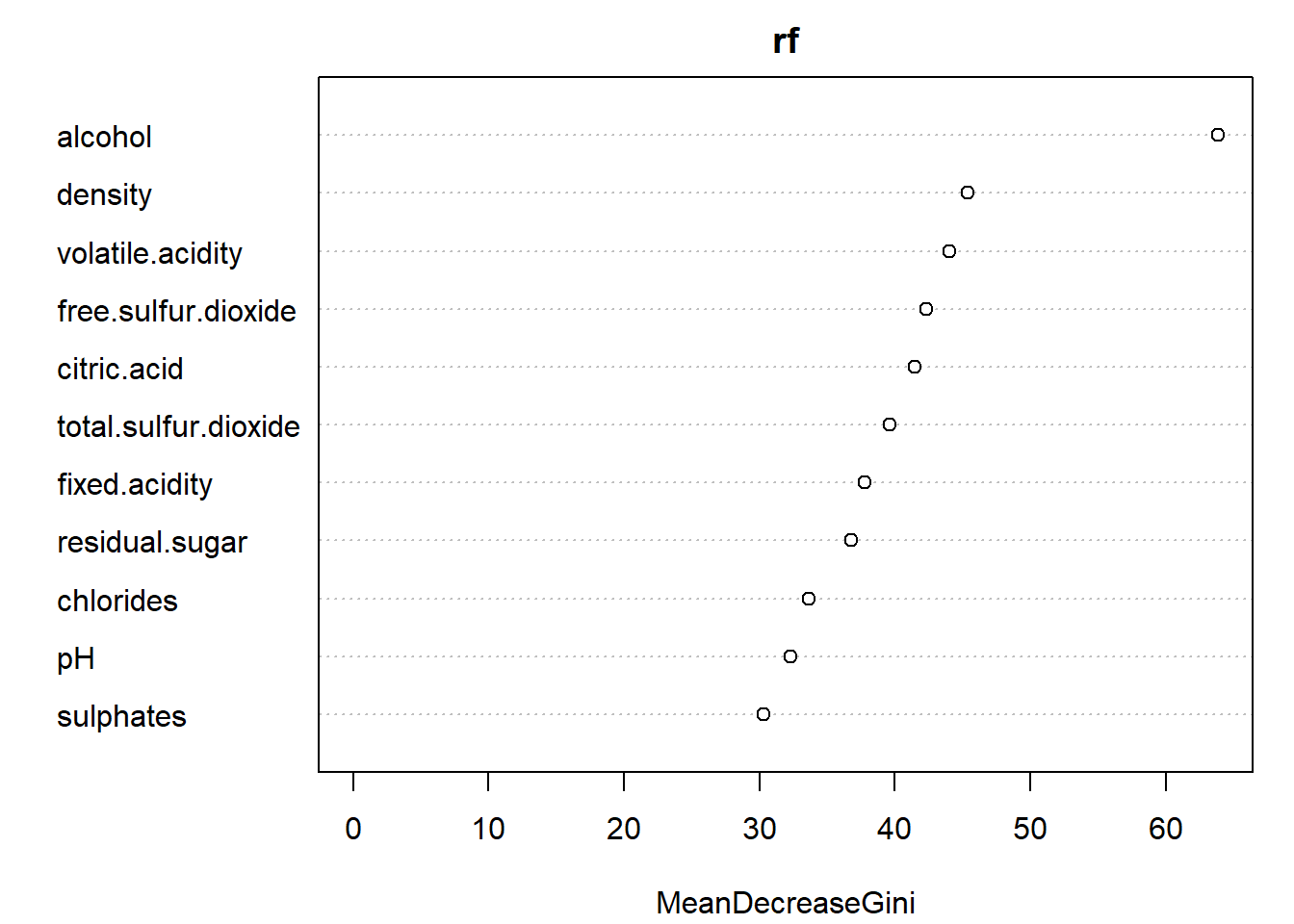

Figura 4.3: Importancia de las variables predictoras al emplear bosques aleatorios para la predicción de winetaste$taste.

Si evaluamos la precisión en la muestra de test podemos observar un ligero incremento en la precisión en comparación con el método anterior:

pred <- predict(rf, newdata = test)
caret::confusionMatrix(pred, test$taste)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction good bad
##       good  153  43
##       bad    13  41
##                                         
##                Accuracy : 0.776         
##                  95% CI : (0.719, 0.826)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 7.23e-05      
##                                         
##                   Kappa : 0.449         
##                                         
##  Mcnemar's Test P-Value : 0.000106      
##                                         
##             Sensitivity : 0.922         
##             Specificity : 0.488         
##          Pos Pred Value : 0.781         
##          Neg Pred Value : 0.759         
##              Prevalence : 0.664         
##          Detection Rate : 0.612         
##    Detection Prevalence : 0.784         
##       Balanced Accuracy : 0.705         
##                                         
##        'Positive' Class : good          
##

Esta mejora sería debida a que en este caso la dependencia entre los árboles es menor:

split_var_1 <- sapply(seq_len(bagtrees$ntree), function(i) 
                       getTree(bagtrees, i, labelVar = TRUE)[1, "split var"])
table(split_var_1)

## split_var_1
##              alcohol            chlorides          citric.acid 
##                  500                    0                    0 
##              density        fixed.acidity  free.sulfur.dioxide 
##                    0                    0                    0 
##                   pH       residual.sugar            sulphates 
##                    0                    0                    0 
## total.sulfur.dioxide     volatile.acidity 
##                    0                    0

El análisis e interpretación del modelo puede resultar más complicado en este tipo de métodos. Para estudiar el efecto de los predictores en la respuesta se suelen emplear algunas de las herramientas descritas en la Sección 1.5. Por ejemplo, empleando la función pdp::partial() (B. M. Greenwell, 2022) podemos generar gráficos PDP con las estimaciones de los efectos individuales de los principales predictores (ver Figura 4.4):

library(pdp)
library(gridExtra)
pdp1 <- partial(rf, "alcohol")
p1 <- plotPartial(pdp1)
pdp2 <- partial(rf, c("density"))
p2 <- plotPartial(pdp2)
grid.arrange(p1, p2, ncol = 2)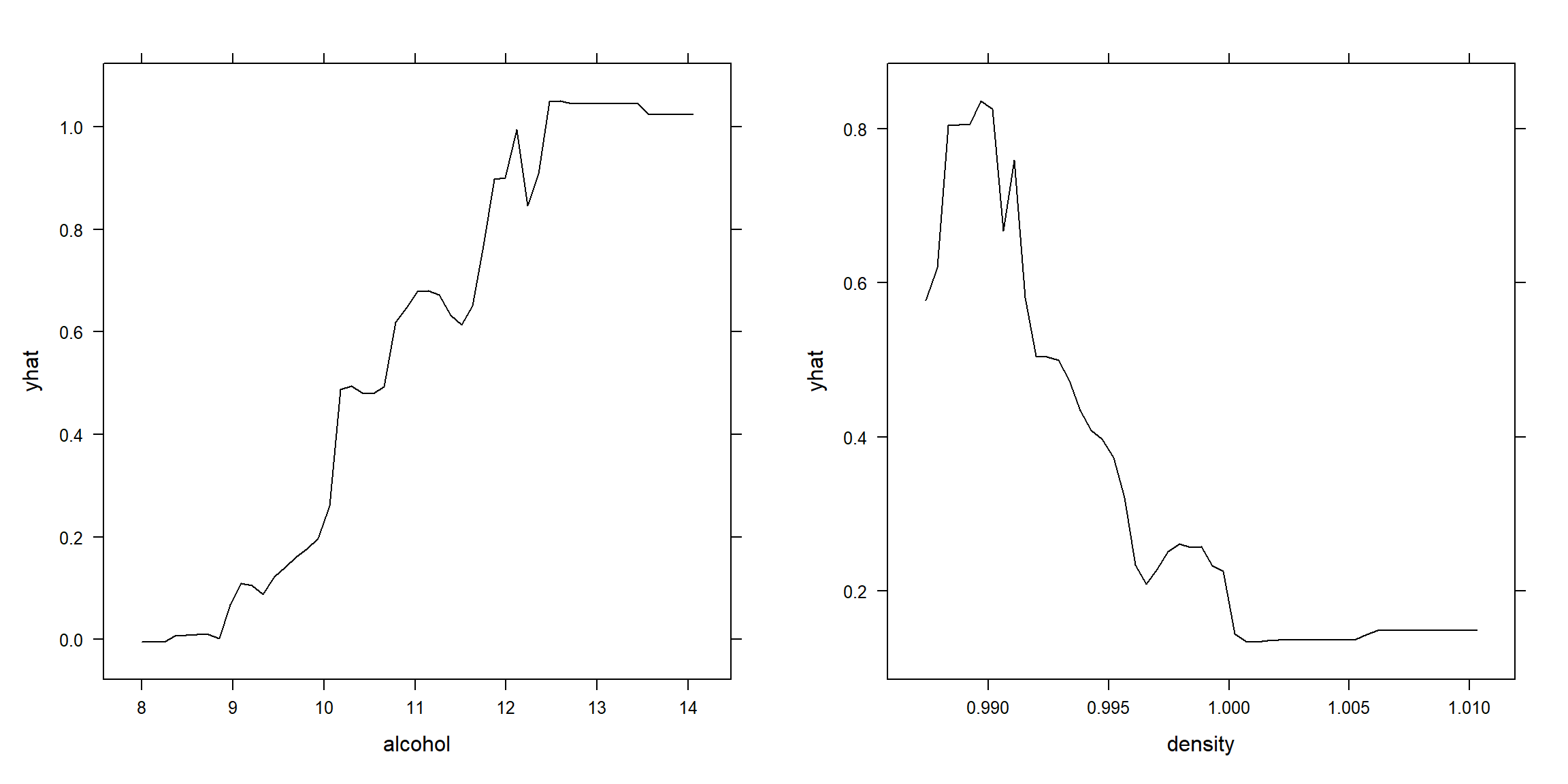

Figura 4.4: Efecto parcial del alcohol (panel izquierdo) y la densidad (panel derecho) sobre la respuesta.

Adicionalmente, estableciendo ice = TRUE se calculan las curvas de expectativa condicional individual (ICE). Estos gráficos ICE extienden los PDP, ya que, además de mostrar la variación del promedio (línea roja en Figura 4.5), también muestra la variación de los valores predichos para cada observación (líneas negras en Figura 4.5).

ice1 <- partial(rf, pred.var = "alcohol", ice = TRUE)
ice2 <- partial(rf, pred.var = "density", ice = TRUE)
p1 <- plotPartial(ice1, alpha = 0.5)
p2 <- plotPartial(ice2, alpha = 0.5)
gridExtra:::grid.arrange(p1, p2, ncol = 2)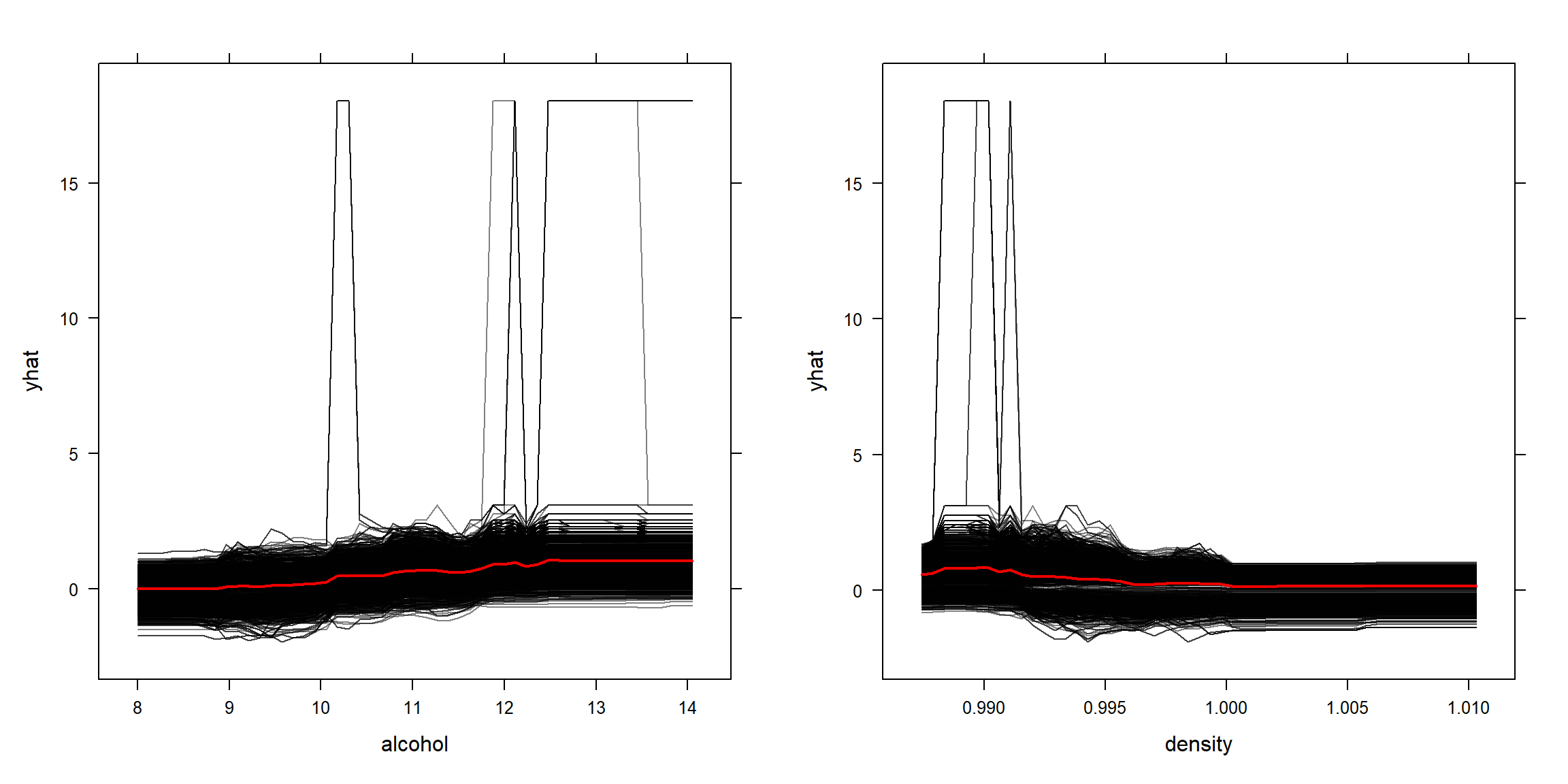

Figura 4.5: Efecto individual de cada observación de alcohol (panel izquierdo) y densidad (panel derecho) sobre la respuesta.

Se pueden crear gráficos similares utilizando los otros paquetes indicados en la Sección 1.5. Por ejemplo, la Figura 4.6, generada con el paquete vivid (Inglis et al., 2023), muestra medidas de la importancia de los predictores (Vimp) en la diagonal y de la fuerza de las interacciones (Vint) fuera de la diagonal.

library(vivid)
fit_rf <- vivi(data = train, fit = rf, response = "taste", 
               importanceType = "%IncMSE")
viviHeatmap(mat = fit_rf[1:5,1:5])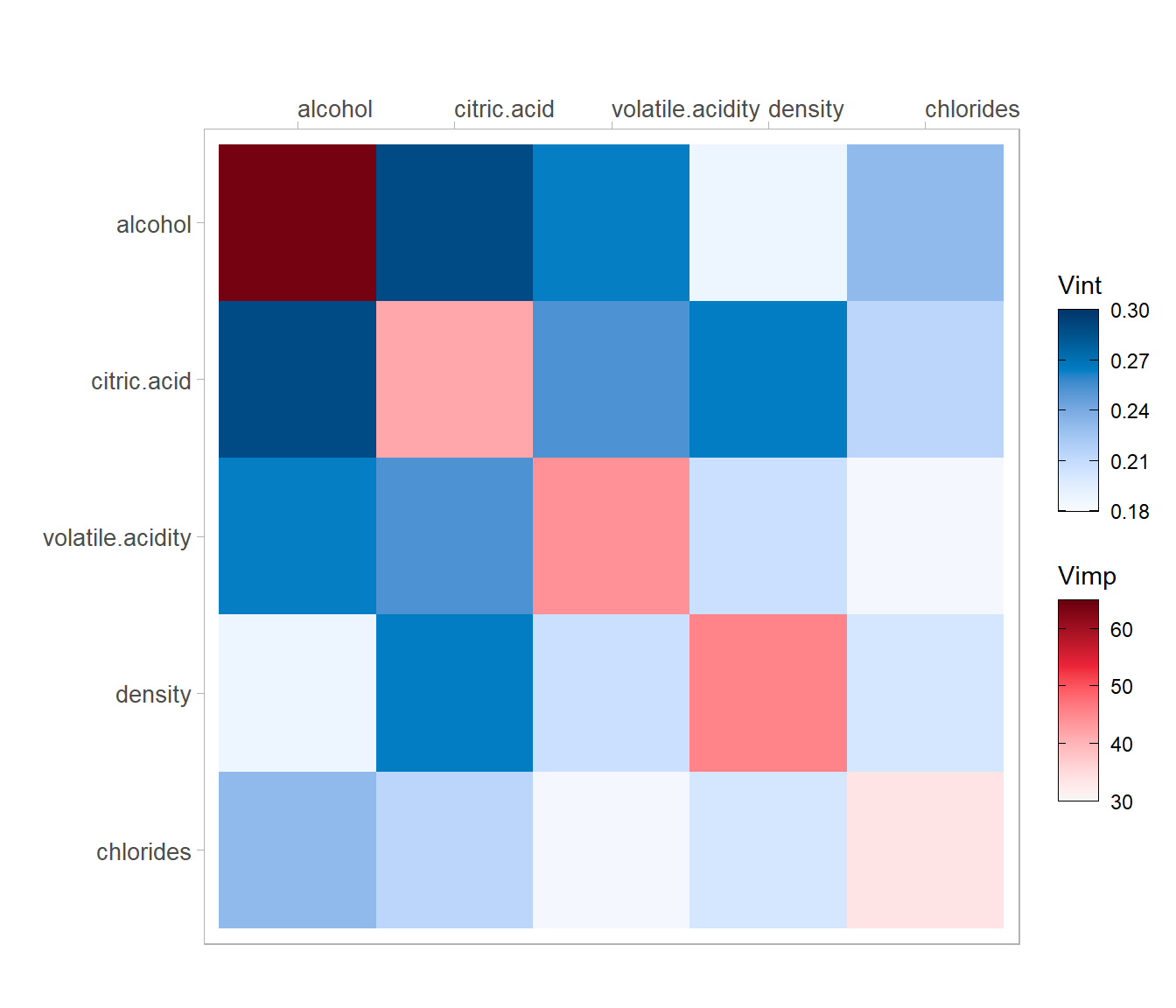

Figura 4.6: Mapa de calor de la importancia e interaciones de los predictores del ajuste mediante bosques aleatorios.

Alternativamente, también se pueden visualizar las relaciones mediante un gráfico de red (ver Figura 4.7).

require(igraph)
viviNetwork(mat = fit_rf)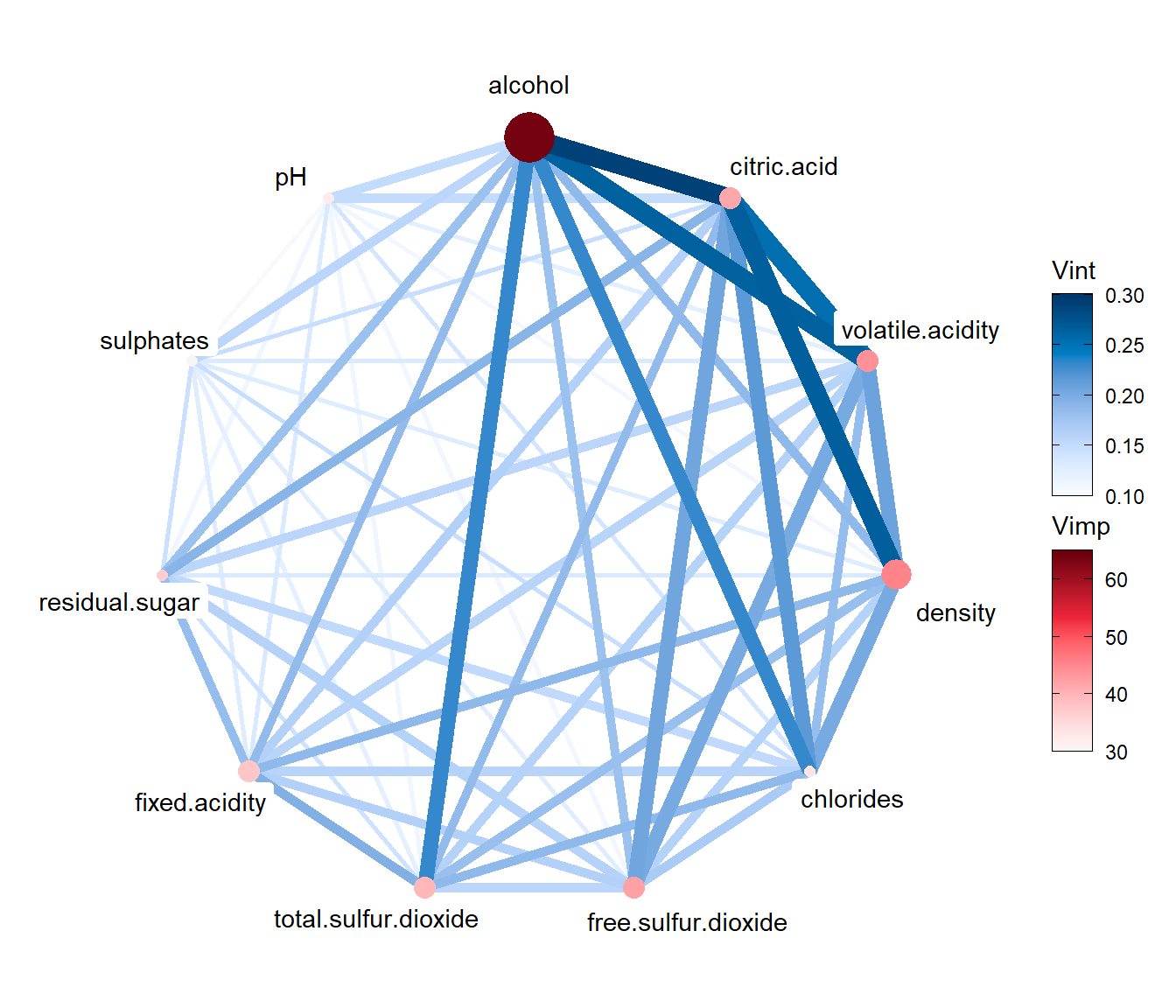

Figura 4.7: Gráfico de red para la importancia e interaciones del ajuste mediante bosques aleatorios.

En este caso, la interación entre alcohol y citric.acid es aparentemente la más importante. Podemos representarla mediante un gráfico PDP (ver Figura 4.8). La generación de este gráfico puede requerir mucho tiempo de computación.

pdp12 <- partial(rf, c("alcohol", "citric.acid"))
plotPartial(pdp12)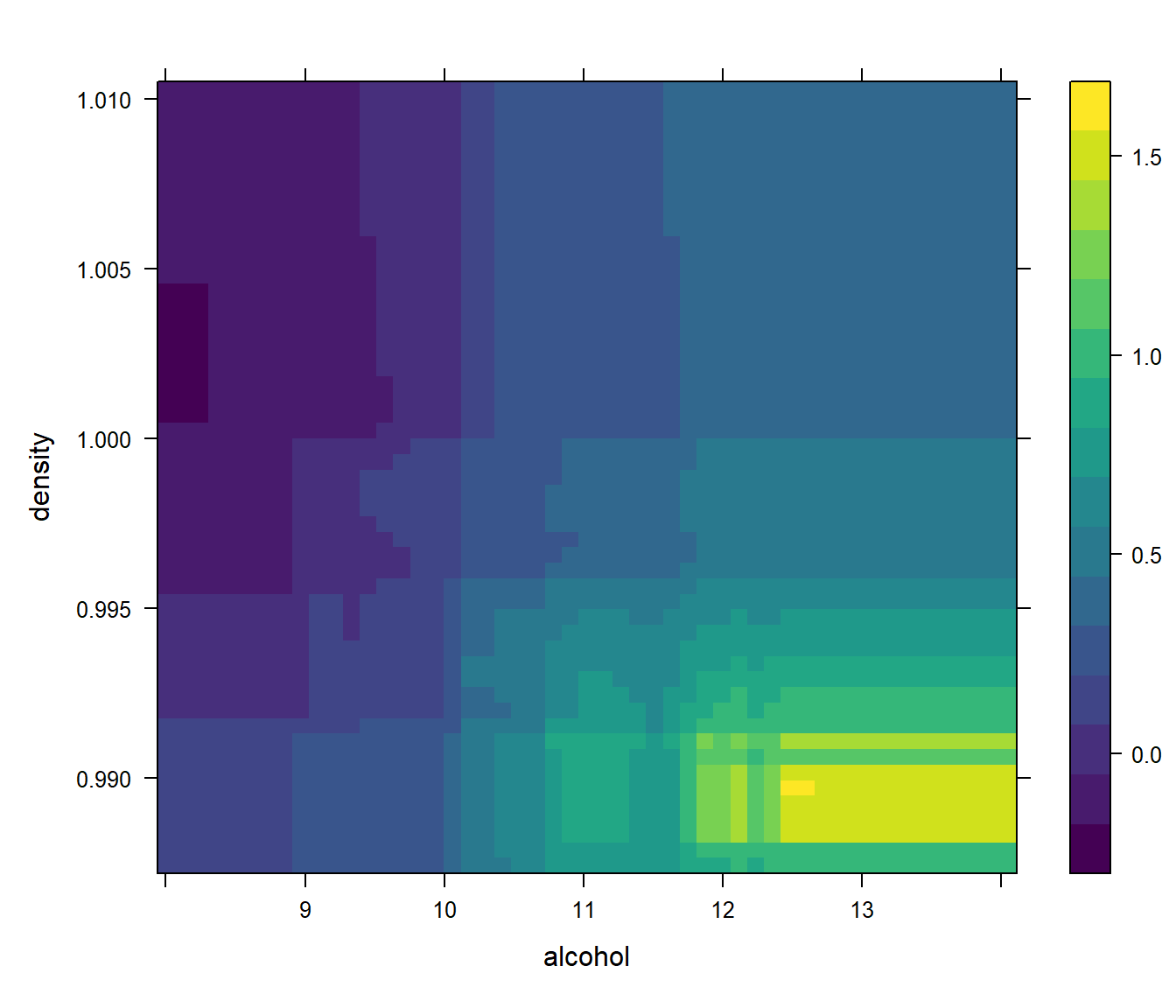

Figura 4.8: Efecto parcial de la interacción del alcohol y el ácido cítrico sobre la respuesta.

4.3.3 Ejemplo: bosques aleatorios con `caret`

En el paquete caret hay varias implementaciones de bagging y bosques aleatorios⁴⁴, incluyendo el algoritmo del paquete randomForest considerando como hiperparámetro el número de predictores seleccionados al azar en cada división, mtry. Para ajustar este modelo a una muestra de entrenamiento hay que establecer method = "rf" en la llamada a train().

library(caret)
# str(getModelInfo("rf", regex = FALSE))
modelLookup("rf")

##   model parameter                         label forReg forClass
## 1    rf      mtry #Randomly Selected Predictors   TRUE     TRUE
##   probModel
## 1      TRUE

Con las opciones por defecto únicamente evalúa tres valores posibles del hiperparámetro (ver Figura 4.9). Opcionalmente se podría aumentar el número de valores a evaluar con tuneLength o especificarlos directamente con tuneGrid. Sin embargo, el tiempo de computación puede ser demasiado alto, por lo que es recomendable reducir el valor de nodesize, paralelizar los cálculos o emplear otros paquetes con implementaciones más eficientes. Además, en este caso es preferible emplear el método por defecto para la selección de hiperparámetros, el remuestreo (que sería equivalente a trainControl(method = "oob")), para aprovechar los cálculos realizados durante la construcción de los modelos.

set.seed(1)
rf.caret <- train(taste ~ ., data = train, method = "rf")
ggplot(rf.caret, highlight = TRUE)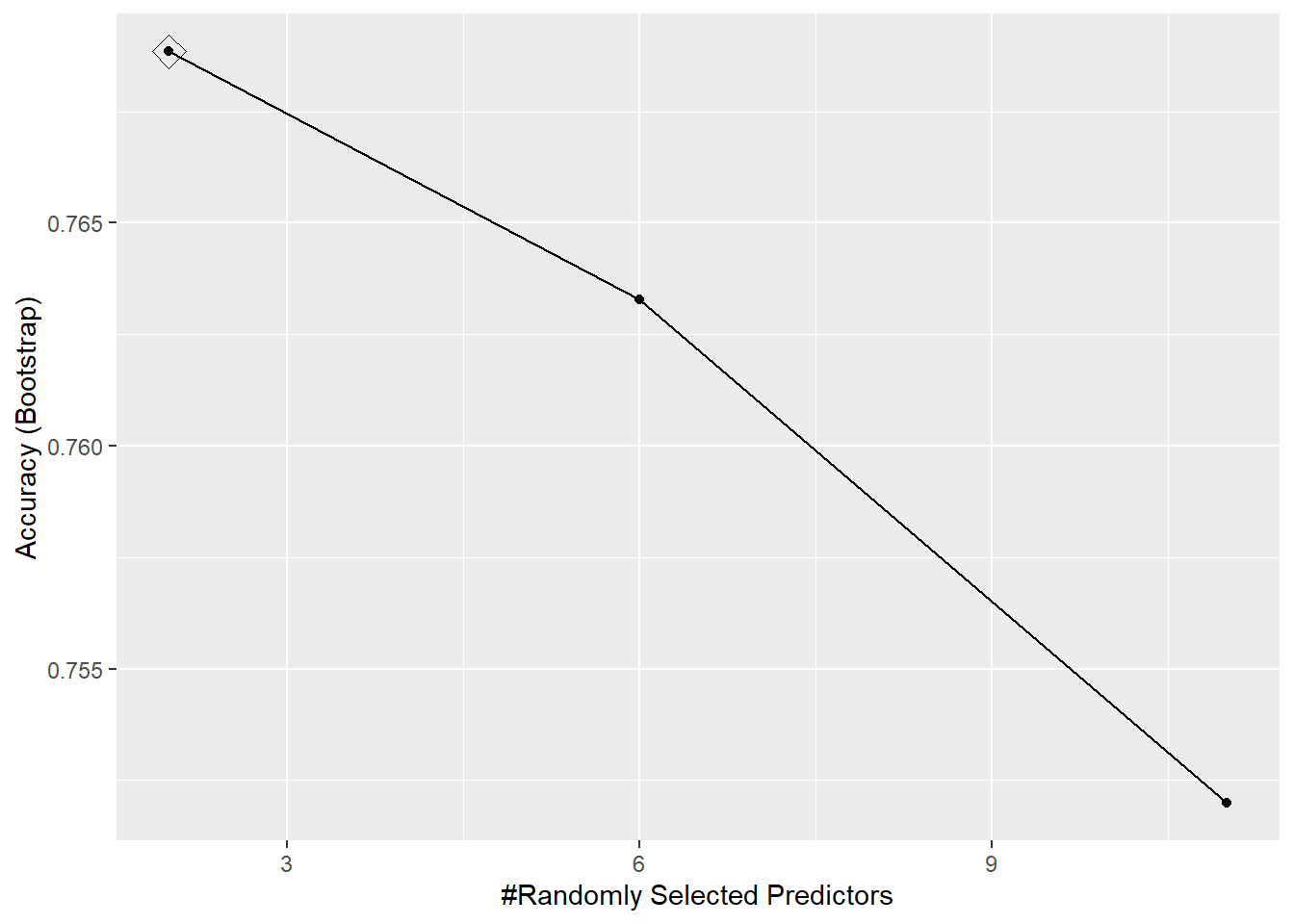

Figura 4.9: Evolución de la precisión de un bosque aleatorio dependiendo del número de predictores seleccionados.

Breiman (2001a) sugiere emplear el valor por defecto para mtry, así como la mitad y el doble de este valor (ver Figura 4.10).

mtry.class <- sqrt(ncol(train) - 1)
tuneGrid <- data.frame(mtry = 
                         floor(c(mtry.class/2, mtry.class, 2*mtry.class)))
set.seed(1)
rf.caret <- train(taste ~ ., data = train,
                  method = "rf", tuneGrid = tuneGrid)
ggplot(rf.caret, highlight = TRUE)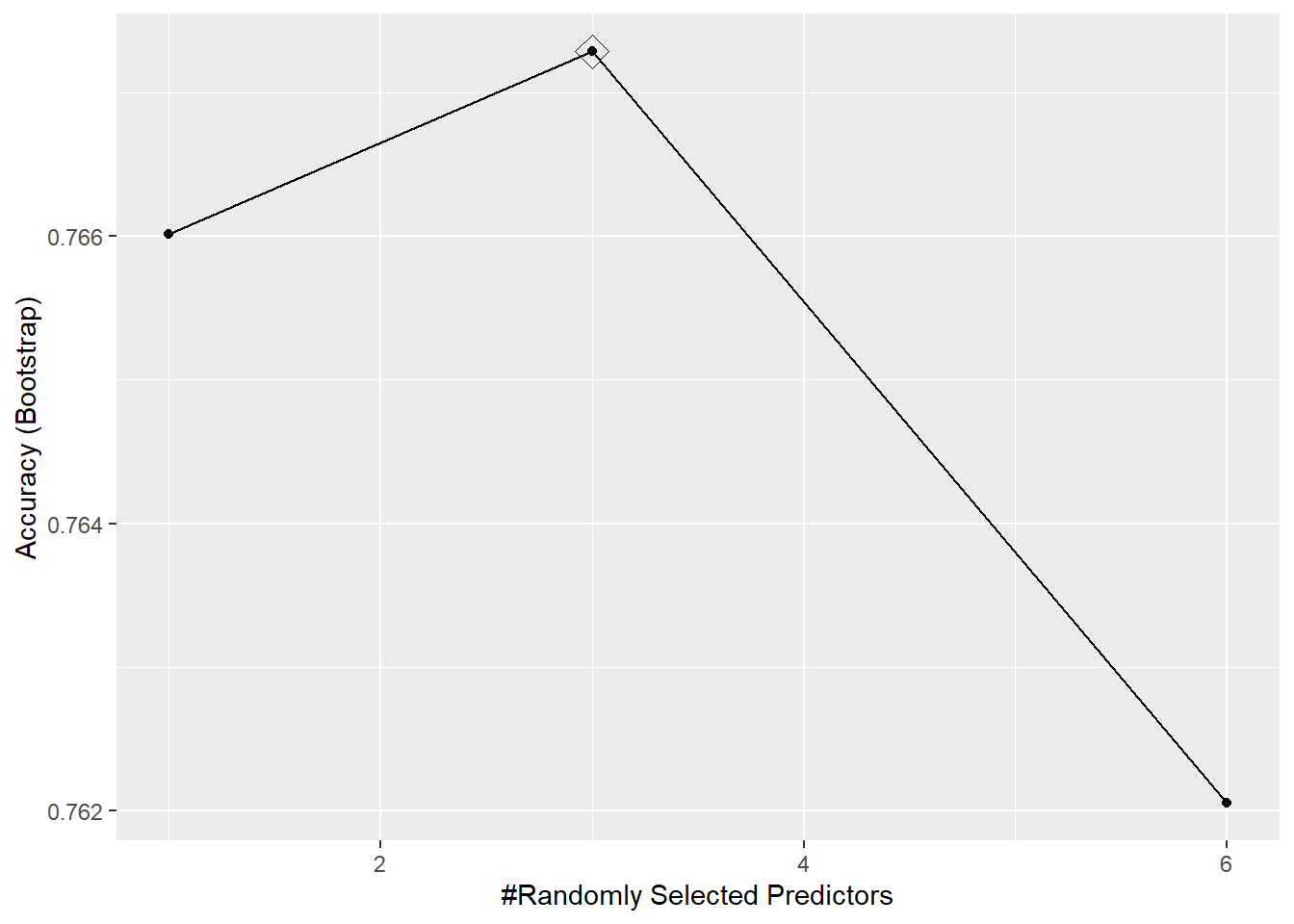

Figura 4.10: Evolución de la precisión de un bosque aleatorio con caret usando el argumento tuneGrid.

Ejercicio 4.1 Como acabamos de ver, caret permite ajustar un bosque aleatorio considerando mtry como único hiperparámetro, pero también nos podría interesar buscar valores adecuados para otros parámetros, como por ejemplo nodesize. Esto se puede realizar fácilmente empleando directamente la función randomForest(). En primer lugar, habría que construir la rejilla de búsqueda con las combinaciones de los valores de los hiperparámetros que se quieren evaluar (para ello se puede utilizar la función expand.grid()). Posteriormente, se ajustaría un bosque aleatorio en la muestra de entrenamiento con cada una de las combinaciones (por ejemplo utilizando un bucle for) y se emplearía el error OOB para seleccionar la combinación óptima (al que podemos acceder empleando with(fit, err.rate[ntree, "OOB"]), suponiendo que fit contiene el bosque aleatorio ajustado).

Continuando con el mismo conjunto de datos de calidad de vino, emplea la función randomForest() para ajustar un bosque aleatorio con el fin de clasificar la calidad del vino (taste), considerando 500 árboles y empleando el error OOB para seleccionar los valores “óptimos” de los hiperparámetros. Para ello, utiliza las posibles combinaciones de mtry = floor(c(mtry.class/2, mtry.class, 2*mtry.class)) (siendo mtry.class <- sqrt(ncol(train) - 1)) y nodesize = c(1, 3, 5, 10).

Ejercicio 4.2 Utilizando el conjunto de datos mpae::bfan, emplea el método "rf" del paquete caret para clasificar los individuos según su nivel de grasa corporal (bfan):

Particiona los datos, considerando un 80 % de las observaciones como muestra de aprendizaje y el 20 % restante como muestra de test.
Ajusta un bosque aleatorio con 300 árboles a los datos de entrenamiento, seleccionando el número de predictores empleados en cada división mtry = c(1, 2, 4, 6) mediante validación cruzada con 10 grupos y empleando el criterio de un error estándar de Breiman.
Estudia la convergencia del error en las muestras OOB.
Estudia la importancia de las variables. Estima el efecto individual del predictor más importante mediante un gráfico PDP e interpreta el resultado.
Evalúa la precisión de las predicciones en la muestra de test.

Bibliografía

Breiman, L. (2001a). Random forests. Machine Learning, 45(1), 5-32.

Greenwell, B. M. (2022). pdp: Partial Dependence Plots. https://cran.r-project.org/package=pdp

Inglis, A., Parnell, A., y Hurley, C. (2023). vivid: Variable Importance and Variable Interaction Displays. https://cran.r-project.org/package=vivid

Liaw, A., y Wiener, M. (2002). Classification and Regression by randomForest. R News, 2(3), 18-22. https://www.r-project.org/doc/Rnews/Rnews_2002-3.pdf

Si se quiere minimizar el uso de memoria, por ejemplo mientras se seleccionan hiperparámetros, se puede establecer keep.forest=FALSE.↩︎
Se puede hacer una búsqueda en la tabla del Capítulo 6: Available Models del manual.↩︎