4.5 Boosting en R

Los métodos boosting están entre los más populares en aprendizaje estadístico. Están implementados en numerosos paquetes de R, por ejemplo: ada, adabag, mboost, gbm, xgboost.

4.5.1 Ejemplo: clasificación con el paquete ada

La función ada() del paquete ada (Culp et al., 2006) implementa diversos métodos boosting, incluyendo el algoritmo original AdaBoost. Emplea rpart para la construcción de los árboles, aunque solo admite respuestas dicotómicas y dos funciones de pérdida (exponencial y logística). Además, un posible problema al emplear esta función es que ordena alfabéticamente los niveles del factor, lo que puede llevar a una mala interpretación de los resultados.

Los principales parámetros son los siguientes:

ada(formula, data, loss = c("exponential", "logistic"),
    type = c("discrete", "real", "gentle"), iter = 50, 
    nu = 0.1, bag.frac = 0.5, ...)

  • formula y data (opcional): permiten especificar la respuesta y las variables predictoras de la forma habitual (típicamente respuesta ~ .; también admite matrices x e y en lugar de fórmulas).

  • loss: función de pérdida; por defecto "exponential" (algoritmo AdaBoost).

  • type: algoritmo boosting; por defecto "discrete" que implementa el algoritmo AdaBoost original que predice la variable respuesta. Otras alternativas son "real", que implementa el algoritmo Real AdaBoost (Friedman et al., 2000) que permite estimar las probabilidades, y "gentle", una versión modificada del anterior que emplea un método Newton de optimización por pasos (en lugar de optimización exacta).

  • iter: número de iteraciones boosting; por defecto 50.

  • nu: parámetro de regularización \(\lambda\); por defecto 0.1. Disminuyendo este parámetro es de esperar que se obtenga una mejora en la precisión de las predicciones, pero requeriría aumentar iter, aumentando notablemente el tiempo de computación y los requerimientos de memoria.

  • bag.frac: proporción de observaciones seleccionadas al azar para crecer cada árbol; 0.5 por defecto.

  • ...: argumentos adicionales para rpart.control; por defecto rpart.control(maxdepth = 1, cp = -1, minsplit = 0, xval = 0).

A modo de ejemplo consideraremos el conjunto de datos de calidad de vino empleado en las secciones 3.3.2 y 4.3. Para evitar problemas reordenamos alfabéticamente los niveles de la respuesta.

# data(winetaste, package = "mpae")
# Reordenar alfabéticamente los niveles de winetaste$taste
winetaste$taste <- factor(as.character(winetaste$taste))
# Partición de los datos
set.seed(1)
df <- winetaste
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

El siguiente código llama a la función ada() con la opción para estimar probabilidades (type = "real", Real AdaBoost), considerando interacciones de segundo orden entre los predictores (maxdepth = 2), disminuyendo ligeramente el valor del parámetro de aprendizaje y aumentando el número de iteraciones:

library(ada)
control <- rpart.control(maxdepth = 2, cp = 0, minsplit = 10, xval = 0)
ada.boost <- ada(taste ~ ., data = train, type = "real",
             control = control, iter = 100, nu = 0.05)
ada.boost
## Call:
## ada(taste ~ ., data = train, type = "real", control = control, 
##     iter = 100, nu = 0.05)
## 
## Loss: exponential Method: real   Iteration: 100 
## 
## Final Confusion Matrix for Data:
##           Final Prediction
## True value bad good
##       bad  162  176
##       good  46  616
## 
## Train Error: 0.222 
## 
## Out-Of-Bag Error:  0.233  iteration= 99 
## 
## Additional Estimates of number of iterations:
## 
## train.err1 train.kap1 
##         93         93

Con el método plot() podemos representar la evolución del error de clasificación al aumentar el número de iteraciones (ver Figura 4.11):

plot(ada.boost)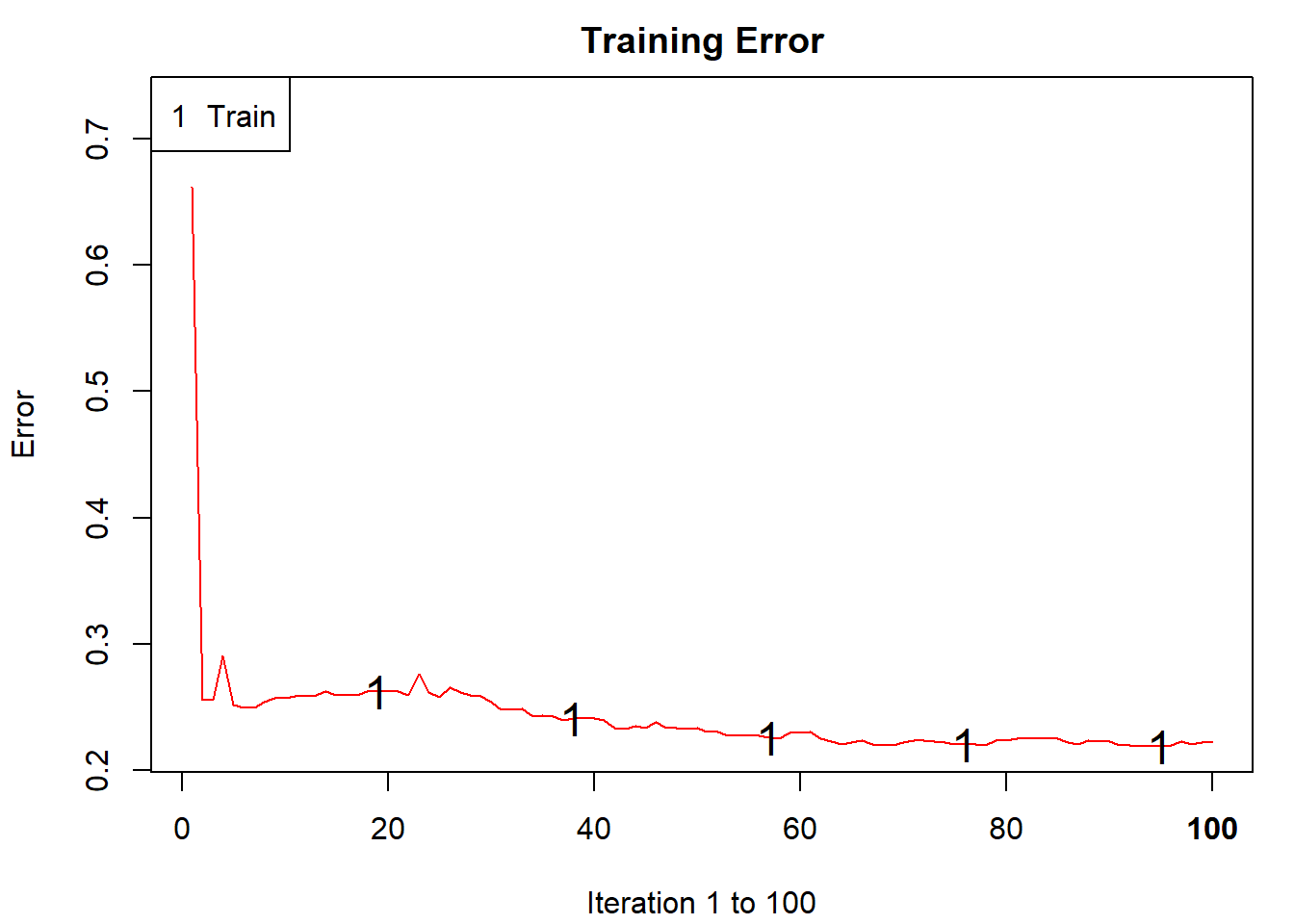
Evolución de la tasa de error utilizando ada().

Figura 4.11: Evolución de la tasa de error utilizando ada().

Podemos evaluar la precisión en la muestra de test empleando el procedimiento habitual:

pred <- predict(ada.boost, newdata = test)
caret::confusionMatrix(pred, test$taste, positive = "good")
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction bad good
##       bad   34   16
##       good  50  150
##                                        
##                Accuracy : 0.736        
##                  95% CI : (0.677, 0.79)
##     No Information Rate : 0.664        
##     P-Value [Acc > NIR] : 0.00861      
##                                        
##                   Kappa : 0.343        
##                                        
##  Mcnemar's Test P-Value : 4.87e-05     
##                                        
##             Sensitivity : 0.904        
##             Specificity : 0.405        
##          Pos Pred Value : 0.750        
##          Neg Pred Value : 0.680        
##              Prevalence : 0.664        
##          Detection Rate : 0.600        
##    Detection Prevalence : 0.800        
##       Balanced Accuracy : 0.654        
##                                        
##        'Positive' Class : good         
##

Para obtener las estimaciones de las probabilidades, habría que establecer type = "probs" al predecir (devolverá una matriz en la que cada columna se corresponde con un nivel):

p.est <- predict(ada.boost, newdata = test, type = "probs")
head(p.est)
##        [,1]    [,2]
## 1  0.498771 0.50123
## 4  0.309222 0.69078
## 9  0.027743 0.97226
## 10 0.045962 0.95404
## 12 0.442744 0.55726
## 16 0.373759 0.62624

Este procedimiento también está implementado en el paquete caret seleccionando el método "ada", que considera como hiperparámetros:

library(caret)
modelLookup("ada")
##   model parameter          label forReg forClass probModel
## 1   ada      iter         #Trees  FALSE     TRUE      TRUE
## 2   ada  maxdepth Max Tree Depth  FALSE     TRUE      TRUE
## 3   ada        nu  Learning Rate  FALSE     TRUE      TRUE

Por defecto la función train() solo considera nueve combinaciones de hiperparámetros (en lugar de las 27 que cabría esperar):

set.seed(1)
trControl <- trainControl(method = "cv", number = 5)
caret.ada0 <- train(taste ~ ., method = "ada", data = train, 
                    trControl = trControl)
caret.ada0
## Boosted Classification Trees 
## 
## 1000 samples
##   11 predictor
##    2 classes: 'bad', 'good' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 800, 801, 800, 800, 799 
## Resampling results across tuning parameters:
## 
##   maxdepth  iter  Accuracy  Kappa  
##   1          50   0.71001   0.24035
##   1         100   0.72203   0.28249
##   1         150   0.73603   0.33466
##   2          50   0.75298   0.38729
##   2         100   0.75397   0.40196
##   2         150   0.75597   0.41420
##   3          50   0.75700   0.41128
##   3         100   0.75503   0.41500
##   3         150   0.76500   0.44088
## 
## Tuning parameter 'nu' was held constant at a value of 0.1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were iter = 150, maxdepth = 3 and
##  nu = 0.1.

En la salida anterior, se observa que el parámetro nu se ha fijado en 0.1, por lo que solo se tienen los resultados para las combinaciones de maxdepth e iter. Se puede aumentar el número de combinaciones empleando tuneLength o tuneGrid, pero la búsqueda en una rejilla completa puede incrementar considerablemente el tiempo de computación. Por este motivo, se suelen seguir procedimientos alternativos de búsqueda. Por ejemplo, fijar la tasa de aprendizaje (inicialmente a un valor alto) para seleccionar primero un número de interaciones y la complejidad del árbol, y posteriormente fijar estos valores para seleccionar una nueva tasa de aprendizaje (repitiendo el proceso, si es necesario, hasta conseguir convergencia).

set.seed(1)
tuneGrid <- data.frame(iter = 150, maxdepth = 3,
                       nu = c(0.3, 0.1, 0.05, 0.01, 0.005))
caret.ada1 <- train(taste ~ ., method = "ada", data = train,
                    tuneGrid = tuneGrid, trControl = trControl)
caret.ada1
## Boosted Classification Trees 
## 
## 1000 samples
##   11 predictor
##    2 classes: 'bad', 'good' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 800, 801, 800, 800, 799 
## Resampling results across tuning parameters:
## 
##   nu     Accuracy  Kappa  
##   0.005  0.74397   0.37234
##   0.010  0.74398   0.37260
##   0.050  0.75598   0.41168
##   0.100  0.76198   0.43652
##   0.300  0.75801   0.44051
## 
## Tuning parameter 'iter' was held constant at a value of 150
## 
## Tuning parameter 'maxdepth' was held constant at a value of 3
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were iter = 150, maxdepth = 3 and
##  nu = 0.1.

Por último, podemos evaluar la precisión del modelo en la muestra de test:

confusionMatrix(predict(caret.ada1, newdata = test), 
                test$taste, positive = "good")
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction bad good
##       bad   40   21
##       good  44  145
##                                         
##                Accuracy : 0.74          
##                  95% CI : (0.681, 0.793)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 0.00584       
##                                         
##                   Kappa : 0.375         
##                                         
##  Mcnemar's Test P-Value : 0.00636       
##                                         
##             Sensitivity : 0.873         
##             Specificity : 0.476         
##          Pos Pred Value : 0.767         
##          Neg Pred Value : 0.656         
##              Prevalence : 0.664         
##          Detection Rate : 0.580         
##    Detection Prevalence : 0.756         
##       Balanced Accuracy : 0.675         
##                                         
##        'Positive' Class : good          
##

Ejercicio 4.3 Continuando con el Ejercicio 4.2 y utilizando la misma partición, vuelve a clasificar los individuos según su nivel de grasa corporal (bfan), pero ahora empleando boosting mediante el método "ada" del paquete caret:

  1. Selecciona los valores “óptimos” de los hiperparámetros considerando las posibles combinaciones de iter = c(75, 150), maxdepth = 1:2 y nu = c(0.5, 0.25, 0.1), mediante validación cruzada con 5 grupos. Representa la precisión de CV dependiendo de los valores de los hiperparámetros.

  2. Representa la evolución del error de clasificación al aumentar el número de iteraciones del algoritmo.

  3. Estudia la importancia de los predictores y el efecto del más importante.

  4. Evalúa la precisión de las predicciones en la muestra de test y compara los resultados con los obtenidos en el Ejercicio 4.2.

4.5.2 Ejemplo: regresión con el paquete gbm

El paquete gbm (B. Greenwell et al., 2022) implementa el algoritmo SGB de Friedman (2002) y admite varios tipos de respuesta considerando distintas funciones de pérdida (aunque en el caso de variables dicotómicas estas deben45 tomar valores en \(\{0, 1\}\)). La función principal es gbm() y se suelen considerar los siguientes argumentos:

gbm( formula, distribution = "bernoulli", data, n.trees = 100, 
     interaction.depth = 1, n.minobsinnode = 10, shrinkage = 0.1, 
     bag.fraction = 0.5, cv.folds = 0, n.cores = NULL)

  • formula y data (opcional): permiten especificar la respuesta y las variables predictoras de la forma habitual (típicamente respuesta ~ .; también está disponible una interfaz con matrices gbm.fit()).

  • distribution (opcional): texto con el nombre de la distribución (o lista con el nombre en name y parámetros adicionales en los demás componentes) que determina la función de pérdida. Si se omite, se establecerá a partir del tipo de la respuesta: "bernouilli" (regresión logística) si es una variable dicotómica 0/1, "multinomial" (regresión multinomial) si es un factor (no se recomienda) y "gaussian" (error cuadrático) en caso contrario. Otras opciones que pueden ser de interés son: "laplace" (error absoluto), "adaboost" (pérdida exponencial para respuestas dicotómicas 0/1), "huberized" (pérdida de Huber para respuestas dicotómicas 0/1), "poisson" (regresión de Poisson) y "quantile" (regresión cuantil).

  • ntrees: iteraciones/número de árboles que se crecerán; por defecto 100 (se puede emplear la función gbm.perf() para seleccionar un valor “óptimo”).

  • interaction.depth: profundidad de los árboles; por defecto 1 (modelo aditivo).

  • n.minobsinnode: número mínimo de observaciones en un nodo terminal; por defecto 10.

  • shrinkage: parámetro de regularización \(\lambda\); por defecto 0.1.

  • bag.fraction: proporción de observaciones seleccionadas al azar para crecer cada árbol; por defecto 0.5.

  • cv.folds: número de grupos para validación cruzada; por defecto 0 (no se hace validación cruzada). Si se asigna un valor mayor que 1, se realizará validación cruzada y se devolverá el error en la componente $cv.error (se puede emplear para seleccionar hiperparámetros).

  • n.cores: número de núcleos para el procesamiento en paralelo.

Como ejemplo emplearemos el conjunto de datos winequality, considerando la variable quality como respuesta:

data(winequality, package = "mpae")
set.seed(1)
df <- winequality
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

Ajustamos el modelo SGB:

library(gbm)
gbm.fit <- gbm(quality ~ ., data = train) #  distribution = "gaussian"
## Distribution not specified, assuming gaussian ...
gbm.fit
## gbm(formula = quality ~ ., data = train)
## A gradient boosted model with gaussian loss function.
## 100 iterations were performed.
## There were 11 predictors of which 11 had non-zero influence.

El método summary() calcula las medidas de influencia de los predictores y las representa gráficamente (ver Figura 4.12):

summary(gbm.fit)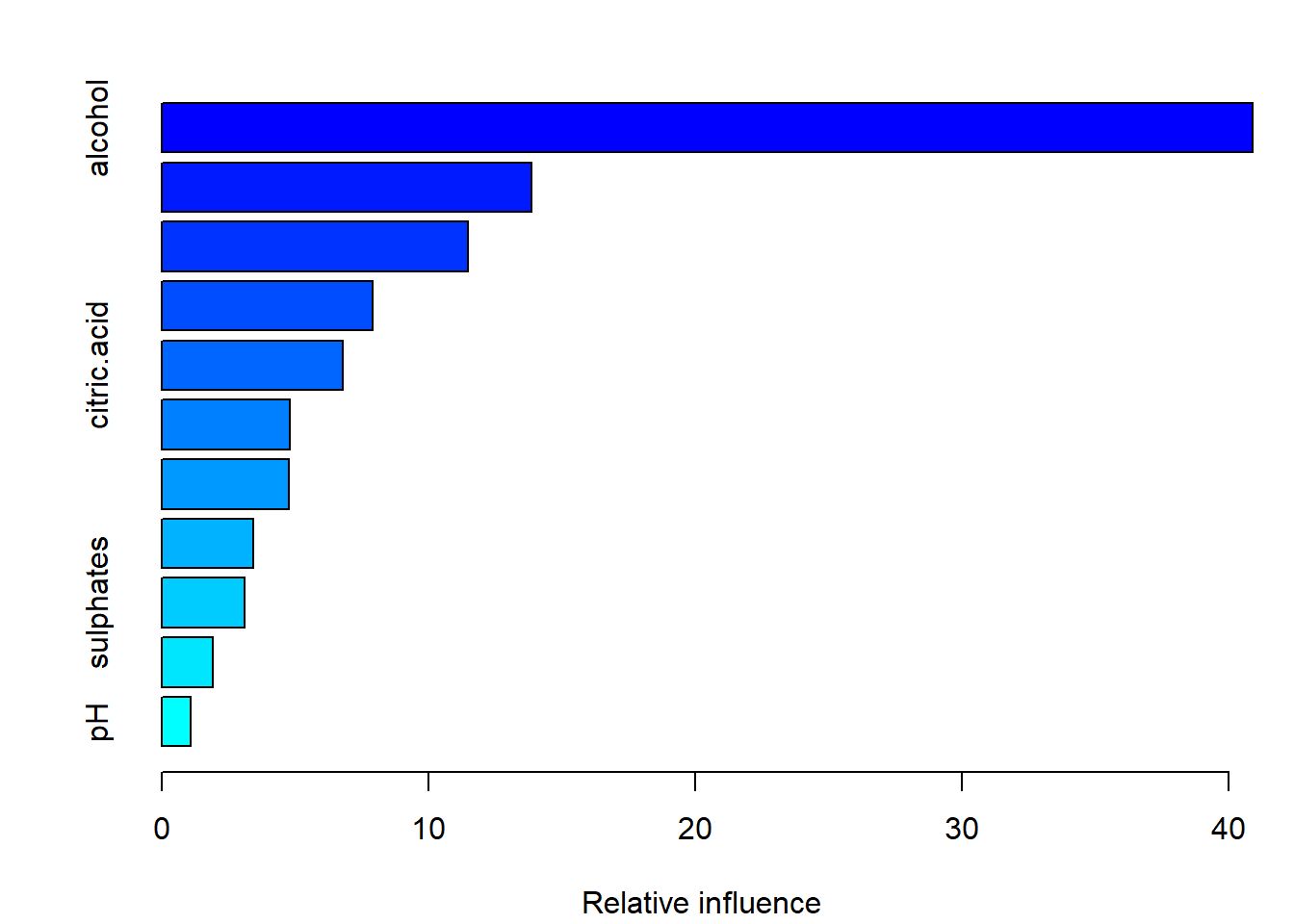
Importancia de las variables predictoras (con los valores por defecto de gbm()).

Figura 4.12: Importancia de las variables predictoras (con los valores por defecto de gbm()). 

##                                       var rel.inf
## alcohol                           alcohol 40.9080
## volatile.acidity         volatile.acidity 13.8391
## free.sulfur.dioxide   free.sulfur.dioxide 11.4883
## fixed.acidity               fixed.acidity  7.9147
## citric.acid                   citric.acid  6.7659
## total.sulfur.dioxide total.sulfur.dioxide  4.8083
## residual.sugar             residual.sugar  4.7586
## chlorides                       chlorides  3.4245
## sulphates                       sulphates  3.0860
## density                           density  1.9184
## pH                                     pH  1.0882

Para estudiar el efecto de un predictor se pueden generar gráficos de los efectos parciales mediante el método plot(), que llama internamente a las herramientas del paquete pdp. Por ejemplo, en la Figura 4.13 se representan los efectos parciales de los dos predictores más importantes:

p1 <- plot(gbm.fit, i = "alcohol")
p2 <- plot(gbm.fit, i = "volatile.acidity")
gridExtra::grid.arrange(p1, p2, ncol = 2)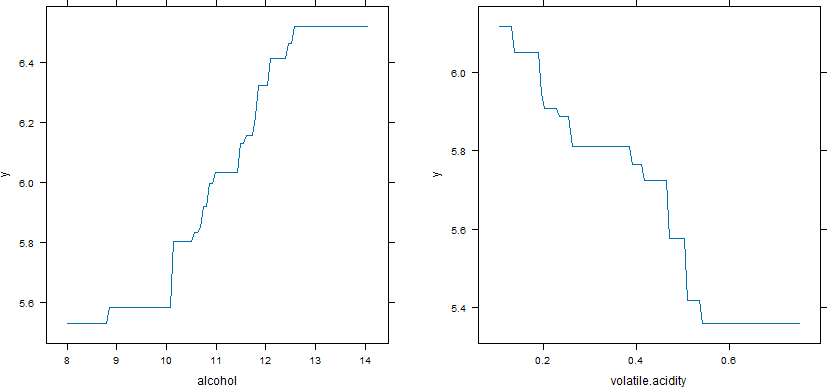
Efecto parcial del alcohol (panel izquierdo) y la acidez volátil (panel derecho) sobre la respuesta, en el modelo SGB ajustado.

Figura 4.13: Efecto parcial del alcohol (panel izquierdo) y la acidez volátil (panel derecho) sobre la respuesta, en el modelo SGB ajustado.

Finalmente, podemos evaluar la precisión en la muestra de test empleando el código habitual:

pred <- predict(gbm.fit, newdata = test)
obs <- test$quality
accuracy(pred, obs)
##        me      rmse       mae       mpe      mape r.squared 
## -0.014637  0.758621  0.611044 -2.007021 10.697537  0.299176

Este procedimiento también está implementado en el paquete caret seleccionando el método "gbm", que considera 4 hiperparámetros:

library(caret)
modelLookup("gbm")
##   model         parameter                   label forReg forClass
## 1   gbm           n.trees   # Boosting Iterations   TRUE     TRUE
## 2   gbm interaction.depth          Max Tree Depth   TRUE     TRUE
## 3   gbm         shrinkage               Shrinkage   TRUE     TRUE
## 4   gbm    n.minobsinnode Min. Terminal Node Size   TRUE     TRUE
##   probModel
## 1      TRUE
## 2      TRUE
## 3      TRUE
## 4      TRUE

Aunque por defecto la función train() solo considera nueve combinaciones de hiperparámetros. Para hacer una búsqueda más completa se podría seguir un procedimiento análogo al empleado con el método anterior. Primero, seleccionamos los hiperparámetros interaction.depth y n.trees (con las opciones por defecto, manteniendo shrinkage y n.minobsinnode fijos, aunque sin imprimir el progreso durante la búsqueda):

set.seed(1)
trControl <- trainControl(method = "cv", number = 5)
caret.gbm0 <- train(quality ~ ., method = "gbm", data = train,
                   trControl = trControl, verbose = FALSE)
caret.gbm0
## Stochastic Gradient Boosting 
## 
## 1000 samples
##   11 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 800, 801, 800, 800, 799 
## Resampling results across tuning parameters:
## 
##   interaction.depth  n.trees  RMSE     Rsquared  MAE    
##   1                   50      0.74641  0.29178   0.59497
##   1                  100      0.72583  0.31710   0.57518
##   1                  150      0.72472  0.31972   0.57194
##   2                   50      0.71982  0.33077   0.57125
##   2                  100      0.71750  0.33329   0.56474
##   2                  150      0.72582  0.32220   0.57131
##   3                   50      0.72417  0.31964   0.57226
##   3                  100      0.72721  0.31913   0.57544
##   3                  150      0.73114  0.31529   0.57850
## 
## Tuning parameter 'shrinkage' was held constant at a value of 0.1
## 
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were n.trees =
##  100, interaction.depth = 2, shrinkage = 0.1 and n.minobsinnode = 10.

A continuación elegimos shrinkage, fijando la selección previa de interaction.depth y n.trees (también se podría incluir n.minobsinnode en la búsqueda, pero lo mantenemos fijo para reducir el tiempo de computación):

tuneGrid <- data.frame(n.trees =  100, interaction.depth = 2, 
              n.minobsinnode = 10, shrinkage = c(0.3, 0.1, 0.05, 0.01, 0.005))
caret.gbm1 <- train(quality ~ ., method = "gbm", data = train,
                  tuneGrid = tuneGrid, trControl = trControl, verbose = FALSE)
caret.gbm1
## Stochastic Gradient Boosting 
## 
## 1000 samples
##   11 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 800, 800, 801, 799, 800 
## Resampling results across tuning parameters:
## 
##   shrinkage  RMSE     Rsquared  MAE    
##   0.005      0.81549  0.24191   0.62458
##   0.010      0.78443  0.26030   0.61286
##   0.050      0.72070  0.32755   0.57073
##   0.100      0.71248  0.34076   0.56317
##   0.300      0.77208  0.26138   0.60918
## 
## Tuning parameter 'n.trees' was held constant at a value of 100
## 
## Tuning parameter 'interaction.depth' was held constant at a value of
##  2
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were n.trees =
##  100, interaction.depth = 2, shrinkage = 0.1 and n.minobsinnode = 10.

Por último, evaluamos el modelo resultante en la muestra de test:

pred <- predict(caret.gbm1, newdata = test)
accuracy(pred, obs)
##        me      rmse       mae       mpe      mape r.squared 
## -0.020136  0.740377  0.601728 -1.984661 10.530266  0.332479

Ejercicio 4.4 Repite los pasos del ejemplo anterior (empleando el método gbm del paquete caret, seleccionando primero los hiperparámetros interaction.depth y n.trees con las opciones por defecto, y posteriormente shrinkage fijando la selección previa de los otros parámetros), empleando el conjunto de datos bodyfat del paquete mpae y considerando como respuesta la variable bodyfat (porcentaje de grasa corporal).

4.5.3 Ejemplo: XGBoost con el paquete caret

El método boosting implementado en el paquete xgboost (Chen et al., 2023) es uno de los más populares hoy en día. Esta implementación proporciona parámetros adicionales de regularización para controlar la complejidad del modelo y tratar de evitar el sobreajuste. También incluye criterios de parada para detener la evaluación del modelo cuando los árboles adicionales no ofrecen ninguna mejora. El paquete dispone de una interfaz simple, xgboost(), y otra más avanzada, xgb.train(), que admite funciones de pérdida y evaluación personalizadas. Normalmente es necesario un preprocesado de los datos antes de llamar a estas funciones, ya que requieren de una matriz para los predictores y de un vector para la respuesta; además, en el caso de que la respuesta sea dicotómica debe tomar valores en \(\{0, 1\}\)). Por tanto, es necesario recodificar las variables categóricas como numéricas. Por este motivo, puede ser preferible emplear la interfaz de caret.

El algoritmo estándar XGBoost, que emplea árboles como modelo base, está implementado en el método "xgbTree" de caret46:

library(caret)
# names(getModelInfo("xgb"))
modelLookup("xgbTree")
##     model        parameter                          label forReg
## 1 xgbTree          nrounds          # Boosting Iterations   TRUE
## 2 xgbTree        max_depth                 Max Tree Depth   TRUE
## 3 xgbTree              eta                      Shrinkage   TRUE
## 4 xgbTree            gamma         Minimum Loss Reduction   TRUE
## 5 xgbTree colsample_bytree     Subsample Ratio of Columns   TRUE
## 6 xgbTree min_child_weight Minimum Sum of Instance Weight   TRUE
## 7 xgbTree        subsample           Subsample Percentage   TRUE
##   forClass probModel
## 1     TRUE      TRUE
## 2     TRUE      TRUE
## 3     TRUE      TRUE
## 4     TRUE      TRUE
## 5     TRUE      TRUE
## 6     TRUE      TRUE
## 7     TRUE      TRUE

Este método considera los siguientes hiperparámetros:

  • "nrounds": número de iteraciones boosting.

  • "max_depth": profundidad máxima del árbol; por defecto 6.

  • "eta": parámetro de regularización \(\lambda\); por defecto 0.3.

  • "gamma": mínima reducción de la pérdida para hacer una partición adicional en un nodo del árbol; por defecto 0.

  • "colsample_bytree": proporción de predictores seleccionados al azar para crecer cada árbol; por defecto 1.

  • "min_child_weight": suma mínima de peso (hessiana) para hacer una partición adicional en un nodo del árbol; por defecto 1.

  • "subsample": proporción de observaciones seleccionadas al azar en cada iteración boosting; por defecto 1.

Para más información sobre parámetros adicionales, se puede consultar la ayuda de xgboost::xgboost() o la lista detallada disponible en la Sección XGBoost Parameters del manual de XGBoost.

A modo de ejemplo, consideraremos un problema de clasificación empleando de nuevo el conjunto de datos de calidad de vino:

# data(winetaste, package = "mpae")
set.seed(1)
df <- winetaste
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

En este caso, la función train() considera por defecto 108 combinaciones de hiperparámetros y el tiempo de computación puede ser excesivo47 (en este caso sería recomendable emplear computación en paralelo, ver por ejemplo el Capítulo 9 del manual de caret, e incluso con búsqueda aleatoria en lugar de evaluar en una rejilla completa, incluyendo search = "random" en trainControl()48):

caret.xgb <- train(taste ~ ., method = "xgbTree", data = train,
                   trControl = trControl, verbosity = 0)
caret.xgb
## eXtreme Gradient Boosting 
## 
## 1000 samples
##   11 predictor
##    2 classes: 'bad', 'good' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 799, 801, 801, 799, 800 
## Resampling results across tuning parameters:
## 
##   eta  max_depth  colsample_bytree  subsample  nrounds  Accuracy
##   0.3  1          0.6               0.50        50      0.74795 
##   0.3  1          0.6               0.50       100      0.75096 
##   0.3  1          0.6               0.50       150      0.74802 
##   0.3  1          0.6               0.75        50      0.73895 
##   0.3  1          0.6               0.75       100      0.74996 
##   0.3  1          0.6               0.75       150      0.75199 
##   0.3  1          0.6               1.00        50      0.74794 
##   0.3  1          0.6               1.00       100      0.74395 
##   Kappa  
##   0.39977
##   0.42264
##   0.41424
##   0.37757
##   0.41789
##   0.41944
##   0.39332
##   0.39468
##  [ reached getOption("max.print") -- omitted 100 rows ]
## 
## Tuning parameter 'gamma' was held constant at a value of 0
## 
## Tuning parameter 'min_child_weight' was held constant at a value of 1
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were nrounds = 100, max_depth =
##  2, eta = 0.4, gamma = 0, colsample_bytree = 0.8, min_child_weight =
##  1 and subsample = 1.

Al imprimir el resultado del ajuste, observamos que fija los valores de los hiperparámetros gamma y min_child_weight. Adicionalmente, se podría seguir una estrategia de selección de los hiperparámetros similar a la empleada en los métodos anteriores, alternando la búsqueda de los valores óptimos de distintos grupos de hiperparámetros.

caret.xgb$bestTune
##    nrounds max_depth eta gamma colsample_bytree min_child_weight subsample
## 89     100         2 0.4     0              0.8                1         1

En este caso, en un siguiente paso, podríamos seleccionar gamma y min_child_weight manteniendo fijos nrounds = 100, max_depth = 2, eta = 0.4, colsample_bytree = 0.8 y subsample = 1.

Al finalizar, evaluaríamos el modelo resultante en la muestra de test:

confusionMatrix(predict(caret.xgb, newdata = test), test$taste)
## Confusion Matrix and Statistics
## 
##           Reference
## Prediction bad good
##       bad   38   19
##       good  46  147
##                                         
##                Accuracy : 0.74          
##                  95% CI : (0.681, 0.793)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 0.00584       
##                                         
##                   Kappa : 0.367         
##                                         
##  Mcnemar's Test P-Value : 0.00126       
##                                         
##             Sensitivity : 0.452         
##             Specificity : 0.886         
##          Pos Pred Value : 0.667         
##          Neg Pred Value : 0.762         
##              Prevalence : 0.336         
##          Detection Rate : 0.152         
##    Detection Prevalence : 0.228         
##       Balanced Accuracy : 0.669         
##                                         
##        'Positive' Class : bad           
##

Ejercicio 4.5 Considera el ajuste anterior caret.xgb como un paso inicial en la selección de hiperparámetros y busca valores óptimos para todos ellos de forma iterativa hasta convergencia.

Bibliografía

Chen, T., He, T., Benesty, M., Khotilovich, V., Tang, Y., Cho, H., Chen, K., Mitchell, R., Cano, I., Zhou, T., et al. (2023). xgboost: Extreme Gradient Boosting. https://cran.r-project.org/package=xgboost
Culp, M., Johnson, K., y Michailidis, G. (2006). ada: An R Package for Stochastic Boosting. Journal of Statistical Software, 17(2), 1-27. https://doi.org/10.18637/jss.v017.i02
Friedman, J. (2002). Stochastic gradient boosting. Computational Statistics & data analysis, 38(4), 367-378. https://doi.org/10.1016/S0167-9473(01)00065-2
Friedman, J., Hastie, T., y Tibshirani, R. (2000). Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). The Annals of Statistics, 28(2), 337-407. https://doi.org/10.1214/aos/1016218223
Greenwell, B., Boehmke, B., Cunningham, J., y Developers, G. (2022). gbm: Generalized Boosted Regression Models. https://cran.r-project.org/package=gbm
Vinayak, R. K., y Gilad-Bachrach, R. (2015). Dart: Dropouts meet multiple additive regression trees. Artificial Intelligence and Statistics, 489-497.

  1. Se puede evitar este inconveniente empleando la interfaz de caret.↩︎

  2. Otras alternativas son: "xgbDART" que también emplean árboles como modelo base, pero incluye el método DART (Vinayak y Gilad-Bachrach, 2015) para evitar sobreajuste (básicamente descarta árboles al azar en la secuencia), y "xgbLinear" que emplea modelos lineales.↩︎

  3. Además, se establece verbosity = 0 para evitar (cientos de) mensajes de advertencia: WARNING: src/c_api/c_api.cc:935: "ntree_limit" is deprecated, use "iteration_range" instead.↩︎

  4. El parámetro tuneLength especificaría el número total de combinaciones de parámetros que se evaluarían.↩︎