2.3 Otros métodos de clasificación

En regresión logística, y en la mayoría de los métodos de clasificación (por ejemplo, en los que veremos en capítulos siguientes), un objetivo fundamental es estimar la probabilidad a posteriori \[P(Y = k \vert \mathbf{X}=\mathbf{x})\] de que una observación correspondiente a \(\mathbf{x}\) pertenezca a la categoría \(k\), sin preocuparse por la distribución de las variables predictoras. Estos métodos son conocidos en la terminología de machine learning como métodos discriminadores (discriminative methods, p. ej. Ng y Jordan, 2001) y en la estadística como modelos de diseño fijo.

En esta sección vamos a ver métodos que reciben el nombre genérico de métodos generadores (generative methods)³³. Se caracterizan porque calculan las probabilidades a posteriori utilizando la distribución conjunta de \((\mathbf{X}, Y)\) y el teorema de Bayes: \[P(Y = k \vert \mathbf{X}=\mathbf{x}) = \frac{P(Y = k) f_k(\mathbf{x})}{\sum_{l=1}^K P(Y = l) f_l(\mathbf{x})}\] donde \(f_k(\mathbf{x})\) es la función de densidad del vector aleatorio \(\mathbf{X}=(X_1, X_2, \ldots, X_p)\) para una observación perteneciente a la clase \(k\), es decir, es una forma abreviada de escribir \(f(\mathbf{X}=\mathbf{x} \vert Y = k)\). En la jerga bayesiana a esta función se la conoce como verosimilitud (es la función de verosimilitud sin más que considerar que la observación muestral \(\mathbf{x}\) es fija y la variable es \(k\)) y se resume la fórmula anterior como³⁴ \[posterior \propto prior \times verosimilitud\]

Una vez estimadas las probabilidades a priori \(P(Y = k)\) y las densidades (verosimilitudes) \(f_k(\mathbf{x})\), tenemos las probabilidades a posteriori. Para estimar las funciones de densidad se puede utilizar un método paramétrico o uno no paramétrico. En el primer caso, lo más habitual es modelizar la distribución del vector de variables predictoras como normales multivariantes.

A continuación vamos a ver, desde el punto de vista aplicado, tres casos particulares de este enfoque, siempre suponiendo normalidad (para más detalles ver, por ejemplo, el Capítulo 11 de Dalpiaz, 2020).

2.3.1 Análisis discriminante lineal

El análisis discriminante lineal (LDA) se inicia en Fisher (1936), pero es Welch (1939) quien lo enfoca utilizando el teorema de Bayes. Asumiendo que \(X \vert Y = k \sim N(\mu_k, \Sigma)\), es decir, que todas las categorías comparten la misma matriz \(\Sigma\), se obtienen las funciones discriminantes, lineales en \(\mathbf{x}\), \[\mathbf{x}^t \Sigma^{-1} \mu_k - \frac{1}{2} \mu_k^t \Sigma^{-1} \mu_k + \mbox{log}(P(Y = k))\]

La dificultad técnica del método LDA reside en el cálculo de \(\Sigma^{-1}\). Cuando hay más variables predictoras que datos, o cuando las variables predictoras están fuertemente correlacionadas, hay un problema. Una solución pasa por aplicar análisis de componentes principales (PCA) para reducir la dimensión y tener predictores incorrelados antes de utilizar LDA. Aunque la solución anterior se utiliza mucho, hay que tener en cuenta que la reducción de la dimensión se lleva a cabo sin tener en cuenta la información de las categorías, es decir, la estructura de los datos en categorías. Una alternativa consiste en utilizar partial least squares discriminant analysis (PLSDA, Berntsson y Wold, 1986). La idea consiste en realizar una regresión por mínimos cuadrados parciales (PLSR), que se tratará en la Sección 6.2, siendo las categorías la respuesta, con el objetivo de reducir la dimensión a la vez que se maximiza la correlación con las respuestas.

Una generalización de LDA es el mixture discriminant analysis (Hastie y Tibshirani, 1996), en el que, siempre con la misma matriz \(\Sigma\), se contempla la posibilidad de que dentro de cada categoría haya múltiples subcategorías que únicamente difieren en la media. Las distribuciones dentro de cada clase se agregan mediante una mixtura de las distribuciones multivariantes.

A continuación se muestra un ejemplo de análisis discriminante lineal empleando la función MASS::lda(), considerando el problema de clasificación empleado en la Sección 2.2 anterior, en el que la respuesta es bfan, con la misma partición y los mismos predictores (para comparar los resultados).

library(MASS)
ld <- lda(bfan ~ abdomen + weight, data = train)
ld

## Call:
## lda(bfan ~ abdomen + weight, data = train)
## 
## Prior probabilities of groups:
##      No     Yes 
## 0.72959 0.27041 
## 
## Group means:
##     abdomen weight
## No    88.25 77.150
## Yes  103.06 90.487
## 
## Coefficients of linear discriminants:
##               LD1
## abdomen  0.186094
## weight  -0.056329

En este caso, al haber solo dos categorías se construye una única función discriminante lineal. Podemos examinar la distribución de los valores que toma esta función en la muestra de entrenamiento mediante el método plot.lda() (ver Figura 2.14):

plot(ld)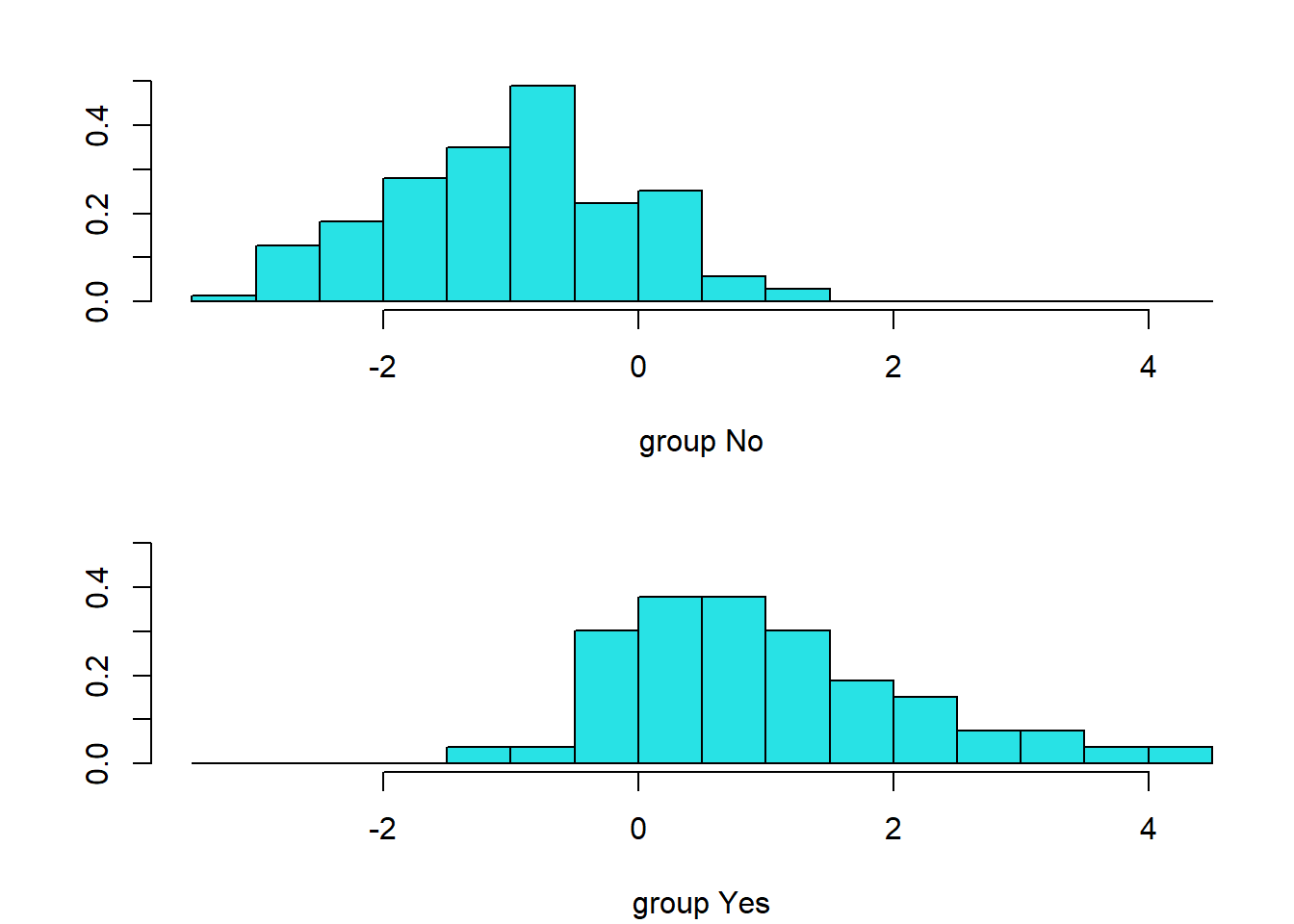

Figura 2.14: Distribución de los valores de la función discriminante lineal en cada clase.

Podemos evaluar la precisión en la muestra de test empleando la matriz de confusión:

pred <- predict(ld, newdata = test)
pred.ld <- pred$class
caret::confusionMatrix(pred.ld, test$bfan, positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction No Yes
##        No  27   6
##        Yes  2  15
##                                         
##                Accuracy : 0.84          
##                  95% CI : (0.709, 0.928)
##     No Information Rate : 0.58          
##     P-Value [Acc > NIR] : 7.98e-05      
##                                         
##                   Kappa : 0.663         
##                                         
##  Mcnemar's Test P-Value : 0.289         
##                                         
##             Sensitivity : 0.714         
##             Specificity : 0.931         
##          Pos Pred Value : 0.882         
##          Neg Pred Value : 0.818         
##              Prevalence : 0.420         
##          Detection Rate : 0.300         
##    Detection Prevalence : 0.340         
##       Balanced Accuracy : 0.823         
##                                         
##        'Positive' Class : Yes           
## 

También podríamos examinar las probabilidades estimadas:

p.est <- pred$posterior

2.3.2 Análisis discriminante cuadrático

El análisis discriminante cuadrático (QDA) relaja la suposición de que todas las categorías tengan la misma estructura de covarianzas, es decir, \(X \vert Y = k \sim N(\mu_k, \Sigma_k)\), obteniendo como solución \[-\frac{1}{2} (\mathbf{x} - \mu_k)^t \Sigma^{-1}_k (\mathbf{x} - \mu_k) - \frac{1}{2} \mbox{log}(|\Sigma_k|) + \mbox{log}(P(Y = k))\]

Vemos que este método da lugar a fronteras discriminantes cuadráticas.

Si el número de variables predictoras es próximo al tamaño muestral, en la práctica QDA se vuelve impracticable, ya que el número de variables predictoras tiene que ser menor que el número de datos en cada una de las categorías. Una recomendación básica es utilizar LDA y QDA únicamente cuando hay muchos más datos que predictores. Y al igual que en LDA, si dentro de las clases los predictores presentan mucha colinealidad el modelo va a funcionar mal.

Al ser QDA una generalización de LDA podemos pensar que siempre va a ser preferible, pero eso no es cierto, ya que QDA requiere estimar muchos más parámetros que LDA y por tanto tiene más riesgo de sobreajustar. Al ser menos flexible, LDA da lugar a modelos más simples: menos varianza pero más sesgo. LDA suele funcionar mejor que QDA cuando hay pocos datos y es por tanto muy importante reducir la varianza. Por el contrario, QDA es recomendable cuando hay muchos datos.

Una solución intermedia entre LDA y QDA es el análisis discriminante regularizado (RDA, Friedman, 1989), que utiliza el hiperparámetro \(\lambda\) para definir la matriz \[\Sigma_{k,\lambda}' = \lambda\Sigma_k + (1 - \lambda) \Sigma\]

También hay una versión con dos hiperparámetros, \(\lambda\) y \(\gamma\), \[\Sigma_{k,\lambda,\gamma}' = (1 - \gamma) \Sigma_{k,\lambda}' + \gamma \frac{1}{p} \mbox{tr} (\Sigma_{k,\lambda}')I\]

De modo análogo al caso lineal, podemos realizar un análisis discriminante cuadrático empleando la función MASS::qda():

qd <- qda(bfan ~ abdomen + weight, data = train)
qd

## Call:
## qda(bfan ~ abdomen + weight, data = train)
## 
## Prior probabilities of groups:
##      No     Yes 
## 0.72959 0.27041 
## 
## Group means:
##     abdomen weight
## No    88.25 77.150
## Yes  103.06 90.487

y evaluar la precisión en la muestra de test:

pred <- predict(qd, newdata = test)
pred.qd <- pred$class
# p.est <- pred$posterior
caret::confusionMatrix(pred.qd, test$bfan, positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction No Yes
##        No  27   6
##        Yes  2  15
##                                         
##                Accuracy : 0.84          
##                  95% CI : (0.709, 0.928)
##     No Information Rate : 0.58          
##     P-Value [Acc > NIR] : 7.98e-05      
##                                         
##                   Kappa : 0.663         
##                                         
##  Mcnemar's Test P-Value : 0.289         
##                                         
##             Sensitivity : 0.714         
##             Specificity : 0.931         
##          Pos Pred Value : 0.882         
##          Neg Pred Value : 0.818         
##              Prevalence : 0.420         
##          Detection Rate : 0.300         
##    Detection Prevalence : 0.340         
##       Balanced Accuracy : 0.823         
##                                         
##        'Positive' Class : Yes           
## 

En este caso vemos que se obtiene el mismo resultado que con el discriminante lineal del ejemplo anterior.

2.3.3 Bayes naíf

El método Bayes naíf (naive Bayes, Bayes ingenuo) es una simplificación de los métodos discriminantes anteriores en la que se asume que las variables explicativas son independientes. Esta es una suposición extremadamente fuerte y en la práctica difícilmente nos encontraremos con un problema en el que los predictores sean independientes, pero a cambio se va a reducir mucho la complejidad del modelo. Esta simplicidad del modelo le va a permitir manejar un gran número de predictores, incluso con un tamaño muestral moderado, en situaciones en las que puede ser imposible utilizar LDA o QDA. Otra ventaja asociada con su simplicidad es que el cálculo de las predicciones va a poder hacerse muy rápido incluso para tamaños muestrales muy grandes. Además, y quizás esto sea lo más sorprendente, en ocasiones su rendimiento es muy competitivo.

Asumiendo normalidad, este modelo no es más que un caso particular de QDA con matrices \(\Sigma_k\) diagonales. Cuando las variables predictoras son categóricas, lo más habitual es modelizar su distribución utilizando distribuciones multinomiales. Siguiendo con los ejemplos anteriores, empleamos la función e1071::naiveBayes() para realizar la clasificación:

library(e1071)
nb <- naiveBayes(bfan ~ abdomen + weight, data = train)
nb

## 
## Naive Bayes Classifier for Discrete Predictors
## 
## Call:
## naiveBayes.default(x = X, y = Y, laplace = laplace)
## 
## A-priori probabilities:
## Y
##      No     Yes 
## 0.72959 0.27041 
## 
## Conditional probabilities:
##      abdomen
## Y       [,1]   [,2]
##   No   88.25 7.4222
##   Yes 103.06 8.7806
## 
##      weight
## Y       [,1]   [,2]
##   No  77.150 10.527
##   Yes 90.487 11.144

En las tablas correspondientes a los predictores³⁵, se muestran la media y la desviación típica de sus distribuciones condicionadas a las distintas clases.

En este caso los resultados obtenidos en la muestra de test son peores:

pred.nb <- predict(nb, newdata = test)
# p.est <- predict(nb, newdata = test, type = "raw")
caret::confusionMatrix(pred.nb, test$bfan, positive = "Yes")

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction No Yes
##        No  25   7
##        Yes  4  14
##                                        
##                Accuracy : 0.78         
##                  95% CI : (0.64, 0.885)
##     No Information Rate : 0.58         
##     P-Value [Acc > NIR] : 0.00248      
##                                        
##                   Kappa : 0.539        
##                                        
##  Mcnemar's Test P-Value : 0.54649      
##                                        
##             Sensitivity : 0.667        
##             Specificity : 0.862        
##          Pos Pred Value : 0.778        
##          Neg Pred Value : 0.781        
##              Prevalence : 0.420        
##          Detection Rate : 0.280        
##    Detection Prevalence : 0.360        
##       Balanced Accuracy : 0.764        
##                                        
##        'Positive' Class : Yes          
## 

Para finalizar, utilizamos mpae::pred.plot() para comparar los resultados de los distintos métodos empleados en este capítulo (ver Figura 2.15). Los mejores (globalmente) se obtuvieron con el modelo de regresión logística de la Sección 2.2.

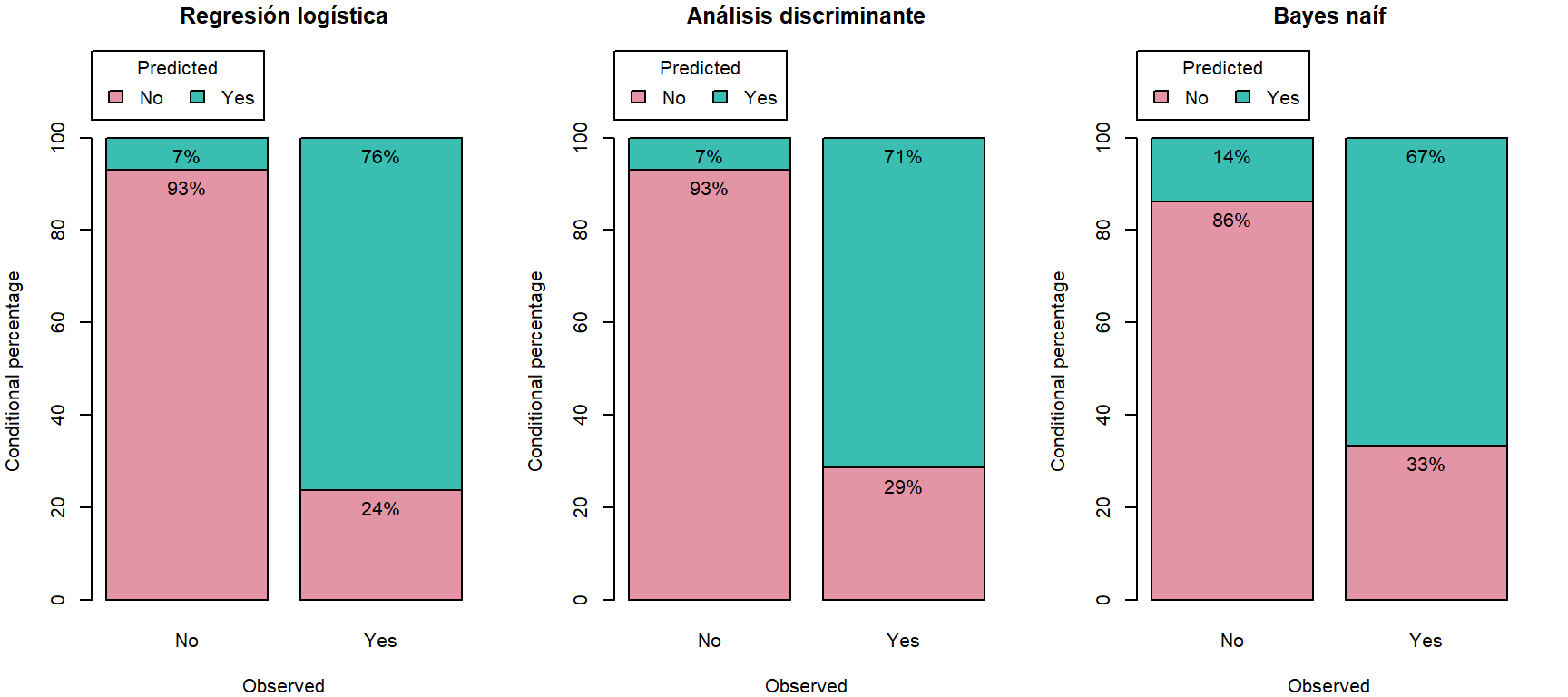
Figura 2.15: Resultados de la clasificación en la muestra de test obtenidos con los distintos métodos (distribuciones de las predicciones condicionadas a los valores observados).

Ejercicio 2.5 Continuando el Ejercicio 2.4, con los datos de calidad del vino winetaste, clasifica la calidad taste de los vinos mediante análisis discriminante lineal, análisis discriminante cuadrático y Bayes naíf. Compara los resultados de los distintos métodos, empleando la misma partición de los datos.

Bibliografía

Dalpiaz, D. (2020). R for Statistical Learning. https://daviddalpiaz.github.io/r4sl. https://daviddalpiaz.github.io/r4sl

Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of eugenics, 7(2), 179-188. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x

Friedman, J. (1989). Regularized discriminant analysis. Journal of the American Statistical Association, 84(405), 165-175. https://doi.org/10.1080/01621459.1989.10478752

Hastie, T., y Tibshirani, R. (1996). Discriminant Analysis by Gaussian Mixtures. Journal of the Royal Statistical Society. Series B (Methodological), 58(1), 155-176. https://doi.org/10.1111/j.2517-6161.1996.tb02073.x

Ng, A., y Jordan, M. (2001). On Discriminative vs. Generative Classifiers: A comparison of logistic regression and naive Bayes. En T. Dietterich, S. Becker, y Z. Ghahramani (Eds.), Advances in Neural Information Processing Systems. MIT Press. https://proceedings.neurips.cc/paper_files/paper/2001/file/7b7a53e239400a13bd6be6c91c4f6c4e-Paper.pdf

Welch, B. L. (1939). Note on Discriminant Functions. Biometrika, 31(1/2), 218-220. https://doi.org/10.2307/2334985

---

33. Ng y Jordan (2001) afirman, ya en la introducción del artículo, que: “Se debe resolver el problema (de clasificación) directamente y nunca resolver un problema más general como un paso intermedio (como modelar, también, \(P(\mathbf{X}=\mathbf{x} \vert Y = k)\)). De hecho, dejando a un lado detalles computacionales y cuestiones como la gestión de los datos faltantes, el consenso predominante parece ser que los clasificadores discriminadores son casi siempre preferibles a los generadores”.↩︎

34. Donde \(\propto\) indica “proporcional a”, igual salvo una constante multiplicadora; en este caso \(1/c\), donde \(c = f(\mathbf{X}=\mathbf{x})\) es la denominada constante normalizadora.↩︎

35. Aunque al imprimir los resultados aparece Naive Bayes Classifier for Discrete Predictors, se trata de un error. En este caso, todos los predictores son continuos.↩︎