2.1 Regresión lineal múltiple

En los modelos lineales se supone que la función de regresión es lineal²³: \[E( Y \vert \mathbf{X} ) = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p}\] siendo \(\left( \beta_{0},\beta_{1},\ldots,\beta_{p}\right)^t\) un vector de parámetros (desconocidos). Es decir, que el efecto de las variables explicativas sobre la respuesta es muy simple, proporcional a su valor, y por tanto la interpretación de este tipo de modelos es (en principio) muy fácil. El coeficiente \(\beta_j\) representa el incremento medio de \(Y\) al aumentar en una unidad el valor de \(X_j\), manteniendo fijas el resto de las covariables. En este contexto las variables predictoras se denominan habitualmente variables independientes, pero en la práctica es de esperar que no haya independencia entre ellas, por lo que puede no ser muy razonable pensar que al variar una de ellas el resto va a permanecer constante.

El ajuste de este tipo de modelos en la práctica se suele realizar empleando el método de mínimos cuadrados (ordinarios), asumiendo (implícita o explícitamente) que la distribución condicional de la respuesta es normal, lo que se conoce como el modelo de regresión lineal múltiple. Concretamente, el método tradicional considera el siguiente modelo: \[\begin{equation} Y = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\ldots+\beta_{p}X_{p} + \varepsilon, \tag{2.1} \end{equation}\] donde \(\varepsilon\) es un error aleatorio normal, de media cero y varianza \(\sigma^2\), independiente de las variables predictoras. Además, los errores de las distintas observaciones son independientes entre sí.

Por tanto las hipótesis estructurales del modelo son: linealidad (el efecto de los predictores es lineal), homocedasticidad (varianza constante del error), normalidad (y homogeneidad: ausencia de valores atípicos y/o influyentes) e independencia de los errores. Estas son también las hipótesis del modelo de regresión lineal simple (con una única variable explicativa); en regresión múltiple tendríamos la hipótesis adicional de que ninguna de las variables explicativas es combinación lineal de las demás. Esto está relacionado con el fenómeno de la colinealidad (o multicolinealidad), que se tratará en la Sección 2.1.1, y que es de especial interés en regresión múltiple (no solo en el caso lineal). Además, se da por hecho que el número de observaciones disponible es como mínimo el número de parámetros del modelo, \(n \geq p + 1\).

El procedimiento habitual para ajustar un modelo de regresión lineal a un conjunto de datos es emplear mínimos cuadrados (ordinarios; el método más eficiente bajo las hipótesis estructurales):

\[\mbox{min}_{\beta_{0},\beta_{1},\ldots,\beta_{p}} \sum\limits_{i=1}^{n}\left( y_{i} - \beta_0 - \beta_1 x_{1i} - \ldots - \beta_p x_{pi} \right)^{2} = \mbox{min}_{\beta_{0},\beta_{1},\ldots,\beta_{p}} \ RSS\]

denotando por RSS la suma de cuadrados residual (residual sum of squares), es decir, la suma de los residuos al cuadrado.

Para realizar este ajuste en R podemos emplear la función lm():

ajuste <- lm(formula, data, subset, weights, na.action, ...)

• formula: fórmula que especifica el modelo.

• data: data.frame (opcional) con las variables de la fórmula.

• subset: vector (opcional) que especifica un subconjunto de observaciones.

• weights: vector (opcional) de pesos (mínimos cuadrados ponderados, WLS).

• na.action: opción para manejar los datos faltantes; por defecto na.omit.

Alternativamente, se puede emplear la función biglm() del paquete biglm para ajustar modelos lineales a grandes conjuntos de datos (especialmente cuando el número de observaciones es muy grande, incluyendo el caso de que los datos excedan la capacidad de memoria del equipo). También se podría utilizar la función rlm() del paquete MASS para ajustar modelos lineales empleando un método robusto cuando hay datos atípicos.

Como ejemplo, consideraremos el conjunto de datos bodyfat del paquete mpae, que contiene observaciones de grasa corporal y mediciones corporales de una muestra de 246 hombres (Penrose et al., 1985).

library(mpae)
# data(bodyfat, package = "mpae")
as.data.frame(attr(bodyfat, "variable.labels"))

##                     attr(bodyfat, "variable.labels")
## bodyfat Percent body fat (from Siri's 1956 equation)
## age                                      Age (years)
## weight                                   Weight (kg)
## height                                   Height (cm)
## neck                         Neck circumference (cm)
## chest                       Chest circumference (cm)
## abdomen                   Abdomen circumference (cm)
## hip                           Hip circumference (cm)
## thigh                       Thigh circumference (cm)
## knee                         Knee circumference (cm)
## ankle                       Ankle circumference (cm)
## biceps          Biceps (extended) circumference (cm)
## forearm                   Forearm circumference (cm)
## wrist                       Wrist circumference (cm)

Consideraremos como respuesta la variable bodyfat, que mide la grasa corporal (en porcentaje) a partir de la densidad corporal, obtenida mediante un procedimiento costoso que requiere un pesaje subacuático. El objetivo es disponer de una forma más sencilla de estimar la grasa corporal a partir de medidas corporales. En este caso todos los predictores son numéricos; para una introducción al tratamiento de variables predictoras categóricas ver, por ejemplo, la Sección 8.5 de Fernández-Casal et al. (2022).

La regresión lineal es un método clásico de estadística y, por tanto, el procedimiento habitual es emplear toda la información disponible para construir el modelo y, posteriormente (asumiendo que es el verdadero), utilizar métodos de inferencia para evaluar su precisión. Sin embargo, seguiremos el procedimiento habitual en AE y particionaremos los datos en una muestra de entrenamiento y en otra de test.

df <- bodyfat 
set.seed(1)
nobs <- nrow(df)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
test <- df[-itrain, ]

El primer paso antes del modelado suele ser realizar un análisis descriptivo. Por ejemplo, podemos generar un gráfico de dispersión matricial y calcular la matriz de correlaciones (lineales de Pearson). Sin embargo, en muchos casos el número de variables es grande y en lugar de emplear gráficos de dispersión puede ser preferible representar gráficamente las correlaciones mediante un mapa de calor o algún gráfico similar. En la Figura 2.1 se combinan elipses con colores para representar las correlaciones.

# plot(train) # gráfico de dispersión matricial
mcor <- cor(train)
corrplot::corrplot(mcor, method = "ellipse")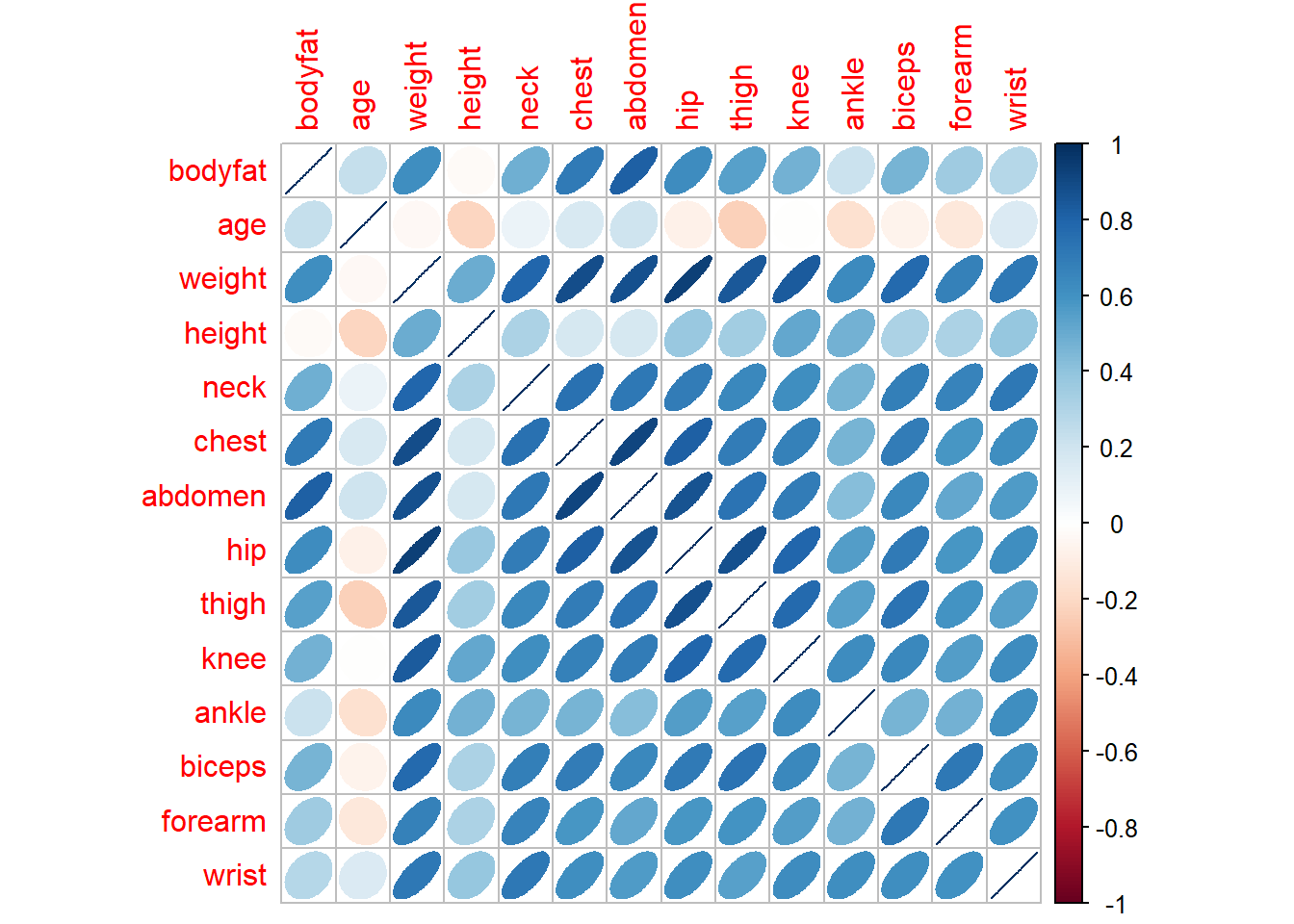

Figura 2.1: Representación de las correlaciones lineales entre las variables del conjunto de datos bodyfat, generada con la función corrplot::corrplot().

print(mcor, digits = 3)

##         bodyfat      age  weight  height   neck chest abdomen     hip
## bodyfat  1.0000  0.23003  0.6174 -0.0294 0.4820 0.701   0.816  0.6259
## age      0.2300  1.00000 -0.0384 -0.2145 0.0858 0.164   0.204 -0.0718
## weight   0.6174 -0.03838  1.0000  0.4923 0.7947 0.882   0.876  0.9313
## height  -0.0294 -0.21445  0.4923  1.0000 0.3116 0.179   0.177  0.3785
##          thigh     knee  ankle  biceps forearm wrist
## bodyfat  0.542  0.47448  0.213  0.4681   0.353 0.288
## age     -0.238 -0.00612 -0.167 -0.0662  -0.124 0.153
## weight   0.849  0.83207  0.630  0.7771   0.680 0.714
## height   0.342  0.51736  0.474  0.3101   0.312 0.390
##  [ reached getOption("max.print") -- omitted 10 rows ]

Observamos que, aparentemente, hay una relación (lineal) entre la respuesta bodyfat y algunas de las variables explicativas (que en principio no parece razonable suponer que sean independientes). Si consideramos un modelo de regresión lineal simple, el mejor ajuste se obtendría empleando abdomen como variable explicativa (ver Figura 2.2), ya que es la variable más correlacionada con la respuesta (la proporción de variabilidad explicada en la muestra de entrenamiento por este modelo, el coeficiente de determinación \(R^2\), sería \(0.816^2 \approx 0.666\)).

modelo <- lm(bodyfat ~ abdomen, data = train)
summary(modelo)

## 
## Call:
## lm(formula = bodyfat ~ abdomen, data = train)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -10.73  -3.49   0.25   3.08  13.02 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -41.8950     3.1071   -13.5   <2e-16 ***
## abdomen       0.6579     0.0335    19.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.77 on 194 degrees of freedom
## Multiple R-squared:  0.666,  Adjusted R-squared:  0.664 
## F-statistic:  386 on 1 and 194 DF,  p-value: <2e-16

plot(bodyfat ~ abdomen, data = train)
abline(modelo)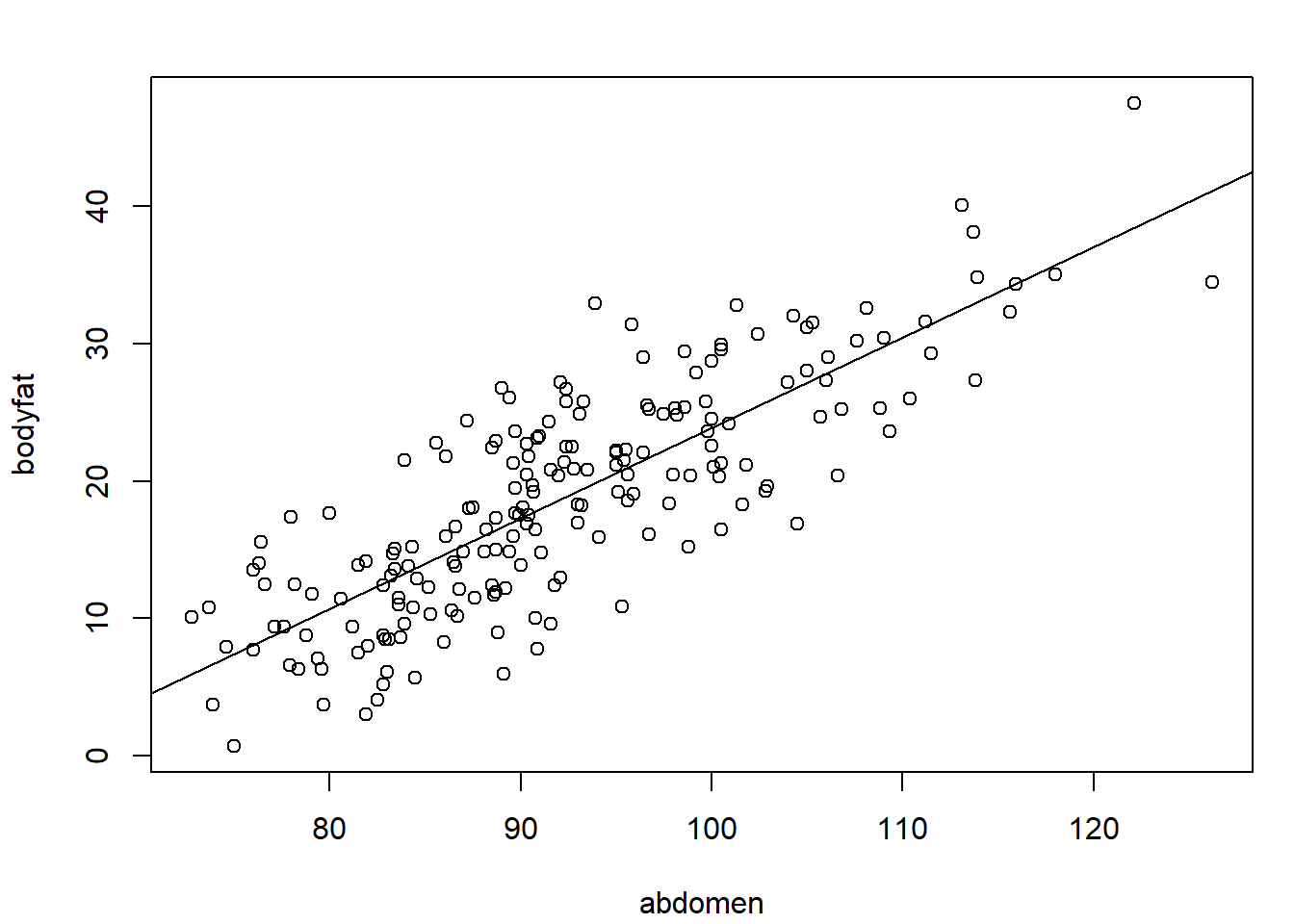

Figura 2.2: Gráfico de dispersión y recta de regresión ajustada para bodyfat en función de abdomen.

El método predict() permite calcular predicciones (estimaciones de la media condicional), intervalos de confianza para la media e intervalos de predicción para nuevas observaciones (la ayuda de predict.lm() proporciona todas las opciones disponibles). En la Figura 2.3 se muestra su representación gráfica.

# Predicciones
valores <- seq(70, 130, len = 100)
newdata <- data.frame(abdomen = valores)
pred <- predict(modelo, newdata = newdata, interval = "confidence")
# Representación
plot(bodyfat ~ abdomen, data = train)
matlines(valores, pred, lty = c(1, 2, 2), col = 1)
pred2 <- predict(modelo, newdata = newdata, interval = "prediction")
matlines(valores, pred2[, -1], lty = 3, col = 1)
leyenda <- c("Ajuste", "Int. confianza", "Int. predicción")
legend("topleft", legend = leyenda, lty = 1:3)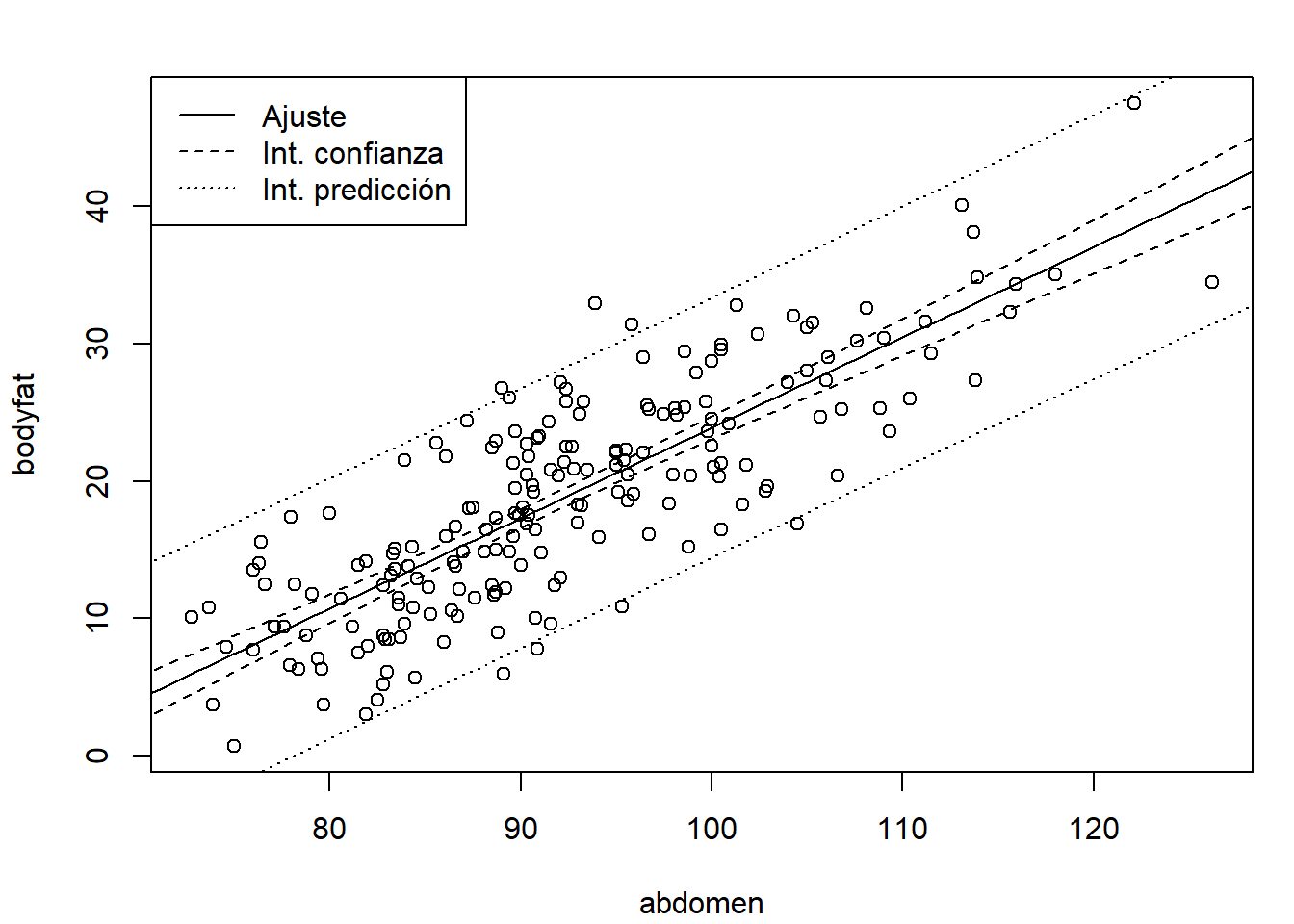

Figura 2.3: Ajuste lineal (predicciones) e intervalos de confianza y predicción (puntuales).

Para la extracción de información se puede acceder a las componentes del modelo ajustado o emplear funciones (genéricas; muchas de ellas válidas para otro tipo de modelos: rlm(), glm()…). Algunas de las más utilizadas se muestran en la Tabla 2.1.

Tabla 2.1: Listado de las principales funciones auxiliares para modelos ajustados.

Función	Descripción
fitted()	valores ajustados
coef()	coeficientes estimados (y errores estándar)
confint()	intervalos de confianza para los coeficientes
residuals()	residuos
plot()	gráficos de diagnóstico
termplot()	gráfico de efectos parciales
anova()	calcula tablas de análisis de varianza (también permite comparar modelos)
influence.measures()	calcula medidas de diagnóstico (“dejando uno fuera”; LOOCV)
update()	actualiza un modelo (por ejemplo, eliminando o añadiendo variables)

Ejercicio 2.1 Después de particionar los datos y ajustar el modelo inicial anterior:

modelo <- lm(bodyfat ~ abdomen, data = train)

ejecuta el siguiente código:

modelo2 <- update(modelo, . ~ . + wrist)
summary(modelo2)
confint(modelo2)
anova(modelo2)
anova(modelo, modelo2)
oldpar <- par(mfrow = c(1, 2))
termplot(modelo2, partial.resid = TRUE)
par(oldpar)

y responde a las siguientes preguntas sobre el ajuste obtenido al añadir wrist como predictor:

1. ¿Se produce una mejora en la proporción de variabilidad explicada?

2. ¿Esta mejora es significativa?

3. ¿Cuáles son las estimaciones de los coeficientes?

4. Compara el intervalo de confianza para el efecto de la variable abdomen (rango en el que confiaríamos que variase el porcentaje de grasa al aumentar un centímetro la circunferencia del abdomen) con el del modelo de regresión lineal simple anterior.

2.1.1 El problema de la colinealidad

Si alguna de las variables explicativas no aporta información relevante sobre la respuesta, puede aparecer el problema de la colinealidad. En regresión múltiple se supone que ninguna de las variables explicativas es combinación lineal de las demás. Si una de las variables explicativas (variables independientes) es combinación lineal de las otras, no se pueden determinar los parámetros de forma única. Sin llegar a esta situación extrema, cuando algunas variables explicativas estén altamente correlacionadas entre sí, tendremos una situación de alta colinealidad. En este caso, las estimaciones de los parámetros pueden verse seriamente afectadas:

• Tendrán varianzas muy altas (serán poco eficientes).

• Habrá mucha dependencia entre ellas (al modificar ligeramente el modelo, añadiendo o eliminando una variable o una observación, se producirán grandes cambios en las estimaciones de los efectos).

Consideraremos un ejemplo de regresión lineal bidimensional con datos simulados en el que las dos variables explicativas están altamente correlacionadas. Además, en este ejemplo solo una de las variables explicativas tiene un efecto lineal sobre la respuesta:

set.seed(1)
n <- 50
rand.gen <- runif
x1 <- rand.gen(n)
rho <- sqrt(0.99) # coeficiente de correlación
x2 <- rho*x1 + sqrt(1 - rho^2)*rand.gen(n)
fit.x2 <- lm(x2 ~ x1)
# plot(x1, x2); summary(fit.x2)
# Rejilla x-y para predicciones:
len.grid <- 30
x1.range <- range(x1)
x1.grid <- seq(x1.range[1], x1.range[2], len = len.grid)
x2.range <- range(x2)
x2.grid <- seq(x2.range[1], x2.range[2], len = len.grid)
xy <- expand.grid(x1 = x1.grid, x2 = x2.grid)
# Modelo teórico:
model.teor <- function(x1, x2) x1
# model.teor <- function(x1, x2) x1 - 0.5*x2
y.grid <- matrix(mapply(model.teor, xy$x1, xy$x2), nrow = len.grid)
y.mean <- mapply(model.teor, x1, x2)

Los valores de las variables explicativas y la tendencia teórica se muestran en la Figura 2.4:

library(plot3D)
ylim <- c(-2, 3) # range(y, y.pred)
scatter3D(z = y.mean, x = x1, y = x2, pch = 16, cex = 1, clim = ylim, 
          zlim = ylim, theta = -40, phi = 20, ticktype = "detailed", 
          xlab = "x1", ylab = "x2", zlab = "y", 
          surf = list(x = x1.grid, y = x2.grid, z = y.grid, facets = NA))
scatter3D(z = rep(ylim[1], n), x = x1, y = x2, add = TRUE, colkey = FALSE, 
           pch = 16, cex = 1, col = "black")
x2.pred <- predict(fit.x2, newdata = data.frame(x1 = x1.range))
lines3D(z = rep(ylim[1], 2), x = x1.range, y = x2.pred, add = TRUE, 
        colkey = FALSE, col = "black")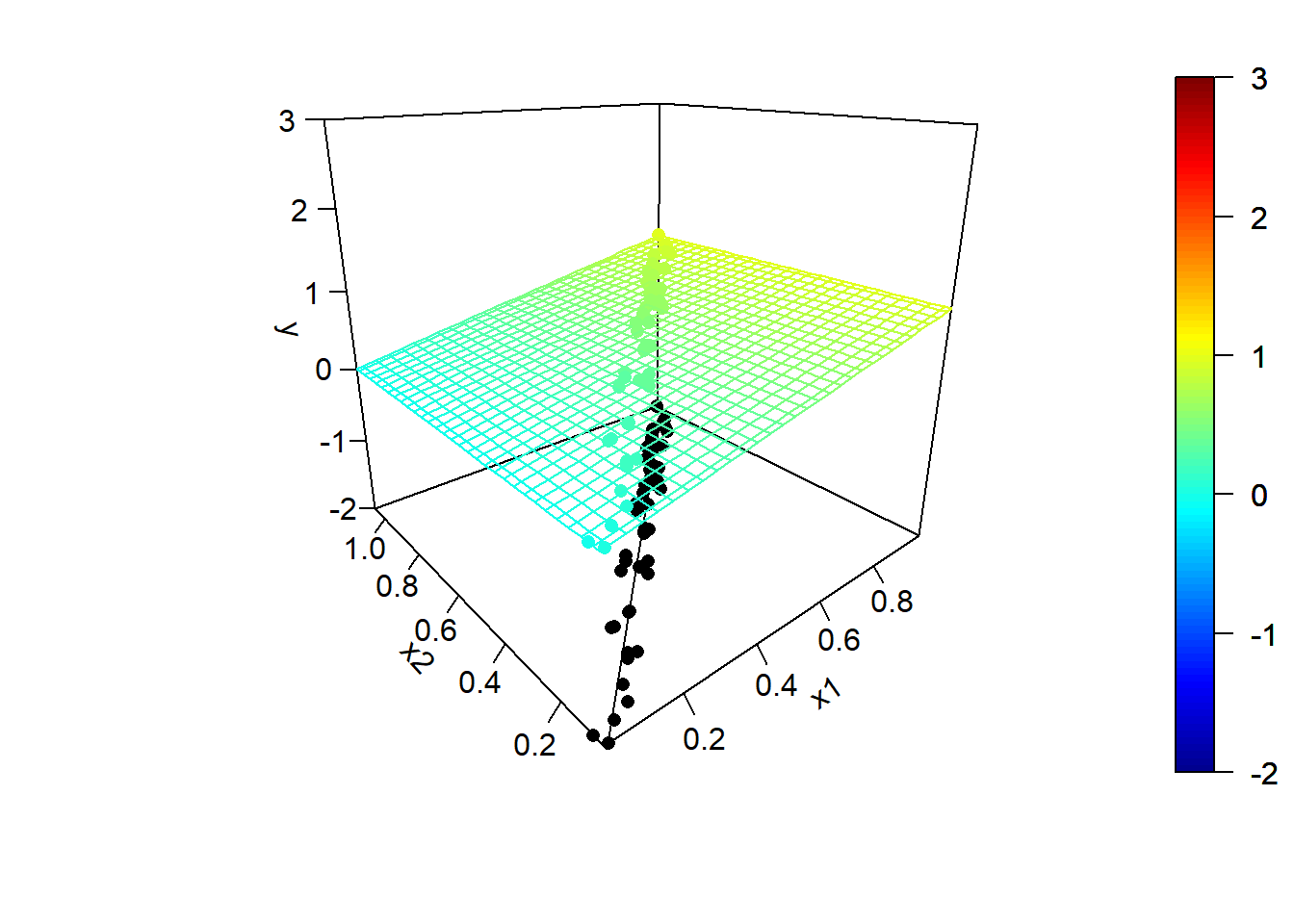 

Figura 2.4: Modelo teórico y valores de las variables explicativas (altamente correlacionadas, con un coeficiente de determinación de 0.99).

Para ilustrar el efecto de la correlación en los predictores, en la Figura 2.5 se muestran ejemplos de simulaciones bajo colinealidad y los correspondientes modelos ajustados. Los valores de la variable respuesta, los modelos ajustados y las superficies de predicción se han obtenido aplicando, reiteradamente:

y <- y.mean + rnorm(n, 0, 0.25)
fit <- lm(y ~ x1 + x2)
y.pred <- matrix(predict(fit, newdata = xy), nrow = length(x1.grid))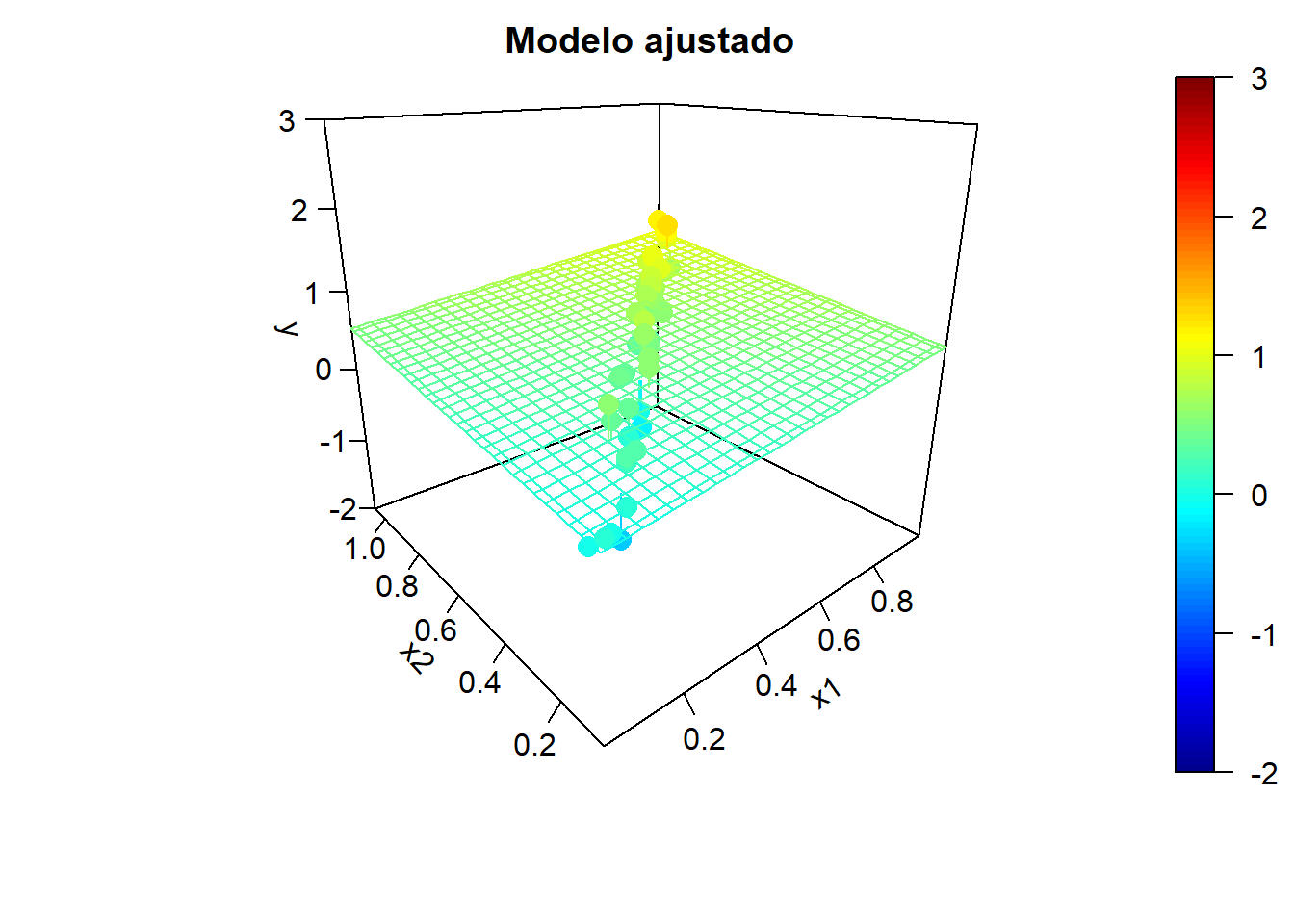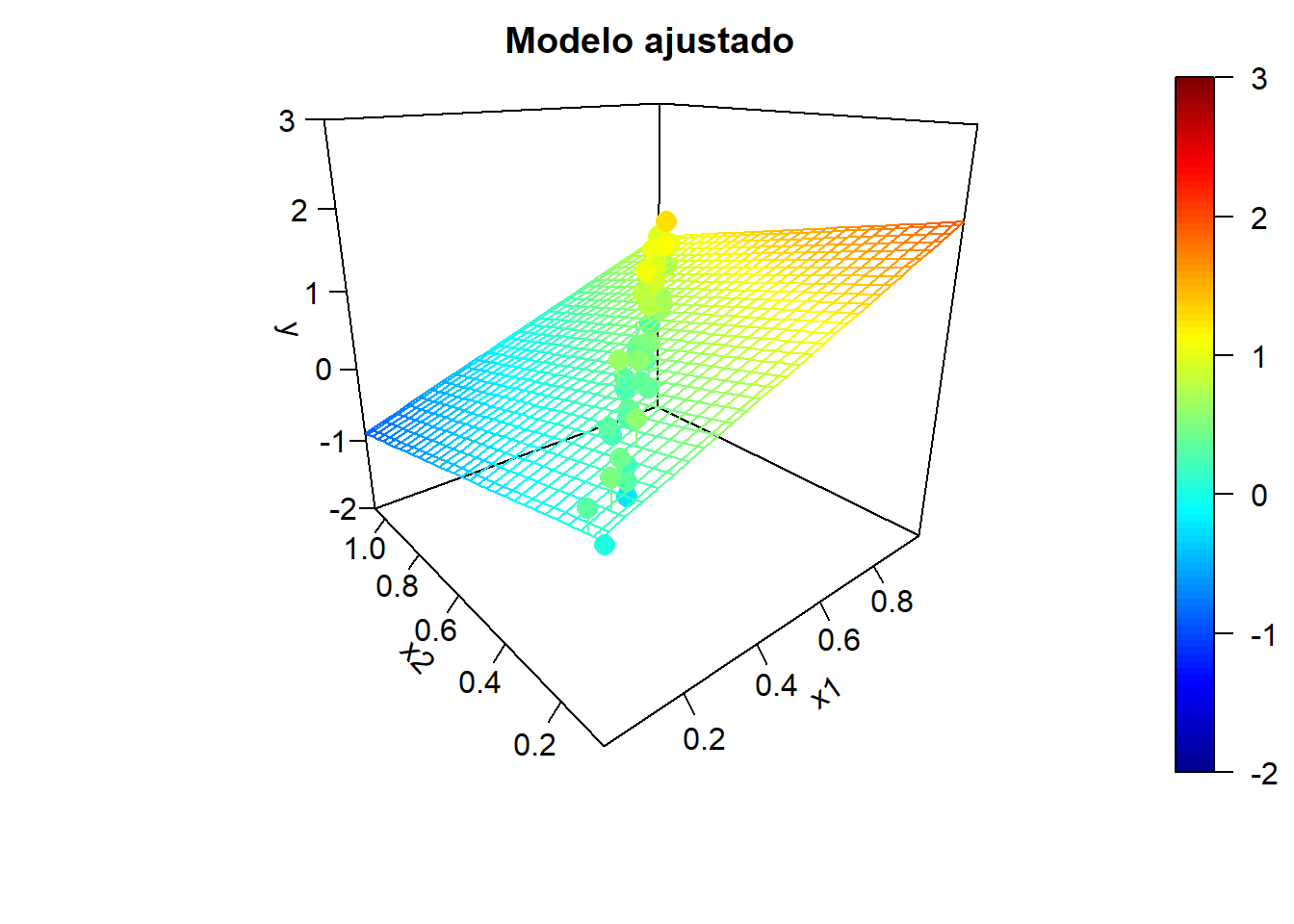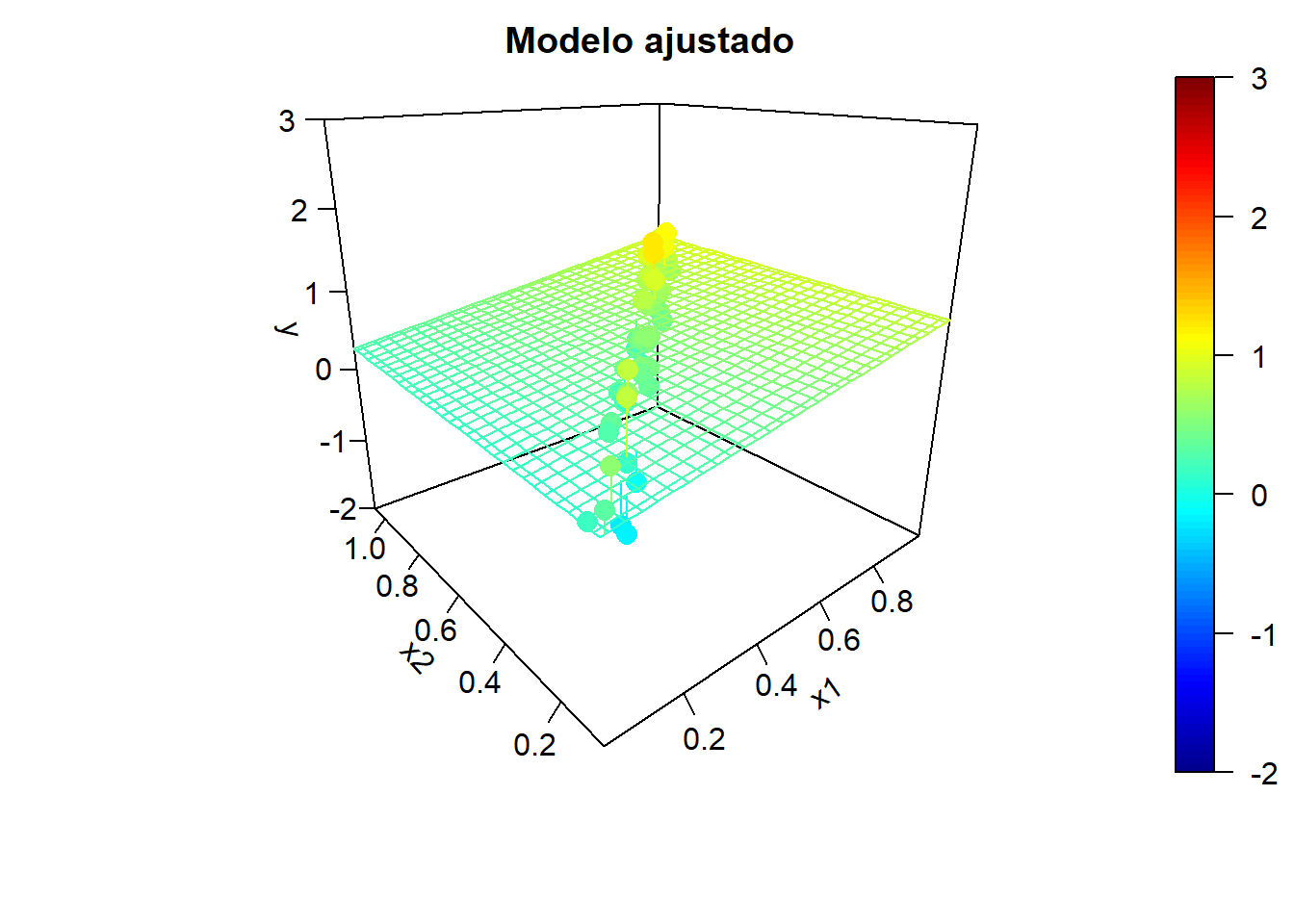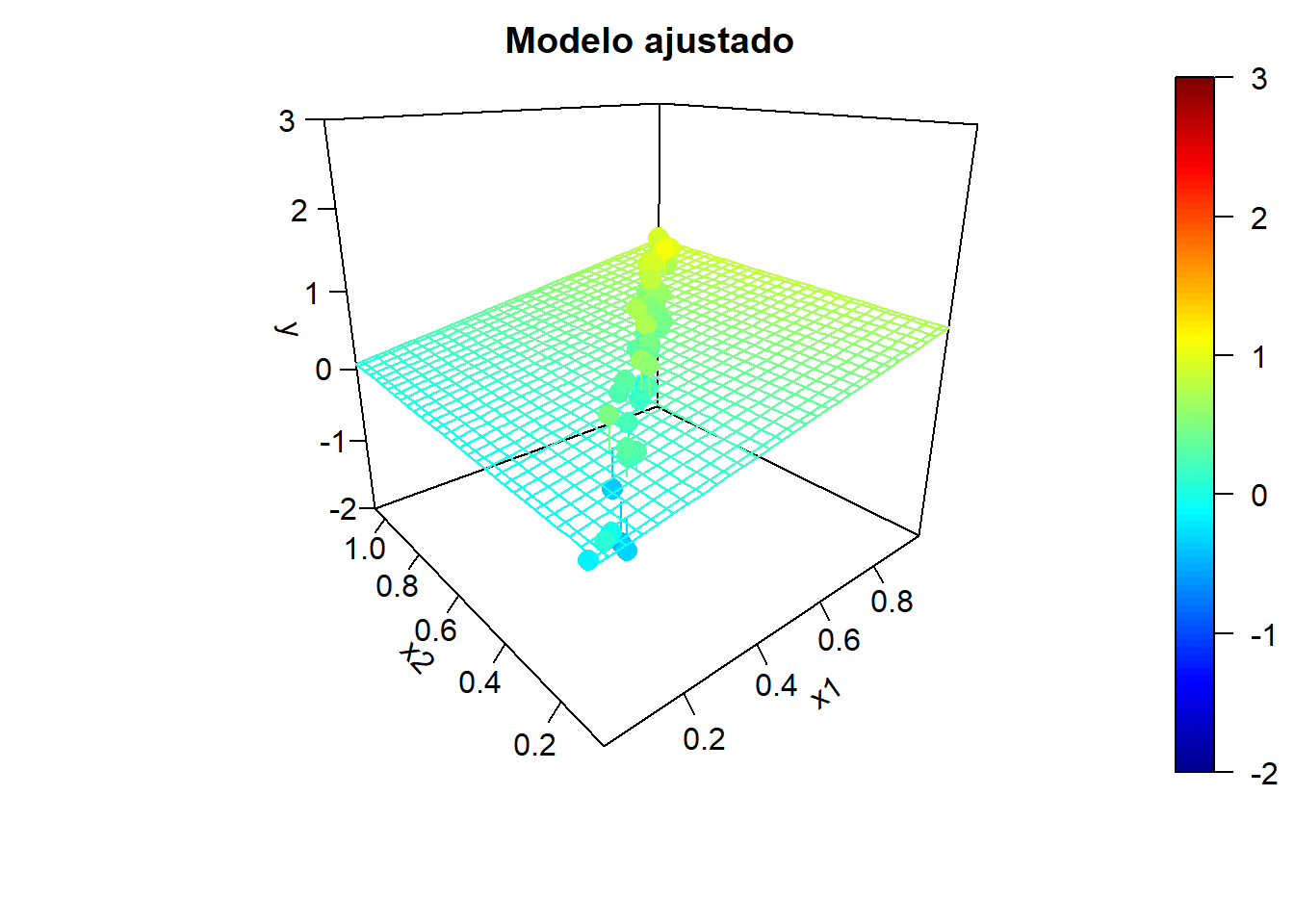 

Figura 2.5: Ejemplo de simulaciones bajo colinelidad y correspondientes modelos ajustados.

Podemos observar una alta variabilidad en los modelos ajustados (puede haber grandes diferencias en las estimaciones de los coeficientes de los predictores). Incluso puede ocurrir que el contraste de regresión sea significativo (alto coeficiente de determinación), pero los contrastes individuales sean no significativos. Por ejemplo, en el último ajuste obtendríamos:

summary(fit)

## 
## Call:
## lm(formula = y ~ x1 + x2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4546 -0.1315  0.0143  0.1632  0.3662 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  -0.1137     0.0894   -1.27     0.21
## x1            0.8708     1.1993    0.73     0.47
## x2            0.1675     1.1934    0.14     0.89
## 
## Residual standard error: 0.221 on 47 degrees of freedom
## Multiple R-squared:  0.631,  Adjusted R-squared:  0.615 
## F-statistic: 40.1 on 2 and 47 DF,  p-value: 6.78e-11

Podemos comparar los resultados anteriores con los obtenidos, también mediante simulación, utilizando predictores incorrelados (ver Figura 2.6). En este caso, el único cambio es generar el segundo predictor de forma independiente:

x2 <- rand.gen(n)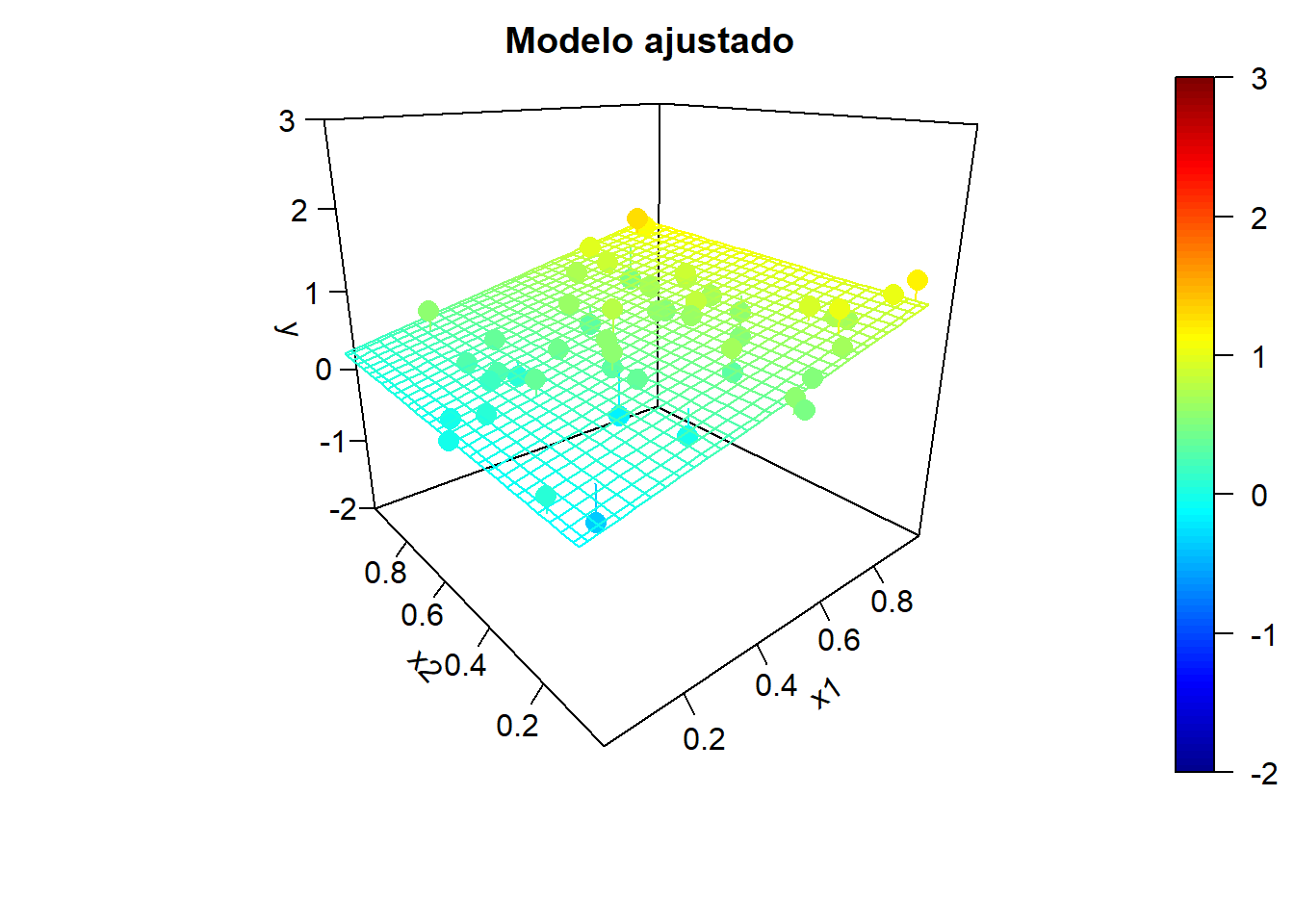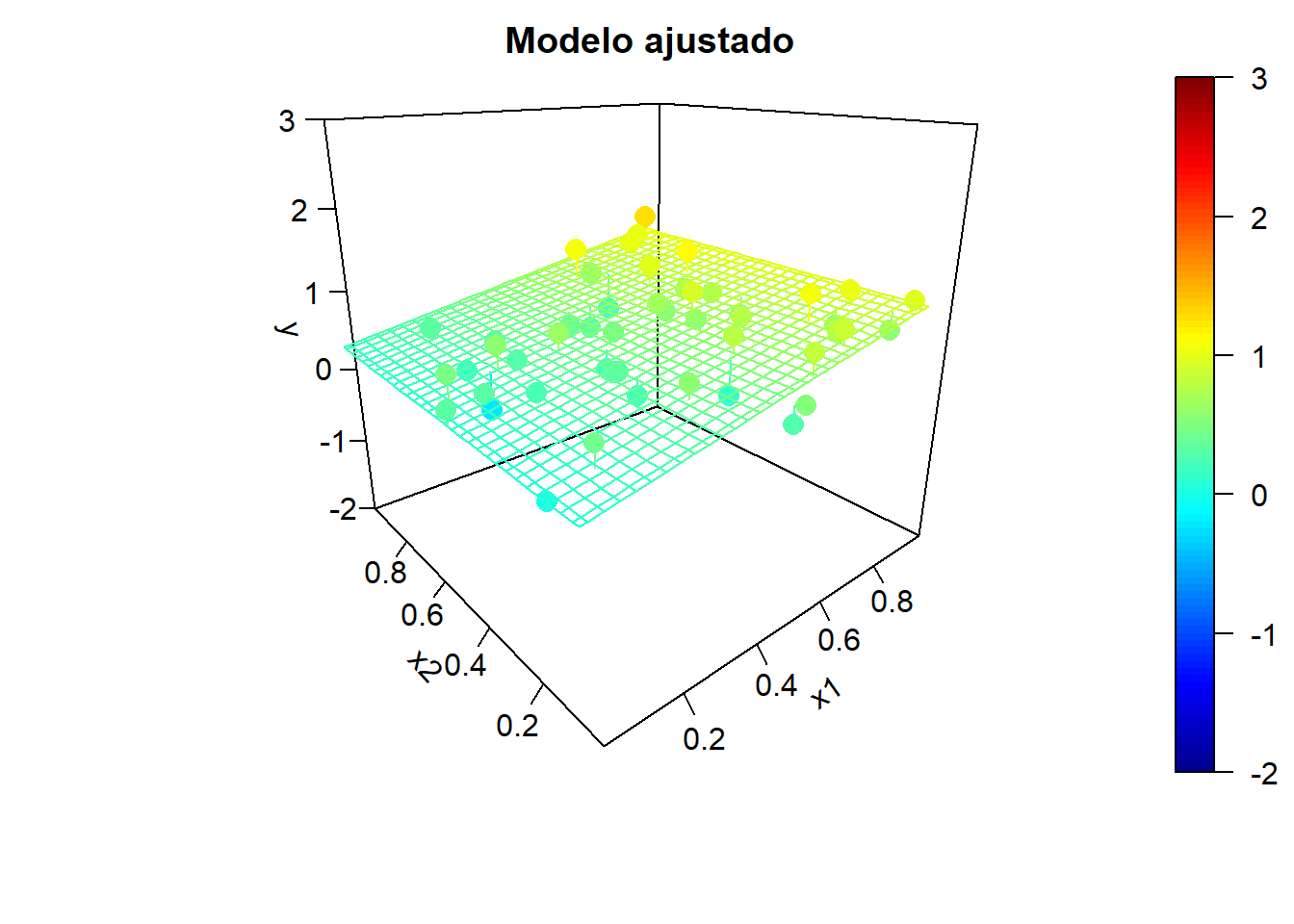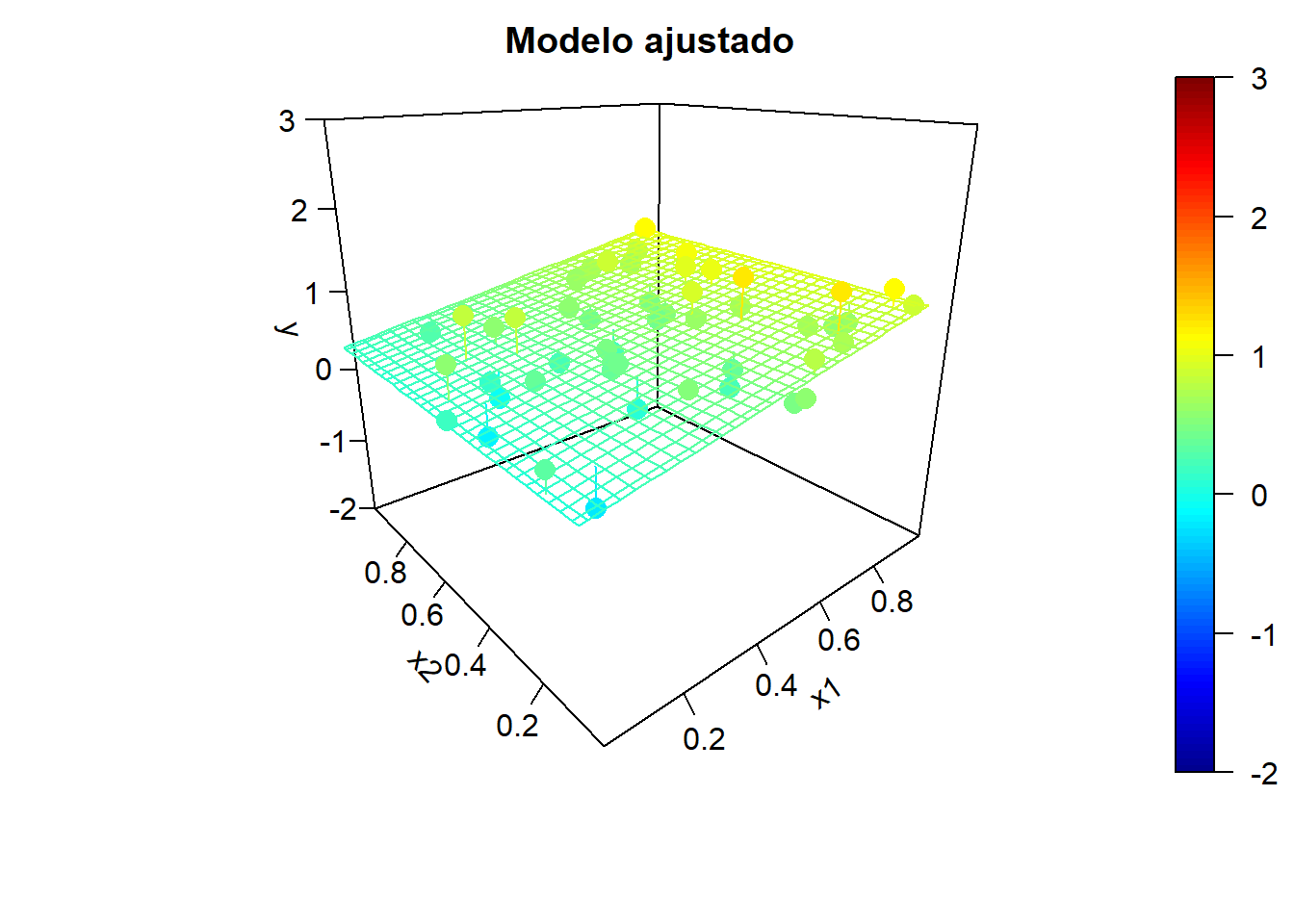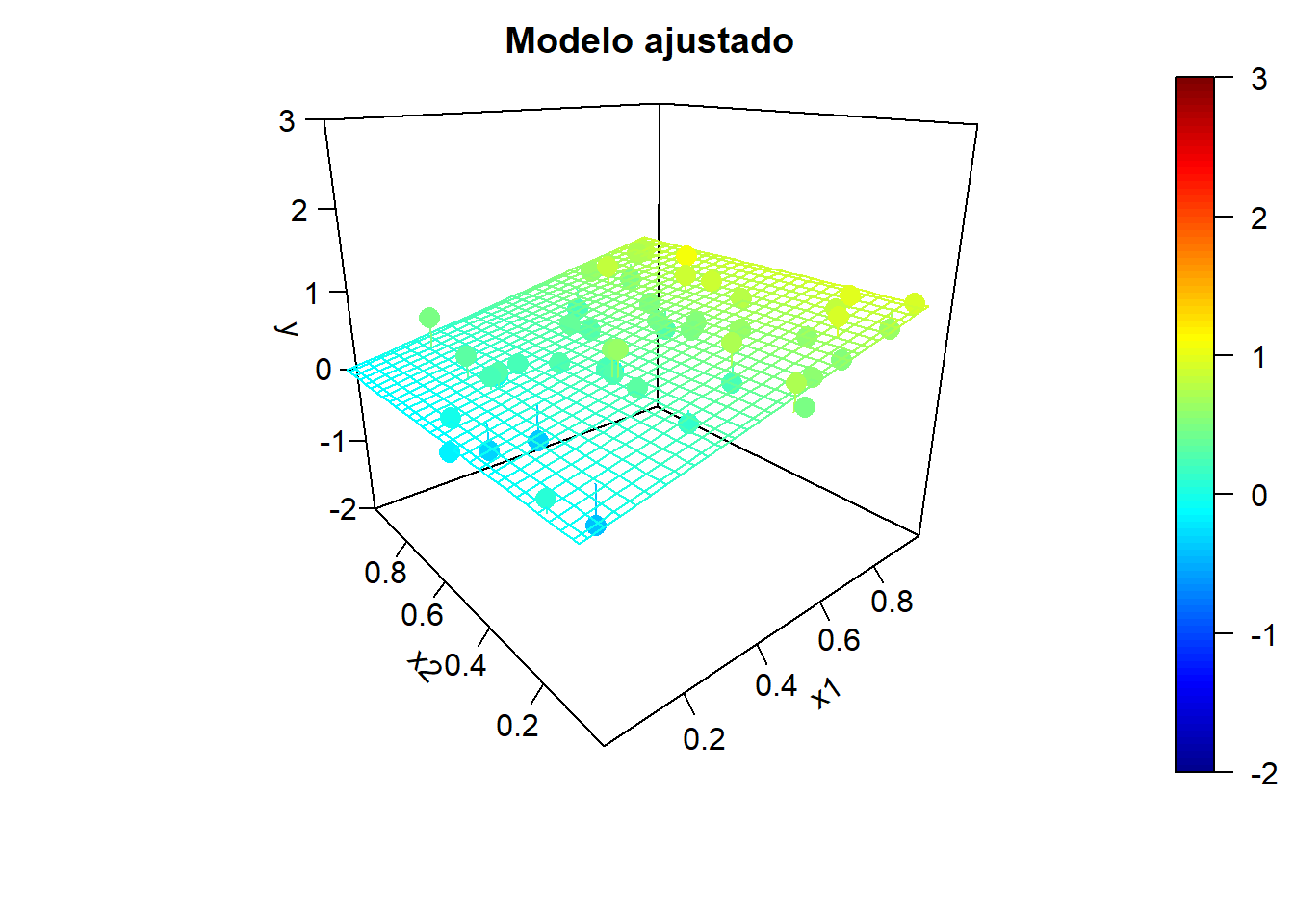 

Figura 2.6: Ejemplo de simulaciones bajo independencia y correspondientes modelos ajustados.

Por ejemplo, en el último ajuste obtendríamos:

summary(fit2)

## 
## Call:
## lm(formula = y ~ x1 + x2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4493 -0.1437  0.0179  0.1532  0.3990 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -0.0777     0.0902   -0.86     0.39    
## x1            1.0371     0.1157    8.97  9.6e-12 ***
## x2           -0.0549     0.1134   -0.48     0.63    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.22 on 47 degrees of freedom
## Multiple R-squared:  0.632,  Adjusted R-squared:  0.617 
## F-statistic: 40.4 on 2 and 47 DF,  p-value: 6.09e-11

En la práctica, para la detección de colinealidad se puede emplear la función vif() del paquete car, que calcula los factores de inflación de la varianza para las variables del modelo. Por ejemplo, en los últimos ajustes obtendríamos:

library(car)
vif(fit)

##     x1     x2 
## 107.08 107.08

vif(fit2) 

##     x1     x2 
## 1.0005 1.0005

La idea de este estadístico es que la varianza de la estimación del efecto en regresión simple (efecto global) es menor que en regresión múltiple (efecto parcial). El factor de inflación de la varianza mide el incremento debido a la colinealidad. Valores grandes, por ejemplo mayores que 10, indican la posible presencia de colinealidad.

Las tolerancias, proporciones de variabilidad no explicada por las demás covariables, se pueden calcular con 1/vif(modelo). Por ejemplo, los coeficientes de tolerancia de los últimos ajustes serían:

1/vif(fit)

##        x1        x2 
## 0.0093387 0.0093387

1/vif(fit2) 

##      x1      x2 
## 0.99947 0.99947

Aunque el factor de inflación de la varianza y la tolerancia son las medidas más utilizadas, son bastante simples y puede ser preferible emplear otras como el índice de condicionamiento, implementado en el paquete mctest.

Como ya se comentó en la Sección 1.4, el problema de la colinealidad se agrava al aumentar el número de dimensiones (la maldición de la dimensionalidad). Hay que tener en cuenta también que, además de la dificultad para interpretar el efecto de los predictores, va a resultar más difícil determinar qué variables son de interés para predecir la respuesta (i. e. no son ruido). Debido a la aleatoriedad, predictores que realmente no están relacionados con la respuesta pueden incluirse en el modelo con mayor facilidad, especialmente si se recurre a los contrastes tradicionales para determinar si tienen un efecto significativo.

2.1.2 Selección de variables explicativas

Cuando se dispone de un conjunto grande de posibles variables explicativas, suele ser especialmente importante determinar cuáles de estas deberían ser incluidas en el modelo de regresión. Solo se deben incluir las variables que contienen información relevante sobre la respuesta, porque así se simplifica la interpretación del modelo, se aumenta la precisión de la estimación y se evitan los problemas de colinealidad. Se trataría entonces de conseguir un buen ajuste con el menor número de predictores posible.

Para obtener el modelo “óptimo” lo ideal sería evaluar todas las posibles combinaciones de los predictores. La función regsubsets() del paquete leaps permite seleccionar los mejores modelos fijando el número máximo de variables explicativas. Por defecto, evalúa todos los modelos posibles con un determinado número de parámetros (variando desde 1 hasta por defecto un máximo de nvmax = 8) y selecciona el mejor (nbest = 1).

library(leaps)
regsel <- regsubsets(bodyfat ~ . , data = train)
# summary(regsel)

Al representar el resultado se obtiene un gráfico con los mejores modelos ordenados según el criterio determinado por el argumento²⁴ scale = c("bic", "Cp", "adjr2", "r2") (para detalles sobre estas medidas, ver por ejemplo la Sección 6.1.3 de James et al., 2021). Se representa una matriz en la que las filas se corresponden con los modelos y las columnas con predictores, indicando los incluidos en cada modelo mediante un sombreado. En la Figura 2.7 se muestra el resultado obtenido empleando el coeficiente de determinación ajustado.

plot(regsel, scale = "adjr2")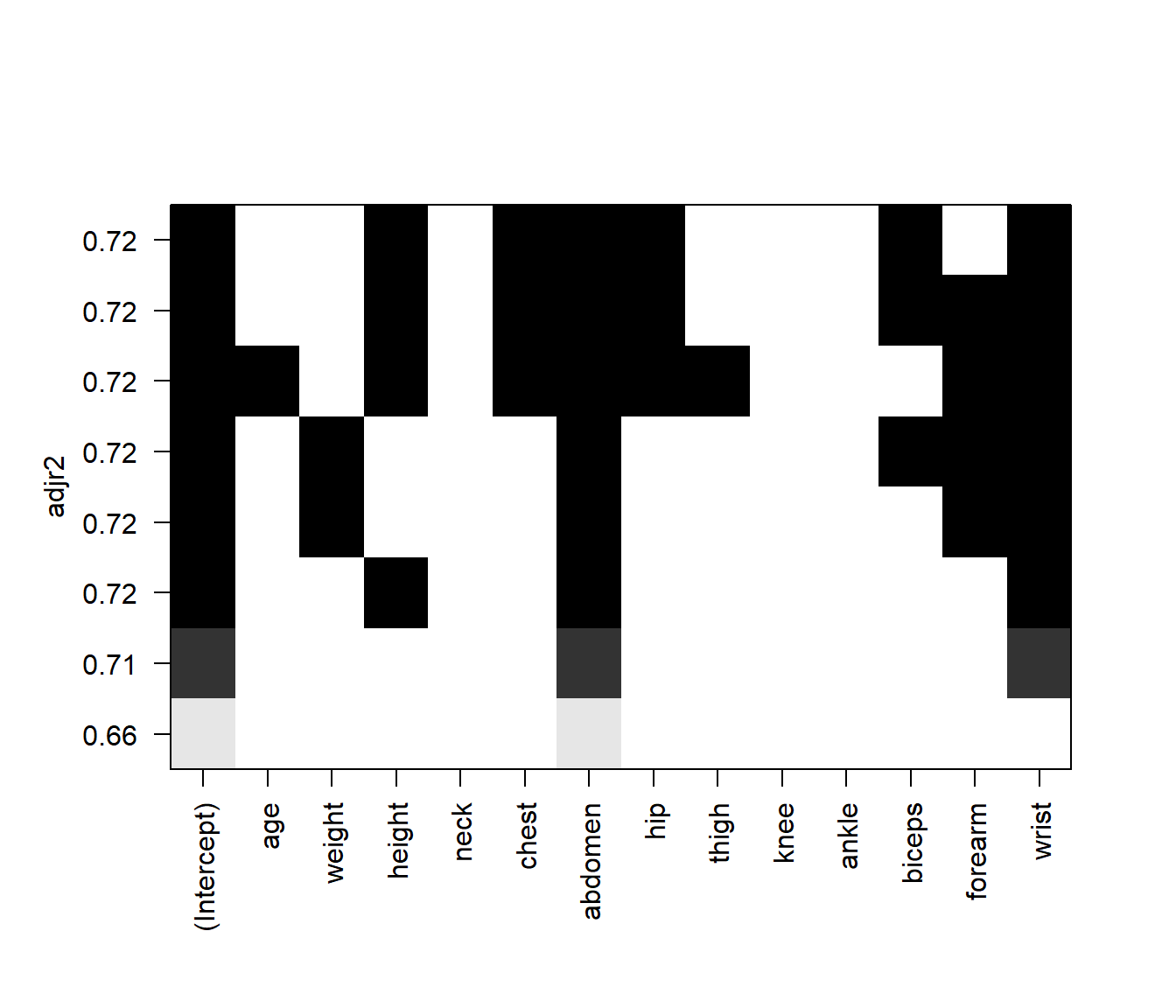

Figura 2.7: Modelos obtenidos mediante búsqueda exhaustiva ordenados según su coeficiente de determinación ajustado.

En este caso, considerando que es preferible un modelo más simple que una mejora del 1 % en la proporción de variabilidad explicada, seleccionamos como modelo final el modelo con dos predictores. Podemos obtener fácilmente los coeficientes de este modelo:

coef(regsel, 2)

## (Intercept)     abdomen       wrist 
##     -9.0578      0.7780     -2.4159

pero suele ser recomendable volver a hacer el ajuste:

modelo <- lm(bodyfat ~ abdomen + wrist, data = train)

Si el número de variables es grande, no resulta práctico evaluar todas las posibilidades. En este caso se suele utilizar alguno (o varios) de los siguientes métodos:

• Selección progresiva (forward): Se parte de una situación en la que no hay ninguna variable y en cada paso se incluye una variable aplicando un criterio de entrada (hasta que ninguna de las restantes lo verifican).

• Eliminación progresiva (backward): Se parte del modelo con todas las variables y en cada paso se elimina una variable aplicando un criterio de salida (hasta que ninguna de las incluidas lo verifican).

• Selección paso a paso (stepwise): Se combina un criterio de entrada y uno de salida. Normalmente se empieza sin ninguna variable y en cada paso puede haber una inclusión y posteriormente la exclusión de alguna de las anteriormente añadidas (forward/backward). Otra posibilidad es partir del modelo con todas las variables, y en cada paso puede haber una exclusión y posteriormente la inclusión de alguna de las anteriormente eliminadas (backward/forward).

Hay que tener en cuenta que se trata de algoritmos “voraces” (greedy, también denominados “avariciosos”), ya que en cada paso tratan de elegir la mejor opción, pero no garantizan que el resultado final sea la solución global óptima (de hecho, es bastante habitual que no coincidan los modelos finales de los distintos métodos, especialmente si el número de observaciones o de variables es grande).

La función stepAIC() del paquete MASS permite seleccionar el modelo por pasos²⁵, hacia delante o hacia atrás según el criterio AIC (Akaike Information Criterion) o BIC (Bayesian Information Criterion). La función stepwise() del paquete RcmdrMisc es una interfaz de stepAIC() que facilita su uso. Los métodos disponibles son "backward/forward", "forward/backward", "backward" y "forward". Normalmente, obtendremos un modelo más simple combinando el método por pasos hacia delante con el criterio BIC:

library(MASS)
library(RcmdrMisc)
modelo.completo <- lm(bodyfat ~ . , data = train)
modelo <- stepwise(modelo.completo, direction = "forward/backward", 
                   criterion = "BIC")

## 
## Direction:  forward/backward
## Criterion:  BIC 
## 
## Start:  AIC=830.6
## bodyfat ~ 1
## 
##           Df Sum of Sq   RSS AIC
## + abdomen  1      8796  4417 621
## + chest    1      6484  6729 704
## + hip      1      5176  8037 738
## + weight   1      5036  8177 742
## + thigh    1      3889  9324 768
## + neck     1      3069 10144 784
## + knee     1      2975 10238 786
## + biceps   1      2895 10317 787
## + forearm  1      1648 11565 810
## + wrist    1      1095 12118 819
## + age      1       699 12514 825
## + ankle    1       600 12612 827
## <none>                 13213 831
## + height   1        11 13201 836
## 
## Step:  AIC=621.13
## bodyfat ~ abdomen
## 
##           Df Sum of Sq   RSS AIC
## + wrist    1       610  3807 597
## + weight   1       538  3879 601
## + height   1       414  4003 607
## + hip      1       313  4104 612
## + ankle    1       293  4124 613
## + neck     1       276  4142 614
## + knee     1       209  4208 617
## + chest    1       143  4274 620
## <none>                  4417 621
## + thigh    1        88  4329 622
## + forearm  1        78  4339 623
## + biceps   1        72  4345 623
## + age      1        56  4362 624
## - abdomen  1      8796 13213 831
## 
## Step:  AIC=597.25
## bodyfat ~ abdomen + wrist
## 
##           Df Sum of Sq   RSS AIC
## + height   1       152  3654 595
## + weight   1       136  3671 595
## + hip      1       113  3694 597
## <none>                  3807 597
## + age      1        74  3733 599
## + ankle    1        31  3776 601
## + knee     1        29  3778 601
## + chest    1        25  3782 601
## + neck     1        17  3790 602
## + thigh    1        14  3793 602
## + forearm  1         5  3802 602
## + biceps   1         2  3805 602
## - wrist    1       610  4417 621
## - abdomen  1      8311 12118 819
## 
## Step:  AIC=594.53
## bodyfat ~ abdomen + wrist + height
## 
##           Df Sum of Sq   RSS AIC
## <none>                  3654 595
## - height   1       152  3807 597
## + hip      1        40  3614 598
## + chest    1        35  3620 598
## + age      1        27  3628 598
## + weight   1        22  3632 599
## + forearm  1        15  3640 599
## + biceps   1         9  3645 599
## + neck     1         9  3646 599
## + ankle    1         2  3652 600
## + knee     1         0  3654 600
## + thigh    1         0  3654 600
## - wrist    1       349  4003 607
## - abdomen  1      8151 11805 819

En la salida de texto de esta función, "<none>" representa el modelo actual en cada paso y se ordenan las posibles acciones dependiendo del criterio elegido (aunque siempre muestra el valor de AIC). El algoritmo se detiene cuando ninguna de ellas mejora el modelo actual. Como resultado devuelve el modelo ajustado final:

summary(modelo)

## 
## Call:
## lm(formula = bodyfat ~ abdomen + wrist + height, data = train)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -9.743 -3.058 -0.393  3.331 10.518 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   9.1567     9.1177    1.00   0.3165    
## abdomen       0.7718     0.0373   20.69  < 2e-16 ***
## wrist        -1.9548     0.4567   -4.28  2.9e-05 ***
## height       -0.1457     0.0515   -2.83   0.0052 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.36 on 192 degrees of freedom
## Multiple R-squared:  0.723,  Adjusted R-squared:  0.719 
## F-statistic:  167 on 3 and 192 DF,  p-value: <2e-16

Cuando el número de variables explicativas es muy grande (o si el tamaño de la muestra es pequeño en comparación), pueden aparecer problemas al emplear los métodos anteriores (incluso pueden no ser aplicables). Una alternativa son los métodos de regularización (ridge regression, LASSO; Sección 6.1) o los de reducción de la dimensión (regresión con componentes principales o mínimos cuadrados parciales; Sección 6.2).

Por otra parte, en los modelos anteriores no se consideraron interacciones entre predictores (para detalles sobre como incluir interacciones en modelos lineales ver, por ejemplo, la Sección 8.6 de Fernández-Casal et al., 2022). Podemos considerar como modelo completo respuesta ~ .*. si deseamos incluir, por ejemplo, los efectos principales y las interacciones de orden 2 de todos los predictores.

En la práctica, es habitual comenzar con modelos aditivos y, posteriormente, estudiar posibles interacciones siguiendo un proceso interactivo. Una posible alternativa consiste en considerar un nuevo modelo completo a partir de las variables seleccionadas en el modelo aditivo, incluyendo todas las posibles interacciones de orden 2, y posteriormente aplicar alguno de los métodos de selección anteriores. Como vimos en el Capítulo 1, en AE interesan algoritmos que puedan detectar e incorporar automáticamente efectos de interacción (en los capítulos siguientes veremos extensiones en este sentido).

2.1.3 Análisis e interpretación del modelo

Además del problema de la colinealidad, si no se verifican las otras hipótesis estructurales del modelo (Sección 2.1), los resultados y las conclusiones basados en la teoría estadística pueden no ser fiables, o incluso totalmente erróneos:

• La falta de linealidad “invalida” las conclusiones obtenidas (hay que tener especial cuidado con las extrapolaciones).

• La falta de normalidad tiene poca influencia si el número de datos es suficientemente grande (justificado, teóricamente, por el teorema central del límite). En caso contrario, la estimación de la varianza, los intervalos de confianza y los contrastes podrían verse afectados.

• Si no hay igualdad de varianzas, los estimadores de los parámetros no son eficientes, pero sí son insesgados. Las varianzas, los intervalos de confianza y los contrastes podrían verse afectados.

• La dependencia entre observaciones puede tener un efecto mucho más grave.

Con el método plot() se pueden generar gráficos de interés para la diagnosis del modelo (ver Figura 2.8):

oldpar <- par(mfrow = c(2,2))
plot(modelo)
par(oldpar)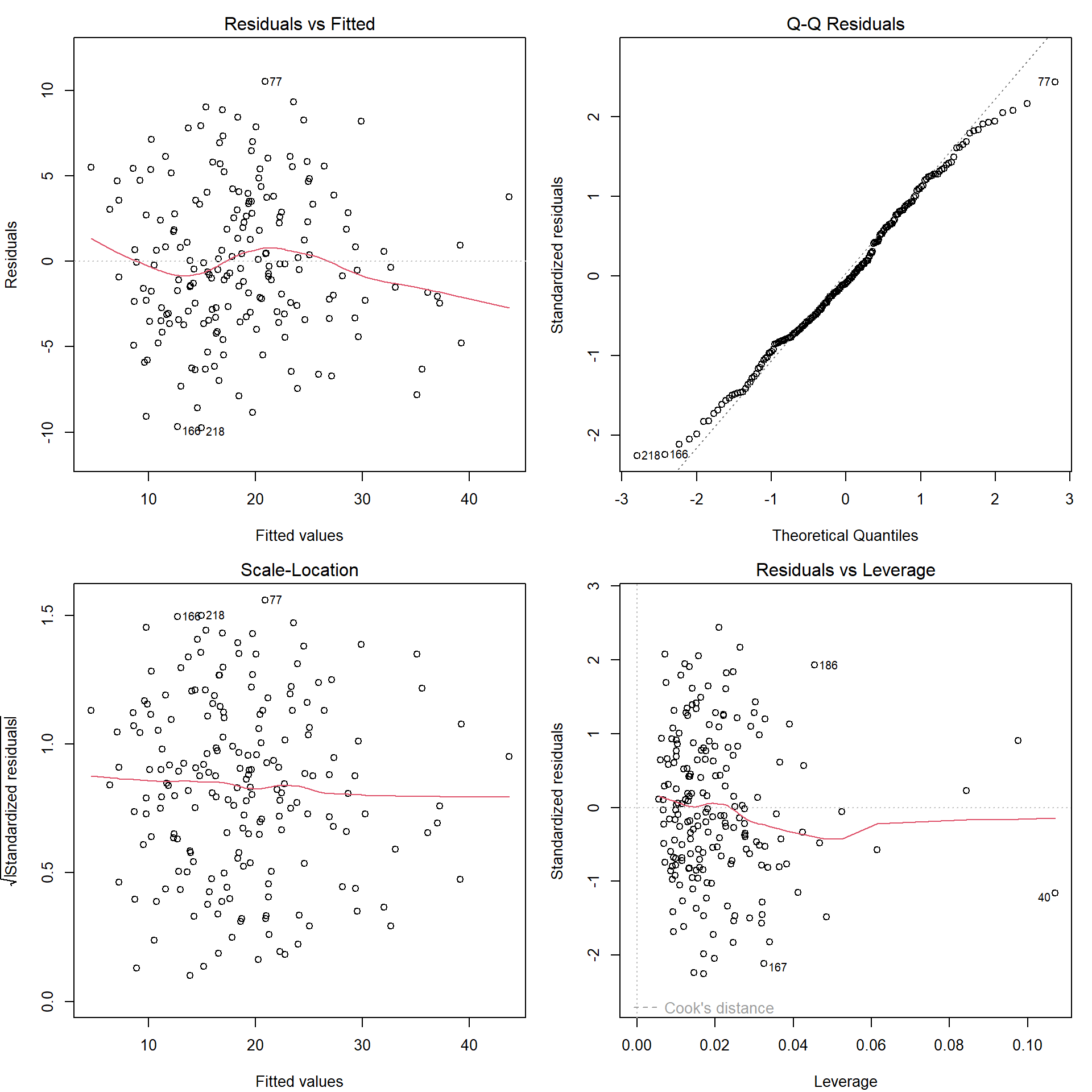

Figura 2.8: Gráficos de diagnóstico del ajuste lineal.

Por defecto se muestran cuatro gráficos (ver help(plot.lm) para más detalles). El primero representa los residuos frente a las predicciones y permite detectar falta de linealidad o heterocedasticidad (o el efecto de un factor omitido: mala especificación del modelo); lo ideal es no observar ningún patrón. En este ejemplo se observa que el modelo podría no ser adecuado para la predicción en valores grandes de la respuesta (aproximadamente a partir de un 30 % de grasa corporal), por lo que se podría pensar en incluir un término cuadrático. El segundo es el gráfico QQ y permite diagnosticar la normalidad; sus puntos deben estar cerca de la diagonal. El tercero es el gráfico de dispersión-nivel y permite detectar la heterocedasticidad y ayudar a seleccionar una transformación para corregirla; la pendiente debe ser nula (como alternativa se puede emplear la función boxcox() del paquete MASS). El último gráfico permite detectar valores atípicos o influyentes; representa los residuos estandarizados en función del valor de influencia (a priori) o leverage²⁶ y señala las observaciones atípicas (residuos fuera del intervalo \([-2,2]\)) e influyentes a posteriori (estadístico de Cook mayor que 0.5 o mayor que 1).

Si las conclusiones obtenidas dependen en gran medida de una observación (normalmente atípica), esta se denomina influyente (a posteriori) y debe ser examinada con cuidado por el experimentador. Se puede volver a ajustar el modelo eliminando las observaciones influyentes²⁷, pero sería recomendable repetir todo el proceso desde la selección de variables. Hay que tener en cuenta que los casos se identifican en los gráficos mediante los nombres de fila de las observaciones, que pueden consultarse con row.names(). Salvo que se hayan definido expresamente, los nombres de fila van a coincidir con los números de fila de los datos originales, en nuestro caso bodyfat, pero no con los números de fila de train. Otra alternativa para evitar la influencia de datos atípicos es emplear regresión lineal robusta, por ejemplo mediante la función rlm() del paquete MASS (ver Ejercicio 2.2).

Es recomendable utilizar gráficos parciales de residuos para analizar los efectos de las variables explicativas y detectar posibles problemas como la falta de linealidad. Se pueden generar con:

termplot(modelo, partial.resid = TRUE)

aunque puede ser preferible emplear las funciones crPlots() ó avPlots() del paquete car²⁸ (ver Figura 2.9):

library(car)
# avPlots(modelo)
crPlots(modelo, main = "")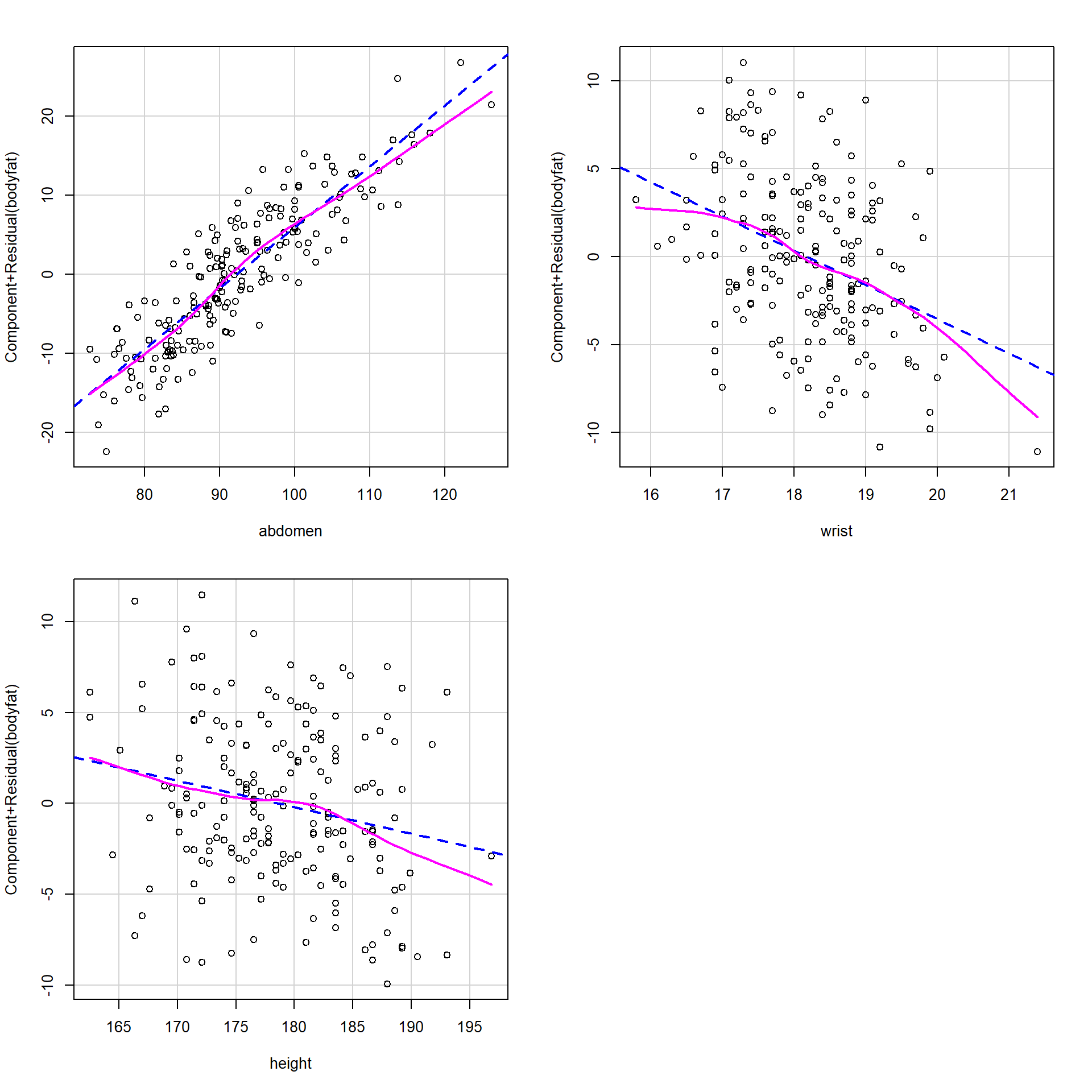

Figura 2.9: Gráficos parciales de residuos (componentes + residuos) del ajuste lineal.

En la tabla 2.2 se incluyen algunas funciones adicionales que permiten obtener medidas de diagnosis o resúmenes numéricos de interés (ver help(influence.measures) para un listado más completo).

Tabla 2.2: Principales funciones para la diagnosis del modelo ajustado.

Función	Descripción
rstandard()	residuos estandarizados (también eliminados)
rstudent()	residuos estudentizados
cooks.distance()	valores del estadístico de Cook
influence()	valores de influencia, cambios en coeficientes y varianza residual al eliminar cada dato (LOOCV)

Hay muchas herramientas adicionales disponibles en otros paquetes, además de las que ya hemos visto de los paquetes car y mctest. Por ejemplo, la librería lmtest proporciona herramientas para la diagnosis de modelos lineales, como el test de Breusch-Pagan para contrastar homocedasticidad, en la función bptest(), o el de Durbin-Watson para detectar si hay correlación en serie²⁹, en la función dwtest().

Cuando no se satisfacen los supuestos básicos del modelo, pueden aplicarse diversas soluciones:

• Pueden llevarse a cabo transformaciones de los datos para tratar de corregir la falta de linealidad, heterocedasticidad y/o normalidad (habitualmente estas últimas “suelen ocurrir en la misma escala”). También se pueden utilizar modelos lineales generalizados (Sección 2.2 y Capítulo 6).

• Si no se logra corregir la heterocedasticidad, puede ser adecuado utilizar mínimos cuadrados ponderados, para lo que habría que modelar la varianza.

• Si hay dependencia, se puede tratar de modelarla y utilizar mínimos cuadrados generalizados.

• Si no se logra corregir la falta de linealidad, se pueden utilizar modelos más flexibles (Capítulo 6 y siguientes).

Una alternativa a las soluciones anteriores es emplear las técnicas de aprendizaje estadístico descritas en la Sección 1.3. Desde este punto de vista, podemos ignorar las hipótesis estructurales y pensar que los procedimientos clásicos, como por ejemplo el ajuste lineal mediante el método por pasos, son simplemente algoritmos de predicción. En ese caso, después de ajustar el modelo en la muestra de entrenamiento, en lugar de emplear medidas como el coeficiente de determinación ajustado, emplearíamos la muestra de test para evaluar la capacidad predictiva en nuevas observaciones.

Una vez obtenido el ajuste final, la ventaja de emplear un modelo lineal es que resultaría muy fácil interpretar el efecto de los predictores en la respuesta a partir de las estimaciones de los coeficientes:

coef(modelo)

## (Intercept)     abdomen       wrist      height 
##     9.15668     0.77181    -1.95482    -0.14570

En este caso abdomen tiene un efecto positivo, mientras que el de wrist y height es negativo (ver Figura 2.9). Por ejemplo, estimaríamos que por cada incremento de un centímetro en la circunferencia del abdomen, el porcentaje de grasa corporal aumentará un 0.77 % (siempre que no varíen los valores de wrist y height). Es importante destacar que estos coeficientes dependen de la escala de las variables y, por tanto, no deberían ser empleados como medidas de importancia de los predictores si sus unidades de medida no son comparables. Es preferible emplear los valores observados de los estadísticos para contrastar si su efecto es significativo (columna t value en el resumen del modelo ajustado):

summary(modelo)$coefficients[-1, 3]

## abdomen   wrist  height 
## 20.6939 -4.2806 -2.8295

ya que son funciones del correspondiente coeficiente de correlación parcial (la correlación entre la respuesta y el predictor después de eliminar el efecto lineal del resto de predictores). Alternativamente, se pueden emplear los denominados coeficientes estandarizados o pesos beta, por ejemplo mediante la función scaled.coef() del paquete mpae:

scaled.coef(modelo) # scale.response = TRUE

##  abdomen    wrist   height 
##  0.95710 -0.21157 -0.11681

Estos coeficientes serían los obtenidos al ajustar el modelo tipificando previamente todas las variables³⁰. Tanto el valor absoluto de estos coeficientes como el de los estadísticos de contraste se podrían considerar medidas de la importancia de los predictores.

2.1.4 Evaluación de la precisión

Para evaluar la precisión de las predicciones se puede utilizar el coeficiente de determinación ajustado:

summary(modelo)$adj.r.squared

## [1] 0.71909

que estima la proporción de variabilidad explicada en una nueva muestra. Sin embargo, hay que tener en cuenta que su validez depende de las hipótesis estructurales (especialmente de la linealidad, homocedasticidad e independencia), ya que se obtiene a partir de estimaciones de las varianzas residual y total:

\[R_{ajus}^{2} = 1 - \frac{\hat{S}_{R}^{2}}{\hat{S}_{Y}^{2}} = 1 - \left( \frac{n-1}{n-p-1} \right) (1-R^{2})\]

siendo \(\hat{S}_{R}^{2}=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}/(n - p - 1)\). Algo similar ocurre con otras medidas de bondad de ajuste, como por ejemplo BIC o AIC.

Alternativamente, si no es razonable asumir estas hipótesis, se puede emplear el procedimiento tradicional en AE (o alguno de los otros descritos en la Sección 1.3).

Podemos evaluar el modelo ajustado en el conjunto de datos de test y comparar las predicciones frente a los valores reales (como se mostró en la Sección 1.3.4; ver Figura 2.10). En este caso, se observa una infrapredicción en valores grandes de la respuesta, especialmente en torno al 20 % de grasa corporal (como ya se ha visto en la diagnosis realizada en la sección anterior, aparentemente se debería haber incluido un término cuadrático).

obs <- test$bodyfat
pred <- predict(modelo, newdata = test)
pred.plot(pred, obs, xlab = "Predicción", ylab = "Observado")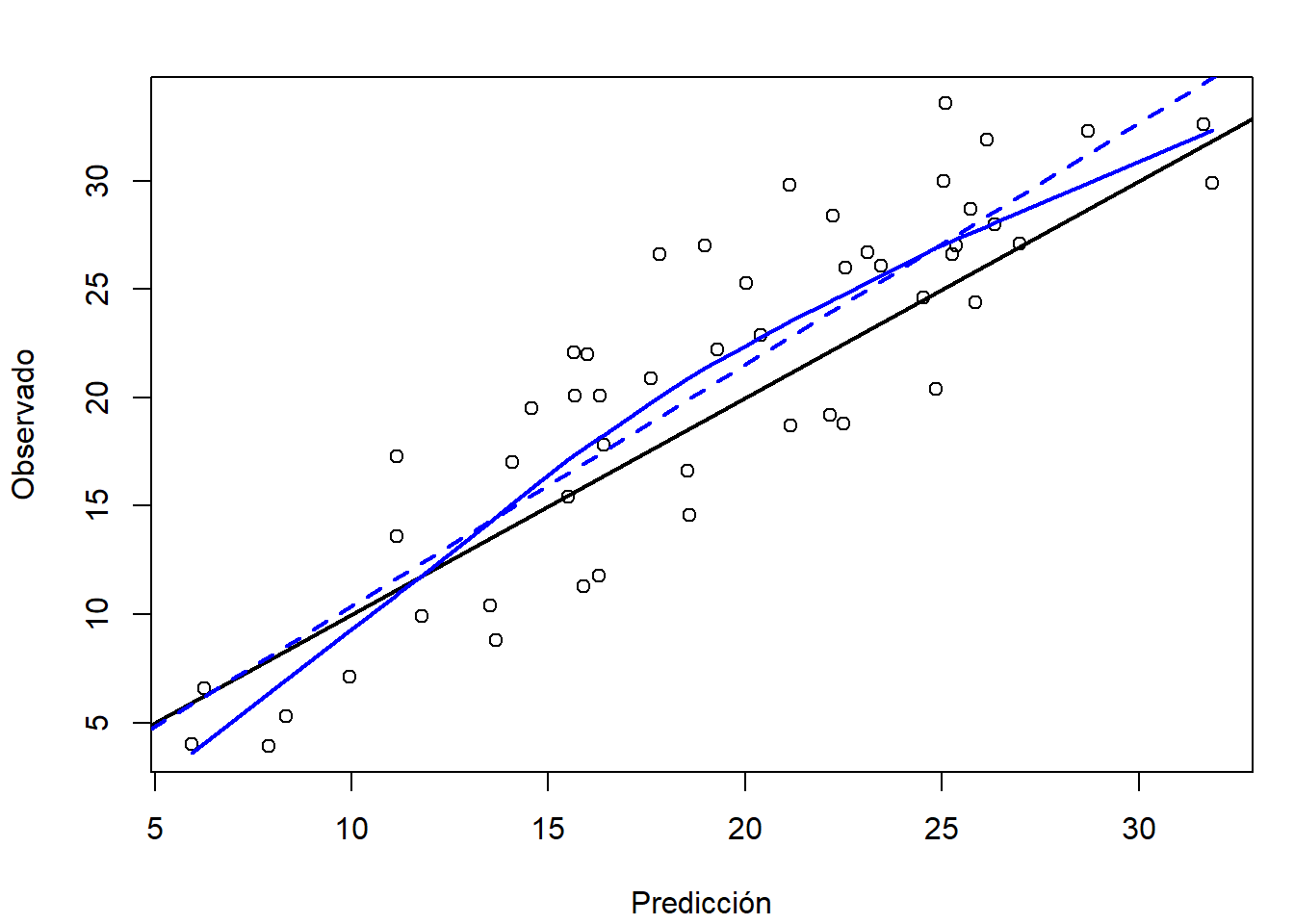

Figura 2.10: Gráfico de dispersión de observaciones frente a predicciones, del ajuste lineal en la muestra de test.

También podemos obtener medidas de error:

accuracy(pred, obs)

##        me      rmse       mae       mpe      mape r.squared 
##   1.44076   4.19456   3.59129  -0.68191  21.46643   0.72802

Ejercicio 2.2 El conjunto de datos mpae::bodyfat.raw contiene observaciones adicionales en las que se sospecha que hubo errores en las mediciones o en la introducción de datos. Particiona estos datos en una muestra de entrenamiento y una de test, ajusta el modelo anterior mediante regresión robusta con la función MASS::rlm():

rlm(bodyfat ~ abdomen + wrist + height, data = train)

evalúa las predicciones en la muestra de test y compara los resultados con los del ejemplo anterior.

2.1.5 Selección del modelo mediante remuestreo

Los métodos de selección de variables descritos en la Sección 2.1.2 también dependen, en mayor o menor medida, de la validez de las hipótesis estructurales. Por este motivo se podría pensar en emplear alguno de los procedimientos descritos en la Sección 1.3. Por ejemplo, podríamos considerar como hiperparámetros la inclusión, o no, de cada una de las posibles variables explicativas y realizar la selección de variables (la complejidad del modelo) mediante remuestreo (ver bestglm::bestglm(..., IC = c("LOOCV", "CV"))). Sin embargo, esto puede presentar dificultades computacionales.

Otra posibilidad es emplear remuestreo para escoger entre distintos procedimientos de selección o para escoger el número de predictores incluidos en el modelo. En este caso, el procedimiento de selección debería realizarse también en cada uno de los conjuntos de entrenamiento utilizados en la validación. Esto último puede hacerse fácilmente con el paquete caret. Este paquete implementa métodos de selección basados en el paquete leaps, considerando el número máximo de predictores nvmax como hiperparámetro y empleando búsqueda: hacia atrás ("leapBackward"), hacia delante ("leapForward") y por pasos ("leapSeq").

library(caret)
modelLookup("leapSeq")

##     model parameter                        label forReg forClass probModel
## 1 leapSeq     nvmax Maximum Number of Predictors   TRUE    FALSE     FALSE

caret.leapSeq <- train(bodyfat ~ ., data = train, method = "leapSeq",
                       trControl = trainControl(method = "cv", number = 10),
                       tuneGrid = data.frame(nvmax = 1:6))
caret.leapSeq

## Linear Regression with Stepwise Selection 
## 
## 196 samples
##  13 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 176, 176, 178, 175, 178, 176, ... 
## Resampling results across tuning parameters:
## 
##   nvmax  RMSE    Rsquared  MAE   
##   1      4.6868  0.67536   3.8501
##   2      4.3946  0.71180   3.6432
##   3      4.3309  0.72370   3.5809
##   4      4.5518  0.69680   3.7780
##   5      4.4163  0.71225   3.6770
##   6      4.4015  0.71020   3.6674
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was nvmax = 3.

# summary(caret.leapSeq$finalModel)
with(caret.leapSeq, coef(finalModel, bestTune$nvmax))

## (Intercept)      height     abdomen       wrist 
##     9.15668    -0.14570     0.77181    -1.95482

Una vez seleccionado el modelo final³¹, estudiaríamos la eficiencia de las predicciones en la muestra de test:

pred <- predict(caret.leapSeq, newdata = test)
accuracy(pred, obs)

##        me      rmse       mae       mpe      mape r.squared 
##   1.44076   4.19456   3.59129  -0.68191  21.46643   0.72802

Además, en el caso de ajustes de modelos de este tipo, puede resultar de interés realizar un preprocesado de los datos para eliminar predictores correlados o con varianza próxima a cero, estableciendo por ejemplo preProc = c("nzv", "corr") en la llamada a la función train().

Bibliografía

Fernández-Casal, R., Roca-Pardiñas, J., Costa, J., y Oviedo-de la Fuente, M. (2022). Introducción al Análisis de Datos con R. https://rubenfcasal.github.io/intror.

James, G., Witten, D., Hastie, T., y Tibshirani, R. (2021). An Introduction to Statistical Learning: With Applications in R (2a. ed.). Springer. https://www.statlearning.com. https://www.statlearning.com

Penrose, K. W., Nelson, A., y Fisher, A. (1985). Generalized body composition prediction equation for men using simple measurement techniques. Medicine & Science in Sports & Exercise, 17(2), 189. https://doi.org/10.1249/00005768-198504000-00037

---

23. Algunos predictores podrían corresponderse con interacciones, \(X_i = X_j X_k\), o transformaciones (p. ej. \(X_i = X_j^2\)) de las variables explicativas originales. También se podría haber transformado la respuesta.↩︎

24. Con los criterios habituales, el mejor modelo con un número de variables prefijado no depende del criterio empleado. Aunque estos criterios pueden diferir al comparar modelos con distinto número de predictores.↩︎

25. También está disponible la función step() del paquete base stats con menos opciones. Además de búsqueda exhaustiva, la función leaps::regsubsets() también permite emplear un criterio por pasos, mediante el argumento method = c("backward", "forward", "seqrep"), pero puede ser recomendable usar las otras alternativas para obtener directamente el modelo final.↩︎

26. La influencia a priori (leverage) depende de los valores de las variables explicativas, y cuando es mayor que \(2(p+1)/2\) se considera que la observación está muy alejada del centro de los datos.↩︎

27. Normalmente se sigue un proceso iterativo, eliminando la más influyente cada vez, por ejemplo con which.max(cooks.distance(modelo)) y update().↩︎

28. Estas funciones también permitirían detectar observaciones atípicas o influyentes mediante el argumento id (como se muestra en la Sección 2.2.2).↩︎

29. Para diagnosticar si hay problemas de dependencia temporal sería importante mantener el orden original de recogida de los datos. En este caso no tendría sentido hacerlo con la muestra de entrenamiento, ya que al particionar los datos se seleccionaron las observaciones aleatoriamente (habría que emplear el conjunto de datos original o generar la muestra de entrenamiento teniendo en cuenta la posible dependencia).↩︎

30. Por tanto, no tienen unidades y se interpretarían como el cambio en desviaciones estándar de la variable dependiente al aumentar el correspondiente predictor en una desviación estándar.↩︎

31. Se podrían haber entrenado distintos métodos de selección de predictores y comparar los resultados (en las mismas muestras de validación) para escoger el modelo final.↩︎