7.5 Projection pursuit

Projection pursuit (Friedman y Tukey, 1974) es una técnica de análisis exploratorio de datos multivariantes que busca proyecciones lineales de los datos en espacios de dimensión baja, siguiendo una idea originalmente propuesta en Kruskal (1969). Inicialmente se presentó como una técnica gráfica y por ese motivo buscaba proyecciones de dimensión 1 o 2 (proyecciones en rectas o planos), resultando que las direcciones interesantes son aquellas con distribución no normal. La motivación es que cuando se realizan transformaciones lineales lo habitual es que el resultado tenga la apariencia de una distribución normal (por el teorema central del límite), lo cual oculta las singularidades de los datos originales. Se supone que los datos son una trasformación lineal de componentes no gaussianas (variables latentes) y la idea es deshacer esta transformación mediante la optimización de una función objetivo, que en este contexto recibe el nombre de projection index. Aunque con orígenes distintos, projection pursuit es muy similar a independent component analysis (Comon, 1994), una técnica de reducción de la dimensión que, en lugar de buscar como es habitual componentes incorreladas (ortogonales), busca componentes independientes y con distribución no normal (ver por ejemplo la documentación del paquete fastICA, Marchini et al., 2021).

Hay extensiones de projection pursuit para regresión, clasificación, estimación de la función de densidad, etc.

7.5.1 Regresión por projection pursuit

En el método original de projection pursuit regression (PPR, Friedman y Stuetzle, 1981) se considera el siguiente modelo semiparamétrico \[m(\mathbf{x}) = \sum_{m=1}^M g_m (\alpha_{1m}x_1 + \alpha_{2m}x_2 + \ldots + \alpha_{pm}x_p)\] siendo \(\boldsymbol{\alpha}_m = (\alpha_{1m}, \alpha_{2m}, \ldots, \alpha_{pm})\) vectores de parámetros (desconocidos) de módulo unitario y \(g_m\) funciones suaves (desconocidas), denominadas funciones ridge.

Con esta aproximación se obtiene un modelo muy general que evita los problemas de la maldición de la dimensionalidad. De hecho, se trata de un aproximador universal: con \(M\) suficientemente grande y eligiendo adecuadamente las componentes se podría aproximar cualquier función continua. Sin embargo, el modelo resultante puede ser muy difícil de interpretar, salvo en el caso de \(M=1\), que se corresponde con el denominado single index model empleado habitualmente en econometría, pero que solo es algo más general que el modelo de regresión lineal múltiple.

El ajuste se este tipo de modelos es en principio un problema muy complejo. Hay que estimar las funciones univariantes \(g_m\) (utilizando un método de suavizado) y los parámetros \(\alpha_{im}\), utilizando como criterio de error \(\mbox{RSS}\). En la práctica, se resuelve utilizando un proceso iterativo en el que se van fijando sucesivamente los valores de los parámetros y las funciones ridge (si son estimadas empleando un método que también proporcione estimaciones de su derivada, las actualizaciones de los parámetros se pueden obtener por mínimos cuadrados ponderados).

También se han desarrollado extensiones del método original para el caso de respuesta multivariante: \[m_i(\mathbf{x}) = \beta_{i0} + \sum_{m=1}^M \beta_{im} g_m (\alpha_{1m}x_1 + \alpha_{2m}x_2 + \ldots + \alpha_{pm}x_p)\] reescalando las funciones rigde de forma que tengan media cero y varianza unidad sobre las proyecciones de las observaciones.

Este procedimiento de regresión está muy relacionado con las redes de neuronas artificiales que han sido objeto de mayor estudio y desarrollo en los últimos años. Estos métodos se tratarán en el Capítulo 8.

7.5.2 Implementación en R

El método PPR (con respuesta multivariante) está implementado en la función ppr() del paquete base⁶⁷ de R, y es también la empleada por el método "ppr" de caret:

ppr(formula, data, nterms, max.terms = nterms, optlevel = 2,
    sm.method = c("supsmu", "spline", "gcvspline"),
    bass = 0, span = 0, df = 5, gcvpen = 1, ...)

Esta función va añadiendo términos ridge hasta un máximo de max.terms y posteriormente emplea un método hacia atrás para seleccionar nterms (el argumento optlevel controla cómo se vuelven a reajustar los términos en cada iteración). Por defecto, emplea el super suavizador de Friedman (función supsmu(), con parámetros bass y span), aunque también admite splines (función smooth.spline(), fijando los grados de libertad con df o seleccionándolos mediante GCV). Para más detalles, ver help(ppr).

A continuación, retomamos el ejemplo del conjunto de datos earth::Ozone1. En primer lugar ajustamos un modelo PPR con dos términos (incrementando el suavizado por defecto de supsmu() siguiendo la recomendación de Venables y Ripley, 2002):

ppreg <- ppr(O3 ~ ., nterms = 2, data = train, bass = 2)

Si realizamos un resumen del resultado, se muestran las estimaciones de los coeficientes \(\alpha_{jm}\) de las proyecciones lineales y de los coeficientes \(\beta_{im}\) de las componentes rigde, que podrían interpretarse como una medida de su importancia. En este caso, la primera componente no paramétrica es la que tiene mayor peso en la predicción.

summary(ppreg)

## Call:
## ppr(formula = O3 ~ ., data = train, nterms = 2, bass = 2)
## 
## Goodness of fit:
## 2 terms 
##  4033.7 
## 
## Projection direction vectors ('alpha'):
##          term 1     term 2    
## vh       -0.0166178  0.0474171
## wind     -0.3178679 -0.5442661
## humidity  0.2384546 -0.7864837
## temp      0.8920518 -0.0125634
## ibh      -0.0017072 -0.0017942
## dpg       0.0334769  0.2859562
## ibt       0.2055363  0.0269849
## vis      -0.0262552 -0.0141736
## doy      -0.0448190 -0.0104052
## 
## Coefficients of ridge terms ('beta'):
## term 1 term 2 
## 6.7904 1.5312

Podemos representar las funciones rigde con método plot() (ver Figura 7.23):

plot(ppreg)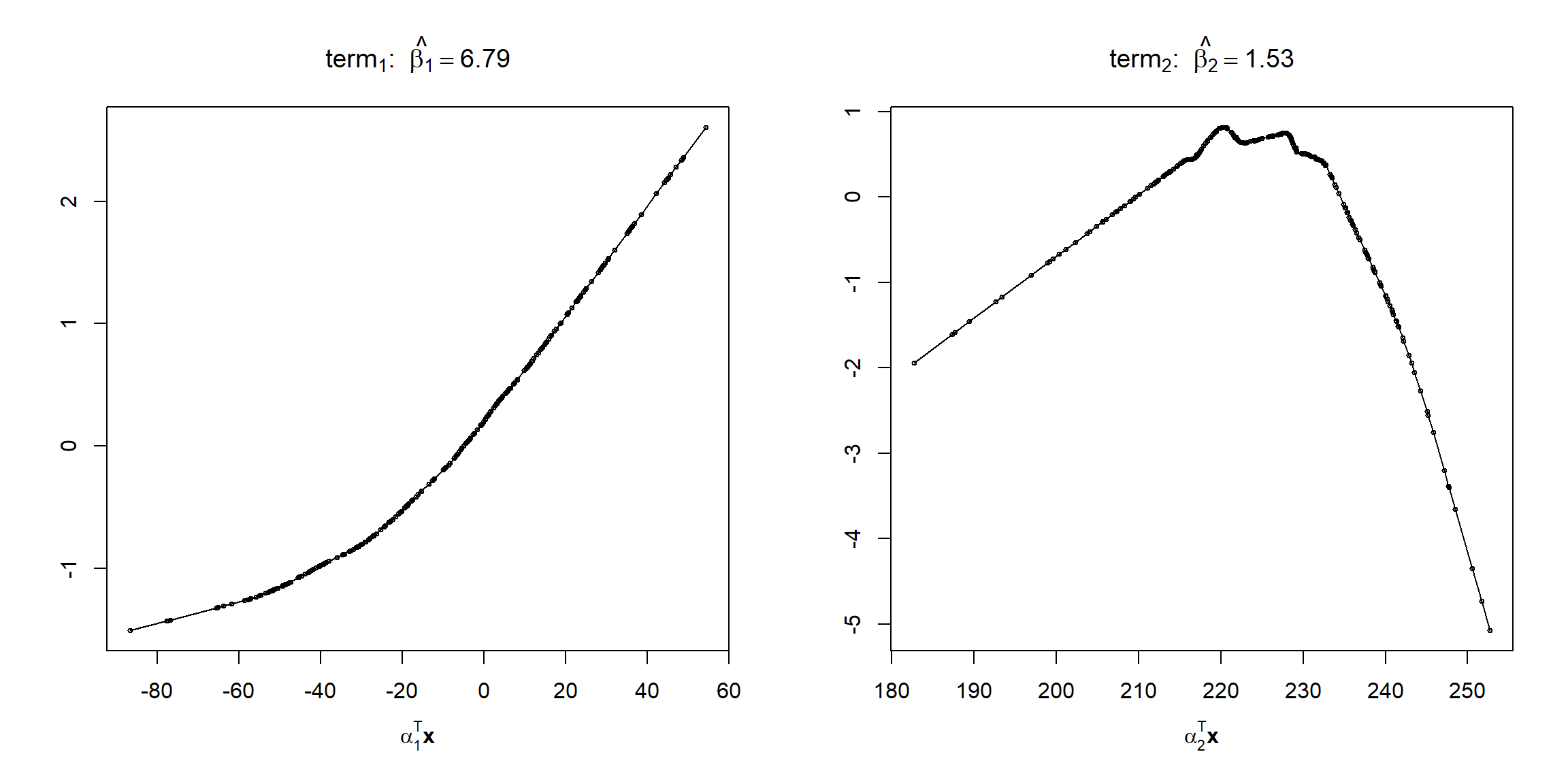

Figura 7.23: Estimaciones de las funciones ridge del ajuste PPR.

En este caso, se estimaría que la primera componente lineal tiene aproximadamente un efecto cuadrático positivo, con un incremento en la pendiente a partir de un valor en torno a \(-30\), y la segunda un efecto cuadrático con un cambio de pendiente de positivo a negativo en torno a 225.

Por último evaluamos las predicciones en la muestra de test:

pred <- predict(ppreg, newdata = test)
obs <- test$O3
accuracy(pred, obs)

##        me      rmse       mae       mpe      mape r.squared 
##   0.48198   3.23301   2.59415  -6.12031  34.87285   0.83846

Empleamos también el método "ppr" de caret para seleccionar automáticamente el número de términos:

library(caret)
modelLookup("ppr")

##   model parameter   label forReg forClass probModel
## 1   ppr    nterms # Terms   TRUE    FALSE     FALSE

set.seed(1)
caret.ppr <- train(O3 ~ ., data = train, method = "ppr", 
                   trControl = trainControl(method = "cv", number = 10))
caret.ppr

## Projection Pursuit Regression 
## 
## 264 samples
##   9 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 238, 238, 238, 236, 237, 239, ... 
## Resampling results across tuning parameters:
## 
##   nterms  RMSE    Rsquared  MAE   
##   1       4.3660  0.70690   3.3067
##   2       4.4793  0.69147   3.4549
##   3       4.6249  0.66441   3.5689
## 
## RMSE was used to select the optimal model using the smallest value.
## The final value used for the model was nterms = 1.

En este caso, se selecciona un único término ridge. Podríamos analizar el modelo final ajustado de forma análoga (ver Figura 7.24):

summary(caret.ppr$finalModel)

## Call:
## ppr(x = as.matrix(x), y = y, nterms = param$nterms)
## 
## Goodness of fit:
## 1 terms 
##  4436.7 
## 
## Projection direction vectors ('alpha'):
##         vh       wind   humidity       temp        ibh        dpg 
## -0.0160915 -0.1678913  0.3517739  0.9073015 -0.0018289  0.0269015 
##        ibt        vis        doy 
##  0.1480212 -0.0264704 -0.0357039 
## 
## Coefficients of ridge terms ('beta'):
## term 1 
##  6.854

plot(caret.ppr$finalModel)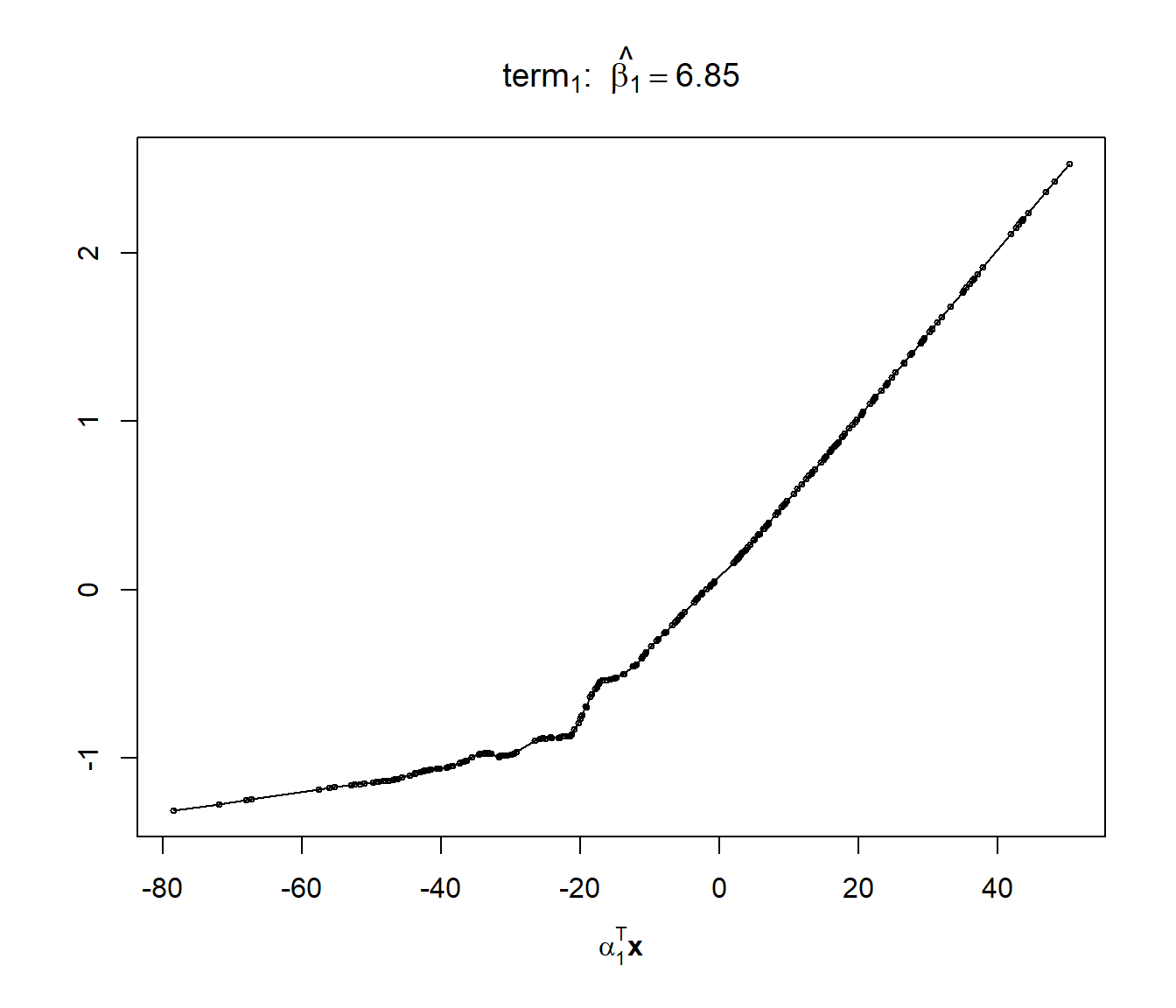 

Figura 7.24: Estimación de la función ridge del ajuste PPR (con selección óptima del número de componentes).

Si estudiamos las predicciones en la muestra de test, la proporción de variabilidad explicada es similar a la obtenida anteriormente con dos componentes ridge:

pred <- predict(caret.ppr, newdata = test)
accuracy(pred, obs)

##        me      rmse       mae       mpe      mape r.squared 
##   0.31359   3.36529   2.70616 -10.75327  33.83336   0.82497

Para ajustar un modelo single index también se podría emplear la función npindex() del paquete np (que implementa el método de Ichimura, 1993, considerando un estimador local constante), aunque en este caso ni el tiempo de computación ni el resultado es satisfactorio⁶⁸:

library(np)
formula <- O3 ~ vh + wind + humidity + temp + ibh + dpg + ibt + vis + doy
bw <- npindexbw(formula, data = train, optim.method = "BFGS", nmulti = 1) 

sindex <- npindex(bws = bw, gradients = TRUE)
summary(sindex)

## 
## Single Index Model
## Regression Data: 264 training points, in 9 variable(s)
## 
##       vh  wind humidity  temp     ibh    dpg    ibt      vis     doy
## Beta:  1 10.85   6.2642 8.856 0.09266 4.0038 5.6625 -0.66145 -1.1185
## Bandwidth: 13.797
## Kernel Regression Estimator: Local-Constant
## 
## Residual standard error: 3.2614
## R-squared: 0.83391
## 
## Continuous Kernel Type: Second-Order Gaussian
## No. Continuous Explanatory Vars.: 1

Al representar la función ridge se observa que, aparentemente, la ventana seleccionada produce un infrasuavizado (sobreajuste; ver Figura 7.25):

plot(bw)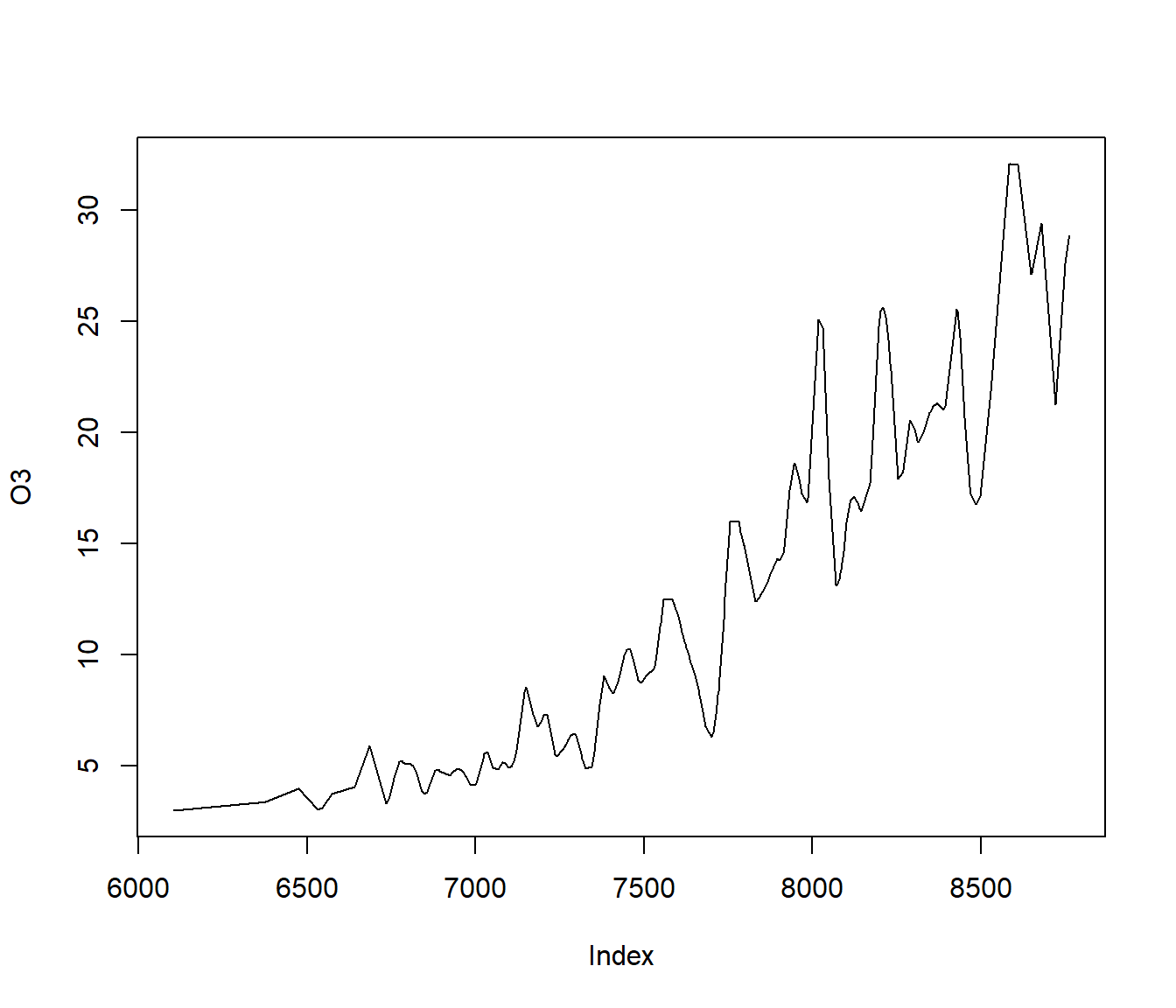

Figura 7.25: Estimación de la función ridge del modelo single index ajustado.

Si analizamos la eficiencia de las predicciones en la muestra de test, la proporción de variabilidad explicada es mucho menor que la del modelo ajustado con la función ppr():

pred <- predict(sindex, newdata = test)
accuracy(pred, obs)

##        me      rmse       mae       mpe      mape r.squared 
##   0.35026   4.77239   3.63679  -8.82255  38.24191   0.64801

Ejercicio 7.9 Continuando con los ejercicios 7.6 y 7.7 anteriores, con los datos de grasa corporal mpae::bodyfat, ajusta un modelo de regresión por projection pursuit empleando el método "ppr" de caret, seleccionando el número de términos ridge nterms = 1:2 y fijando el suavizado máximo bass = 10. Obtén los coeficientes del modelo, representa las funciones ridge y evalúa las predicciones en la muestra de test (gráfico y medidas de error). Comparar los resultados con los obtenidos en los ejercicios anteriores.

Bibliografía

Comon, P. (1994). Independent component analysis, a new concept? Signal Processing, 36(3), 287-314. https://doi.org/10.1016/0165-1684(94)90029-9

Friedman, J., y Stuetzle, W. (1981). Projection pursuit regression. Journal of the American Statistical Association, 76(376), 817-823. https://doi.org/10.1080/01621459.1981.10477729

Friedman, J., y Tukey, J. (1974). A projection pursuit algorithm for exploratory data analysis. IEEE Transactions on computers, 100(9), 881-890. https://doi.org/10.1109/t-c.1974.224051

Ichimura, H. (1993). Semiparametric least squares (SLS) and weighted SLS estimation of single-index models. Journal of Econometrics, 58(1), 71-120. https://doi.org/10.1016/0304-4076(93)90114-K

Kruskal, J. B. (1969). Toward a practical method which helps uncover the structure of a set of multivariate observations by finding the linear transformation which optimizes a new «index of condensation». Statistical Computation, 427-440. https://doi.org/10.1016/b978-0-12-498150-8.50024-0

Marchini, J. L., Heaton, C., y Ripley, B. D. (2021). fastICA: FastICA Algorithms to Perform ICA and Projection Pursuit. https://cran.r-project.org/package=fastICA

Venables, W. N., y Ripley, B. D. (2002). Modern Applied Statistics with S (4a. ed.). Springer. https://www.stats.ox.ac.uk/pub/MASS4/

---

67. Basada en la función ppreg() de S-PLUS e implementado en R por B.D. Ripley, inicialmente para el paquete MASS.↩︎

68. No admite una fórmula del tipo respuesta ~ ., al intentar ejecutar npindexbw(O3 ~ ., data = train) se produciría un error. Para solventarlo tendríamos que escribir la expresión explícita de la fórmula, por ejemplo con la ayuda de reformulate(setdiff(colnames(train), "O3"), response = "O3"). Aparte de esto, el valor por defecto de nmulti = 5, número de reinicios con punto de partida aleatorio del algoritmo de optimización, puede producir que el tiempo de computación sea excesivo. Otro inconveniente es que los resultados de texto contienen caracteres inválidos para compilar en LaTeX y pueden aparecer errores al generar informes.↩︎