3.3 CART con el paquete rpart

La metodología CART está implementada en el paquete rpart (acrónimo de Recursive PARTitioning)³⁷, implementado por Therneau et al. (2013).

La función principal es rpart() y habitualmente se emplea de la forma:

rpart(formula, data, method, parms, control, ...)

• formula: permite especificar la respuesta y las variables predictoras de la forma habitual; se suele establecer de la forma respuesta ~ . para incluir todas las posibles variables explicativas.

• data: data.frame (opcional; donde se evaluará la fórmula) con la muestra de entrenamiento.

• method: método empleado para realizar las particiones, puede ser "anova" (regresión), "class" (clasificación), "poisson" (regresión de Poisson) o "exp" (supervivencia), o alternativamente una lista de funciones (con componentes init, split, eval; ver la vignette User Written Split Functions). Por defecto se selecciona a partir de la variable respuesta en formula, por ejemplo, si es un factor (lo recomendado en clasificación) emplea method = "class".

• parms: lista de parámetros opcionales para la partición en el caso de clasificación (o regresión de Poisson). Puede contener los componentes prior (vector de probabilidades previas; por defecto las frecuencias observadas), loss (matriz de pérdidas; con ceros en la diagonal y por defecto 1 en el resto) y split (criterio de error; por defecto "gini" o alternativamente "information").

• control: lista de opciones que controlan el algoritmo de partición, por defecto se seleccionan mediante la función rpart.control(), aunque también se pueden establecer en la llamada a la función principal, y los principales parámetros son:

  rpart.control(minsplit = 20, minbucket = round(minsplit/3), cp = 0.01, 
                xval = 10, maxdepth = 30, ...)

  • cp es el parámetro de complejidad \(\tilde \alpha\) para la poda del árbol, de forma que un valor de 1 se corresponde con un árbol sin divisiones, y un valor de 0, con un árbol de profundidad máxima. Adicionalmente, para reducir el tiempo de computación, el algoritmo empleado no realiza una partición si la proporción de reducción del error es inferior a este valor (valores más grandes simplifican el modelo y reducen el tiempo de computación).

  • maxdepth es la profundidad máxima del árbol (la profundidad de la raíz sería 0).

  • minsplit y minbucket son, respectivamente, los números mínimos de observaciones en un nodo intermedio para particionarlo y en un nodo terminal.

  • xval es el número de grupos (folds) para validación cruzada.

Para más detalles, consultar la documentación de esta función o la vignette Introduction to Rpart.

3.3.1 Ejemplo: regresión

Emplearemos el conjunto de datos winequality del paquete mpae, que contiene información fisico-química (fixed.acidity, volatile.acidity, citric.acid, residual.sugar, chlorides, free.sulfur.dioxide, total.sulfur.dioxide, density, pH, sulphates y alcohol) y sensorial (quality) de una muestra de 1250 vinos portugueses de la variedad vinho verde (Cortez et al., 2009)

library(mpae)
# data(winequality, package = "mpae")
str(winequality)

## 'data.frame':    1250 obs. of  12 variables:
##  $ fixed.acidity       : num  6.8 7.1 6.9 7.5 8.6 7.7 5.4 6.8 6.1 5.5 ...
##  $ volatile.acidity    : num  0.37 0.24 0.32 0.23 0.36 0.28 0.59 0.16 0.28 0.2..
##  $ citric.acid         : num  0.47 0.34 0.13 0.49 0.26 0.63 0.07 0.36 0.27 0.2..
##  $ residual.sugar      : num  11.2 1.2 7.8 7.7 11.1 11.1 7 1.3 4.7 1.6 ...
##  $ chlorides           : num  0.071 0.045 0.042 0.049 0.03 0.039 0.045 0.034 0..
##  $ free.sulfur.dioxide : num  44 6 11 61 43.5 58 36 32 56 23 ...
##  $ total.sulfur.dioxide: num  136 132 117 209 171 179 147 98 140 85 ...
##  $ density             : num  0.997 0.991 0.996 0.994 0.995 ...
##  $ pH                  : num  2.98 3.16 3.23 3.14 3.03 3.08 3.34 3.02 3.16 3.4..
##  $ sulphates           : num  0.88 0.46 0.37 0.3 0.49 0.44 0.57 0.58 0.42 0.42..
##  $ alcohol             : num  9.2 11.2 9.2 11.1 12 8.8 9.7 11.3 12.5 12.5 ...
##  $ quality             : int  5 4 5 7 5 4 6 6 8 5 ...

Como respuesta consideraremos la variable quality, mediana de al menos 3 evaluaciones de la calidad del vino realizadas por expertos, que los evaluaron entre 0 (muy malo) y 10 (excelente) como puede observarse en el gráfico de barras de la Figura 3.3.

barplot(table(winequality$quality), xlab = "Calidad", ylab = "Frecuencia")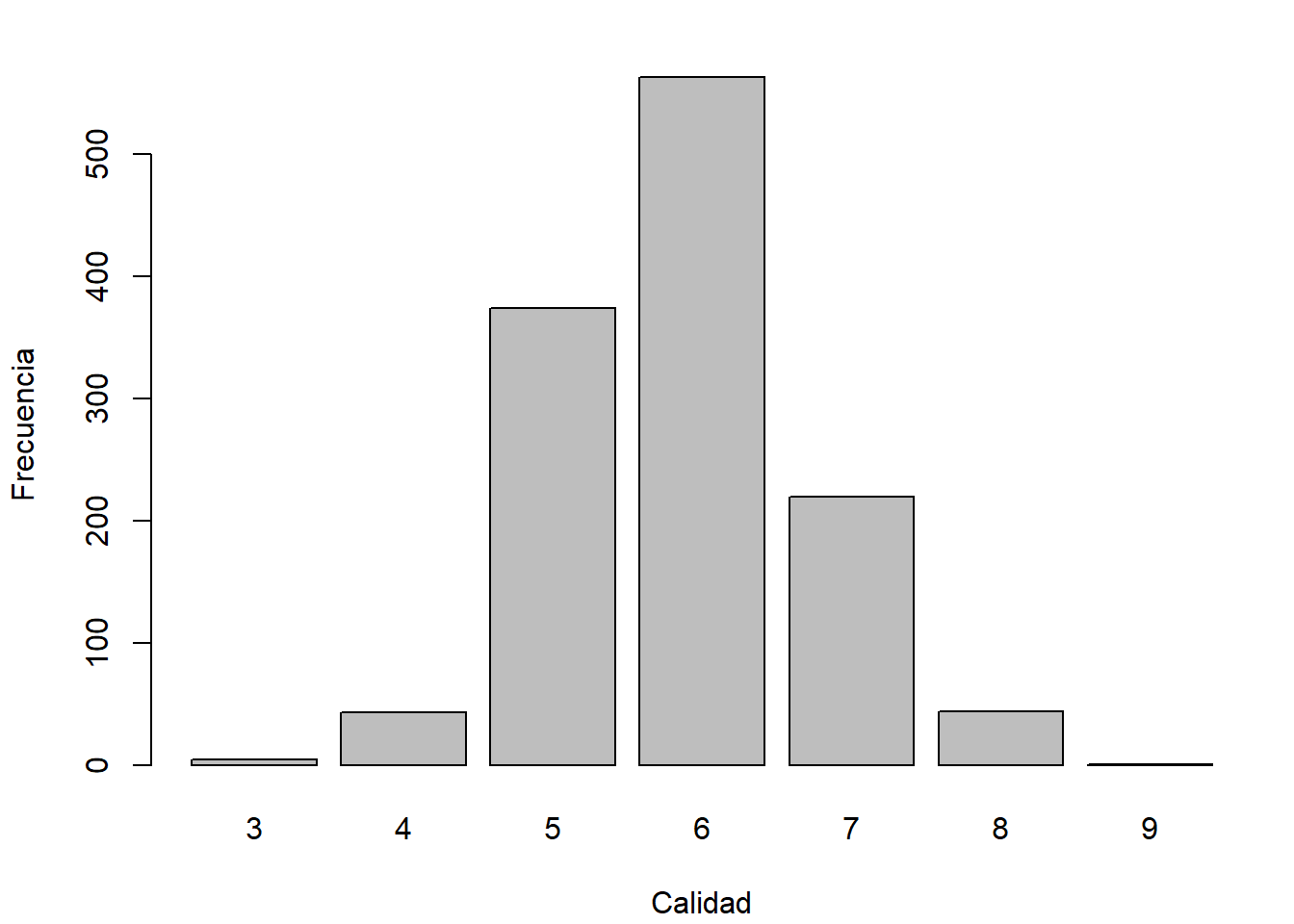

Figura 3.3: Distribución de las evaluaciones de la calidad del vino (winequality$quality).

En primer lugar se selecciona el 80 % de los datos como muestra de entrenamiento y el 20 % restante como muestra de test:

set.seed(1)
nobs <- nrow(winequality)
itrain <- sample(nobs, 0.8 * nobs)
train <- winequality[itrain, ]
test <- winequality[-itrain, ]

Podemos obtener el árbol de decisión con las opciones por defecto con el comando:

tree <- rpart(quality ~ ., data = train)

Al imprimirlo se muestra el número de observaciones e información sobre los distintos nodos (número de nodo, condición que define la partición, número de observaciones en el nodo, función de pérdida y predicción), marcando con un * los nodos terminales.

tree

## n= 1000 
## 
## node), split, n, deviance, yval
##       * denotes terminal node
## 
##  1) root 1000 768.960 5.8620  
##    2) alcohol< 10.75 622 340.810 5.5868  
##      4) volatile.acidity>=0.2575 329 154.760 5.3708  
##        8) total.sulfur.dioxide< 98.5 24  12.500 4.7500 *
##        9) total.sulfur.dioxide>=98.5 305 132.280 5.4197  
##         18) pH< 3.315 269 101.450 5.3532 *
##         19) pH>=3.315 36  20.750 5.9167 *
##      5) volatile.acidity< 0.2575 293 153.470 5.8294  
##       10) sulphates< 0.475 144  80.326 5.6597 *
##       11) sulphates>=0.475 149  64.993 5.9933 *
##    3) alcohol>=10.75 378 303.540 6.3148  
##      6) alcohol< 11.775 200 173.870 6.0750  
##       12) free.sulfur.dioxide< 11.5 15  10.933 4.9333 *
##       13) free.sulfur.dioxide>=11.5 185 141.810 6.1676  
##         26) volatile.acidity>=0.395 7  12.857 5.1429 *
##         27) volatile.acidity< 0.395 178 121.310 6.2079  
##           54) citric.acid>=0.385 31  21.935 5.7419 *
##           55) citric.acid< 0.385 147  91.224 6.3061 *
##      7) alcohol>=11.775 178 105.240 6.5843 *

Para representarlo se pueden emplear las herramientas del paquete rpart (ver Figura 3.4):

plot(tree)
text(tree)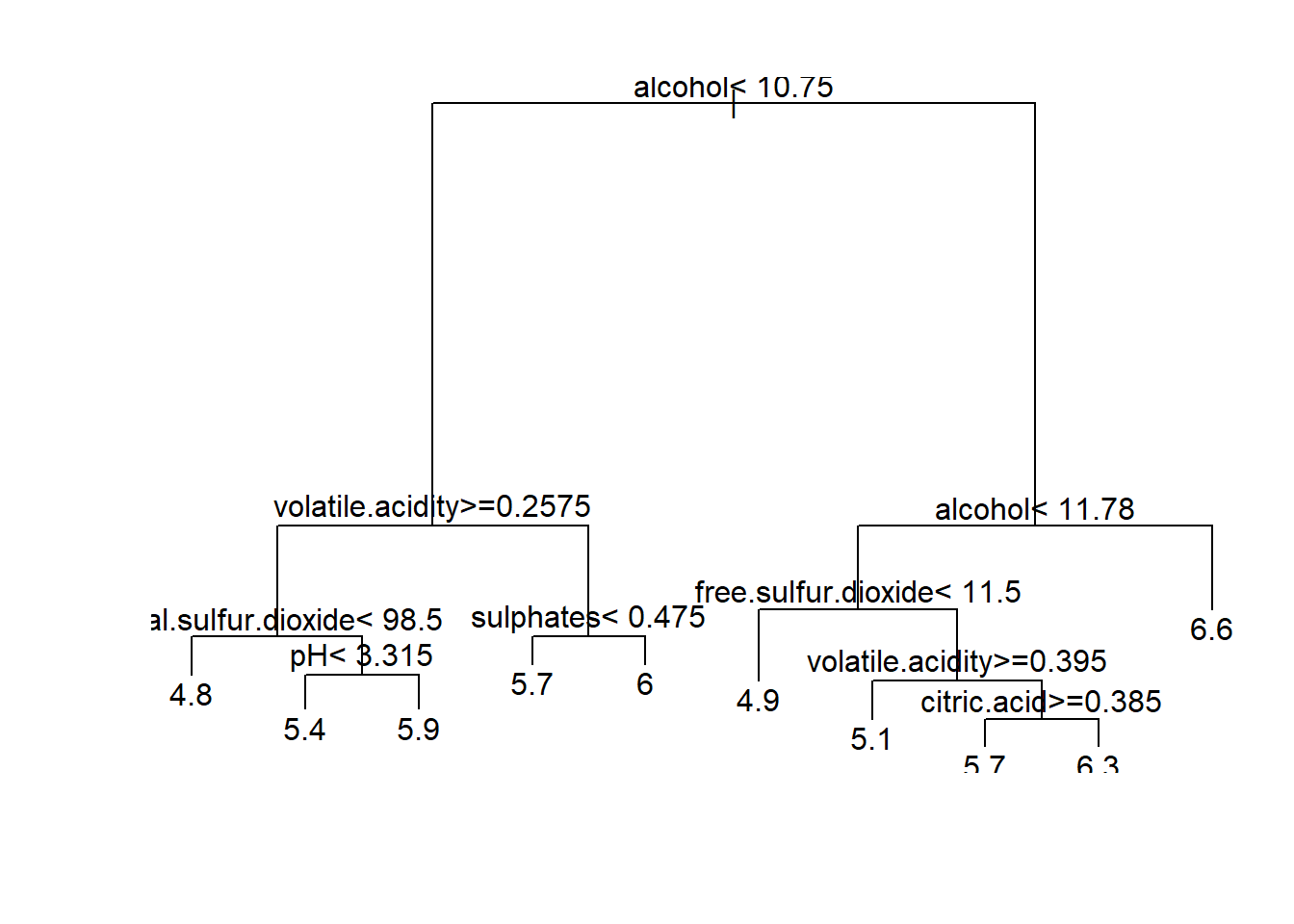

Figura 3.4: Árbol de regresión para predecir winequality$quality (obtenido con las opciones por defecto de rpart()).

Pero puede ser preferible emplear el paquete rpart.plot (Milborrow, 2019) (ver Figura 3.5):

library(rpart.plot)
rpart.plot(tree)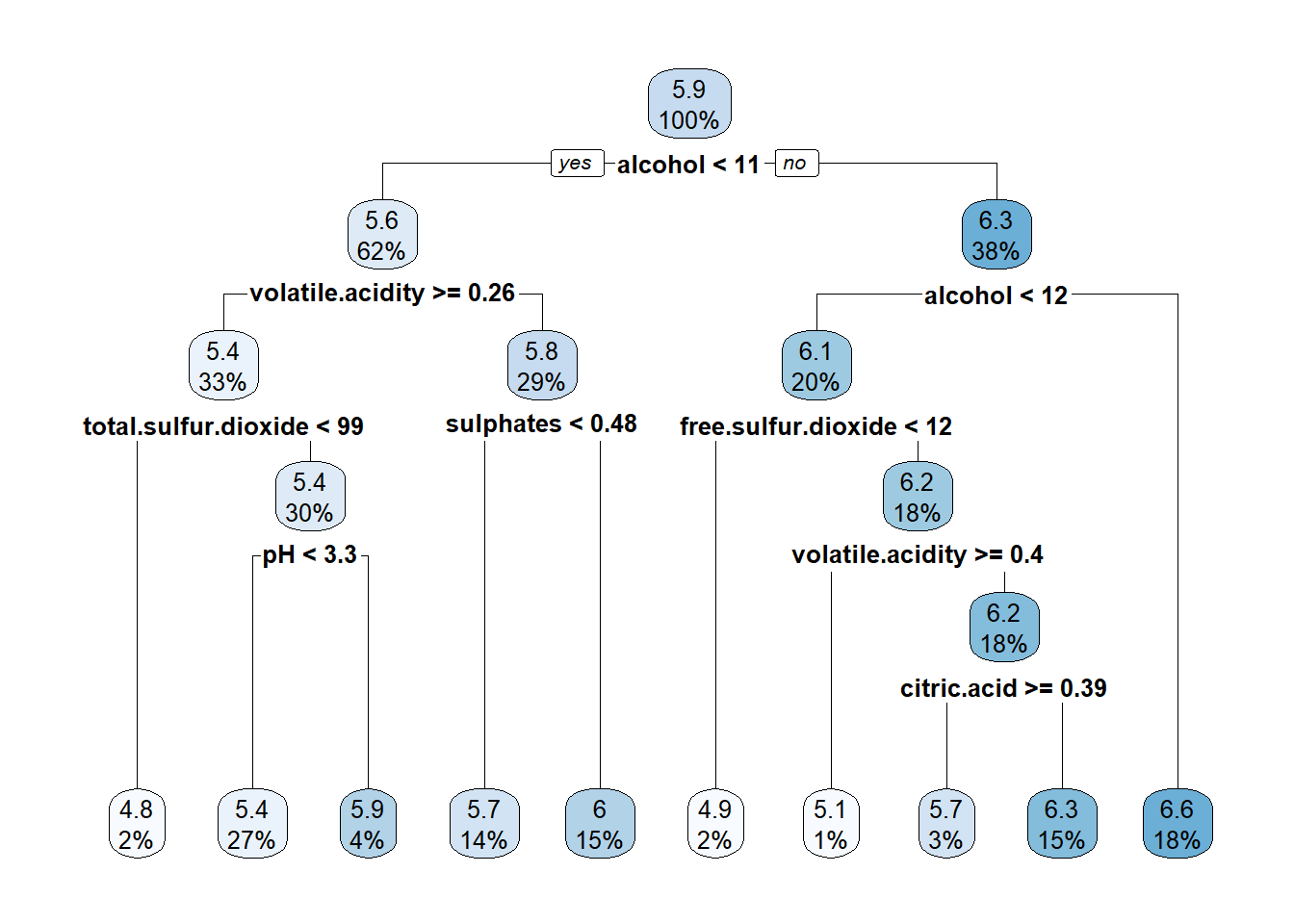  

Figura 3.5: Representación del árbol de regresión generada con rpart.plot().

Nos interesa conocer cómo se clasificaría a una nueva observación en los nodos terminales, junto con las predicciones correspondientes (la media de la respuesta en el nodo terminal). En los nodos intermedios, solo nos interesan las condiciones y el orden de las variables consideradas hasta llegar a las hojas. Para ello, puede ser útil imprimir las reglas:

rpart.rules(tree, style = "tall")

## quality is 4.8 when
##     alcohol < 11
##     volatile.acidity >= 0.26
##     total.sulfur.dioxide < 99
## 
## quality is 4.9 when
##     alcohol is 11 to 12
##     free.sulfur.dioxide < 12
## 
## quality is 5.1 when
##     alcohol is 11 to 12
##     volatile.acidity >= 0.40
##     free.sulfur.dioxide >= 12
## 
## quality is 5.4 when
##     alcohol < 11
##     volatile.acidity >= 0.26
##     total.sulfur.dioxide >= 99
##     pH < 3.3
## 
## quality is 5.7 when
##     alcohol < 11
##     volatile.acidity < 0.26
##     sulphates < 0.48
## 
## quality is 5.7 when
##     alcohol is 11 to 12
##     volatile.acidity < 0.40
##     free.sulfur.dioxide >= 12
##     citric.acid >= 0.39
## 
## quality is 5.9 when
##     alcohol < 11
##     volatile.acidity >= 0.26
##     total.sulfur.dioxide >= 99
##     pH >= 3.3
## 
## quality is 6.0 when
##     alcohol < 11
##     volatile.acidity < 0.26
##     sulphates >= 0.48
## 
## quality is 6.3 when
##     alcohol is 11 to 12
##     volatile.acidity < 0.40
##     free.sulfur.dioxide >= 12
##     citric.acid < 0.39
## 
## quality is 6.6 when
##     alcohol >= 12

Por defecto, el árbol se poda considerando cp = 0.01, que puede ser adecuado en muchas situaciones. Sin embargo, para seleccionar el valor óptimo de este hiperparámetro se puede emplear validación cruzada.

En primer lugar habría que establecer cp = 0 para construir el árbol completo, a la profundidad máxima. La profundidad máxima viene determinada por los valores de minsplit y minbucket, los cuales pueden ser ajustados manualmente dependiendo del número de observaciones o tratados como hiperparámetros; esto último no está implementado en rpart, ni en principio en caret³⁸.

tree <- rpart(quality ~ ., data = train, cp = 0)

Posteriormente, podemos emplear la función printcp() para obtener los valores de CP para los árboles (óptimos) de menor tamaño, junto con su error de validación cruzada xerror (reescalado de forma que el máximo de rel error es 1):

printcp(tree)

## 
## Regression tree:
## rpart(formula = quality ~ ., data = train, cp = 0)
## 
## Variables actually used in tree construction:
##  [1] alcohol              chlorides            citric.acid         
##  [4] density              fixed.acidity        free.sulfur.dioxide 
##  [7] pH                   residual.sugar       sulphates           
## [10] total.sulfur.dioxide volatile.acidity    
## 
## Root node error: 769/1000 = 0.769
## 
## n= 1000 
## 
##          CP nsplit rel error xerror   xstd
## 1  0.162047      0     1.000  1.002 0.0486
## 2  0.042375      1     0.838  0.858 0.0436
## 3  0.031765      2     0.796  0.828 0.0435
## 4  0.027487      3     0.764  0.813 0.0428
## 5  0.013044      4     0.736  0.770 0.0397
## 6  0.010596      6     0.710  0.782 0.0394
## 7  0.010266      7     0.700  0.782 0.0391
## 8  0.008408      9     0.679  0.782 0.0391
## 9  0.008139     10     0.671  0.801 0.0399
## 10 0.007806     11     0.663  0.800 0.0405
## 11 0.006842     13     0.647  0.798 0.0402
## 12 0.006738     15     0.633  0.814 0.0409
##  [ reached getOption("max.print") -- omitted 48 rows ]

También plotcp() para representarlos³⁹ (ver Figura 3.6):

plotcp(tree)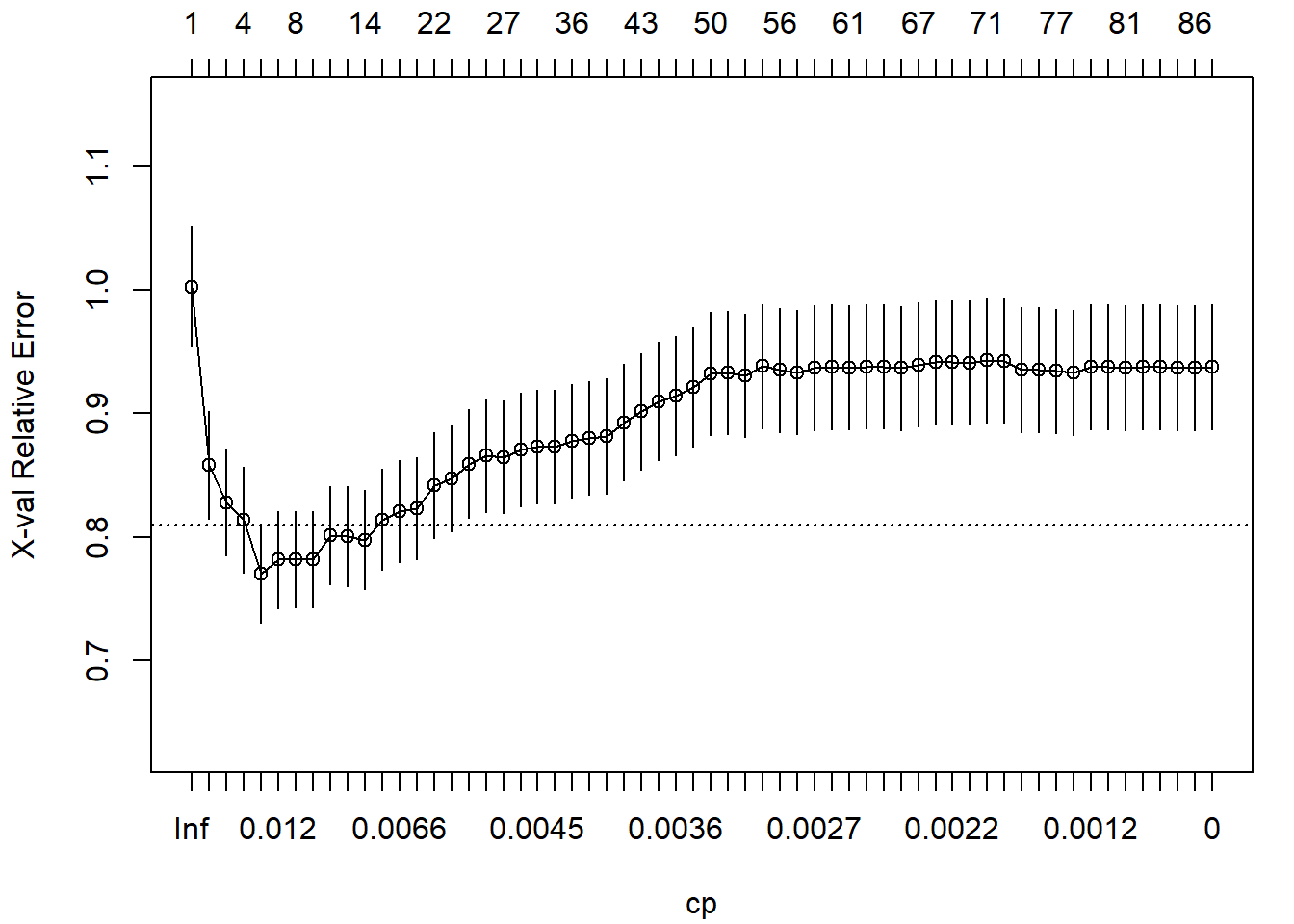

Figura 3.6: Error de validación cruzada (reescalado) dependiendo del parámetro de complejidad CP empleado en el ajuste del árbol de decisión.

La tabla con los valores de las podas (óptimas, dependiendo del parámetro de complejidad) está almacenada en la componente $cptable:

head(tree$cptable, 10)

##           CP nsplit rel error  xerror     xstd
## 1  0.1620471      0   1.00000 1.00203 0.048591
## 2  0.0423749      1   0.83795 0.85779 0.043646
## 3  0.0317653      2   0.79558 0.82810 0.043486
## 4  0.0274870      3   0.76381 0.81350 0.042814
## 5  0.0130437      4   0.73633 0.77038 0.039654
## 6  0.0105961      6   0.71024 0.78168 0.039353
## 7  0.0102661      7   0.69964 0.78177 0.039141
## 8  0.0084080      9   0.67911 0.78172 0.039123
## 9  0.0081392     10   0.67070 0.80117 0.039915
## 10 0.0078057     11   0.66256 0.80020 0.040481

A partir de esta misma tabla podríamos seleccionar el valor óptimo de forma automática, siguiendo el criterio de un error estándar de Breiman et al. (1984):

xerror <- tree$cptable[,"xerror"]
imin.xerror <- which.min(xerror)
# Valor óptimo
tree$cptable[imin.xerror, ]

##        CP    nsplit rel error    xerror      xstd 
##  0.013044  4.000000  0.736326  0.770380  0.039654

# Límite superior "oneSE rule" y complejidad mínima por debajo de ese valor
upper.xerror <- xerror[imin.xerror] + tree$cptable[imin.xerror, "xstd"]
icp <- min(which(xerror <= upper.xerror))
cp <- tree$cptable[icp, "CP"]

Para obtener el modelo final (ver Figura 3.7) podamos el árbol con el valor de complejidad obtenido 0.01304 (que en este caso coincide con el valor óptimo).

tree <- prune(tree, cp = cp)
rpart.plot(tree) 

Figura 3.7: Árbol de regresión resultante después de la poda (modelo final).

Podríamos estudiar el modelo final, por ejemplo, mediante el método summary.rpart(). Este método muestra, entre otras cosas, una medida (en porcentaje) de la importancia de las variables explicativas para la predicción de la respuesta (teniendo en cuenta todas las particiones, principales y secundarias, en las que se emplea cada variable explicativa). Como alternativa, podríamos emplear el siguiente código:

# summary(tree)
importance <- tree$variable.importance # Equivalente a caret::varImp(tree) 
importance <- round(100*importance/sum(importance), 1)
importance[importance >= 1]

##              alcohol              density            chlorides 
##                 36.1                 21.7                 11.3 
##     volatile.acidity total.sulfur.dioxide  free.sulfur.dioxide 
##                  8.7                  8.5                  5.0 
##       residual.sugar            sulphates          citric.acid 
##                  4.0                  1.9                  1.1 
##                   pH 
##                  1.1

El último paso sería evaluarlo en la muestra de test siguiendo los pasos descritos en la Sección 1.3.4. Representamos los valores observados frente a las predicciones (ver Figura 3.8):

obs <- test$quality
pred <- predict(tree, newdata = test)
# plot(pred, obs, xlab = "Predicción", ylab = "Observado")
plot(jitter(pred), jitter(obs), xlab = "Predicción", ylab = "Observado")
abline(a = 0, b = 1)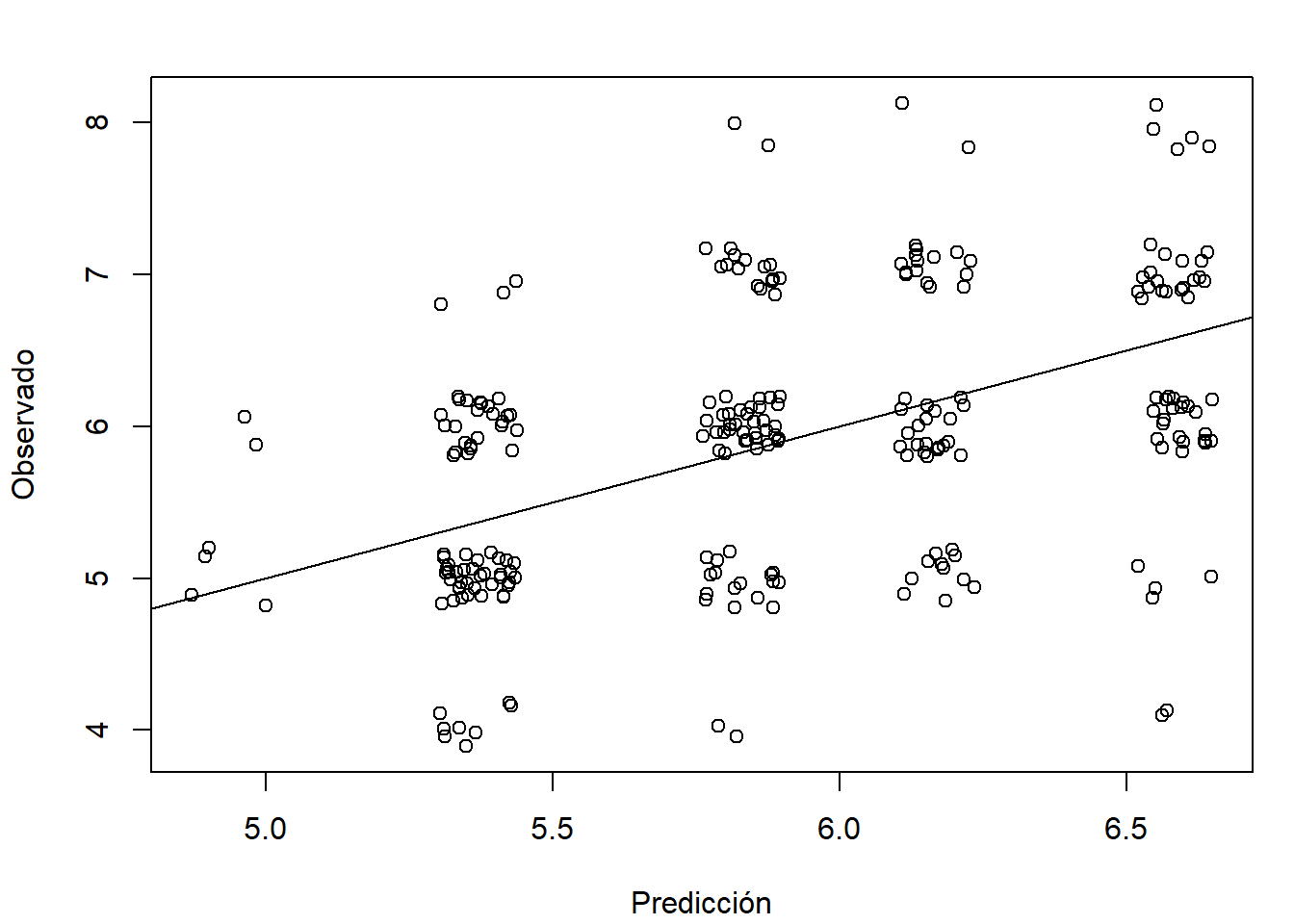

Figura 3.8: Gráfico de observaciones frente a predicciones (test$quality; se añade una perturbación para mostrar la distribución de los valores).

y calculamos medidas de error de las predicciones, bien empleando el paquete caret:

caret::postResample(pred, obs)

##     RMSE Rsquared      MAE 
##  0.81456  0.19695  0.65743

o con la función accuracy():

accuracy(pred, test$quality)

##         me       rmse        mae        mpe       mape  r.squared 
## -0.0012694  0.8145614  0.6574264 -1.9523422 11.5767160  0.1920077

Como se puede observar, el ajuste del modelo es bastante deficiente. Esto es habitual en árboles de regresión, especialmente si son tan pequeños, y por ello solo se utilizan, por lo general, en un análisis exploratorio inicial o como base para modelos más avanzados como los mostrados en el siguiente capítulo. En problemas de clasificación es más habitual que se puedan llegar a obtener buenos ajustes con árboles de decisión.

Ejercicio 3.1 Como se comentó en la introducción del Capítulo 1, al emplear el procedimiento habitual en AE de particionar los datos no se garantiza la reproducibilidad/repetibilidad de los resultados, ya que dependen de la semilla. El modelo ajustado puede variar con diferentes semillas, especialmente si el conjunto de entrenamiento es pequeño, aunque generalmente no se observan cambios significativos en las predicciones.

Podemos ilustrar el efecto de la semilla en los resultados empleando el ejemplo anterior. Para ello, repite el ajuste de un árbol de regresión considerando distintas semillas y compara los resultados obtenidos.

La dificultad podría estar en cómo comparar los resultados. Una posible solución sería mantener fija la muestra de test, de modo que no dependa de la semilla utilizada. Por comodidad, considera las primeras ntest observaciones del conjunto de datos como muestra de test. Posteriormente, para cada semilla, selecciona la muestra de entrenamiento de la forma habitual y ajusta un árbol. Finalmente, evalúa los resultados en la muestra de test.

Como base se puede utilizar el siguiente código:

ntest <- 10
test <- winequality[1:ntest, ]
df <- winequality[-(1:ntest), ]
nobs <- nrow(df)
# Para las distintas semillas
set.seed(semilla)
itrain <- sample(nobs, 0.8 * nobs)
train <- df[itrain, ]
# tree <- ...

Como observación final, en este caso el conjunto de datos no es muy grande y tampoco se obtuvo un buen ajuste con un árbol de regresión, por lo que sería de esperar que se observaran más diferencias.

Ejercicio 3.2 Como se indicó previamente, el paquete rpart implementa la selección del parámetro de complejidad mediante validación cruzada. Como alternativa, siguiendo la idea del Ejercicio 1.1, y considerando de nuevo el ejemplo anterior, particiona la muestra en datos de entrenamiento (70 %), de validación (15 %) y de test (15 %), para ajustar los árboles de decisión, seleccionar el parámetro de complejidad (el hiperparámetro) y evaluar las predicciones del modelo final, respectivamente.

Ejercicio 3.3 Una alternativa a particionar en entrenamiento y validación sería emplear bootstrap. La idea consiste en emplear una remuestra bootstrap del conjunto de datos de entrenamiento para ajustar el modelo y utilizar las observaciones no seleccionadas (se suelen denominar datos out-of-bag) como conjunto de validación.

set.seed(1)
nobs <- nrow(winequality)
itrain <- sample(nobs, 0.8 * nobs)
train <- winequality[itrain, ]
test <- winequality[-itrain, ]
# Indice muestra de entrenamiento bootstrap
set.seed(1)
ntrain <- nrow(train)
itrain.boot <- sample(ntrain, replace = TRUE)
train.boot <- train[itrain.boot, ]

La muestra bootstrap va a contener muchas observaciones repetidas y habrá observaciones no seleccionadas. La probabilidad de que una observación no sea seleccionada es \((1 - 1/n)^n \approx e^{-1} \approx 0.37\).

# Número de casos "out of bag"
ntrain - length(unique(itrain.boot))

## [1] 370

# Muestra "out of bag"
oob <- train[-itrain.boot, ]

El procedimiento restante sería análogo al caso anterior, cambiando train por train.boot y validate por oob. Sin embargo, lo recomendable sería repetir el proceso un número grande de veces y promediar los errores, especialmente cuando el tamaño muestral es pequeño (este enfoque se relaciona con el método de bagging, descrito en el siguiente capítulo). No obstante, y por simplicidad, realiza el ajuste empleando una única muestra bootstrap y evalúa las predicciones en la muestra de test.

3.3.2 Ejemplo: modelo de clasificación

Para ilustrar los árboles de clasificación CART, podemos emplear los datos anteriores de calidad de vino, considerando como respuesta una nueva variable taste que clasifica los vinos en “good” o “bad” dependiendo de si winequality$quality >= 6 (este conjunto de datos está disponible en mpae::winetaste).

# data(winetaste, package = "mpae")
winetaste <- winequality[, colnames(winequality)!="quality"]
winetaste$taste <- factor(winequality$quality < 6, 
                      labels = c('good', 'bad')) # levels = c('FALSE', 'TRUE')
str(winetaste)

## 'data.frame':    1250 obs. of  12 variables:
##  $ fixed.acidity       : num  6.8 7.1 6.9 7.5 8.6 7.7 5.4 6.8 6.1 5.5 ...
##  $ volatile.acidity    : num  0.37 0.24 0.32 0.23 0.36 0.28 0.59 0.16 0.28 0.2..
##  $ citric.acid         : num  0.47 0.34 0.13 0.49 0.26 0.63 0.07 0.36 0.27 0.2..
##  $ residual.sugar      : num  11.2 1.2 7.8 7.7 11.1 11.1 7 1.3 4.7 1.6 ...
##  $ chlorides           : num  0.071 0.045 0.042 0.049 0.03 0.039 0.045 0.034 0..
##  $ free.sulfur.dioxide : num  44 6 11 61 43.5 58 36 32 56 23 ...
##  $ total.sulfur.dioxide: num  136 132 117 209 171 179 147 98 140 85 ...
##  $ density             : num  0.997 0.991 0.996 0.994 0.995 ...
##  $ pH                  : num  2.98 3.16 3.23 3.14 3.03 3.08 3.34 3.02 3.16 3.4..
##  $ sulphates           : num  0.88 0.46 0.37 0.3 0.49 0.44 0.57 0.58 0.42 0.42..
##  $ alcohol             : num  9.2 11.2 9.2 11.1 12 8.8 9.7 11.3 12.5 12.5 ...
##  $ taste               : Factor w/ 2 levels "good","bad": 2 2 2 1 2 2 1 1 1 2 ..

table(winetaste$taste)

## 
## good  bad 
##  828  422

Como en el caso anterior, se contruyen las muestras de entrenamiento (80 %) y de test (20 %):

# set.seed(1)
# nobs <- nrow(winetaste)
# itrain <- sample(nobs, 0.8 * nobs)
train <- winetaste[itrain, ]
test <- winetaste[-itrain, ]

Al igual que en el caso anterior, podemos obtener el árbol de clasificación con las opciones por defecto (cp = 0.01 y split = "gini") con el comando:

tree <- rpart(taste ~ ., data = train)

Al imprimirlo, además de mostrar el número de nodo, la condición de la partición y el número de observaciones en el nodo, también se incluye el número de observaciones mal clasificadas, la predicción y las proporciones estimadas (frecuencias relativas en la muestra de entrenamiento) de las clases:

tree

## n= 1000 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 1000 338 good (0.66200 0.33800)  
##    2) alcohol>=10.117 541 100 good (0.81516 0.18484)  
##      4) free.sulfur.dioxide>=8.5 522  87 good (0.83333 0.16667)  
##        8) fixed.acidity< 8.55 500  73 good (0.85400 0.14600) *
##        9) fixed.acidity>=8.55 22   8 bad (0.36364 0.63636) *
##      5) free.sulfur.dioxide< 8.5 19   6 bad (0.31579 0.68421) *
##    3) alcohol< 10.117 459 221 bad (0.48148 0.51852)  
##      6) volatile.acidity< 0.2875 264 102 good (0.61364 0.38636)  
##       12) fixed.acidity< 7.45 213  71 good (0.66667 0.33333)  
##         24) citric.acid>=0.265 160  42 good (0.73750 0.26250) *
##         25) citric.acid< 0.265 53  24 bad (0.45283 0.54717)  
##           50) free.sulfur.dioxide< 42.5 33  13 good (0.60606 0.39394) *
##           51) free.sulfur.dioxide>=42.5 20   4 bad (0.20000 0.80000) *
##       13) fixed.acidity>=7.45 51  20 bad (0.39216 0.60784)  
##         26) total.sulfur.dioxide>=150 26  10 good (0.61538 0.38462) *
##         27) total.sulfur.dioxide< 150 25   4 bad (0.16000 0.84000) *
##      7) volatile.acidity>=0.2875 195  59 bad (0.30256 0.69744)  
##       14) pH>=3.235 49  24 bad (0.48980 0.51020)  
##         28) chlorides< 0.0465 18   4 good (0.77778 0.22222) *
##         29) chlorides>=0.0465 31  10 bad (0.32258 0.67742) *
##       15) pH< 3.235 146  35 bad (0.23973 0.76027) *

También puede ser preferible emplear el paquete rpart.plot para representarlo (ver Figura 3.9):

library(rpart.plot)
rpart.plot(tree) # Alternativa: rattle::fancyRpartPlot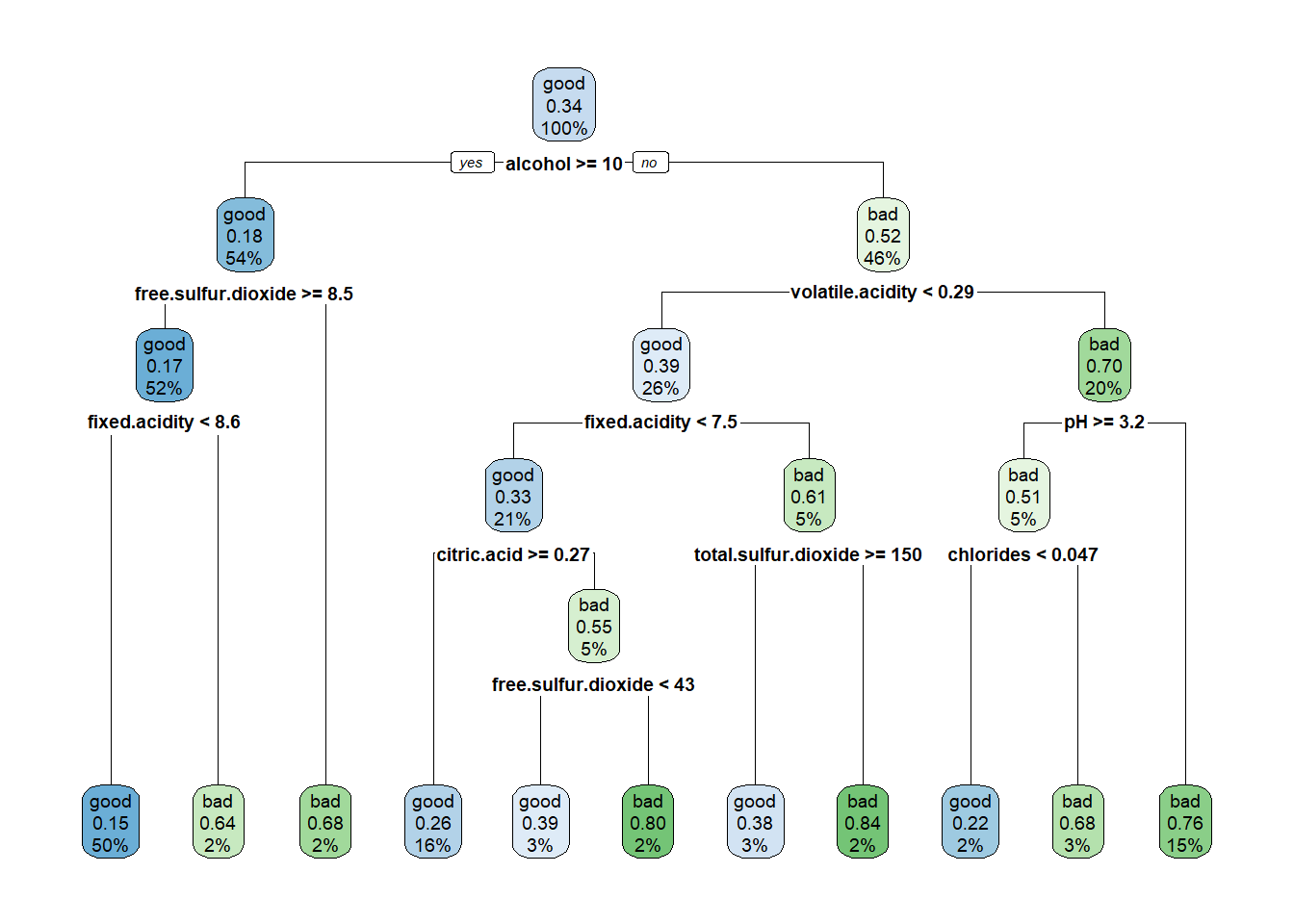

Figura 3.9: Árbol de clasificación de winetaste$taste (obtenido con las opciones por defecto).

Nos interesa cómo se clasificaría a una nueva observación, es decir, cómo se llegaría a los nodos terminales, así como su probabilidad estimada, que representa la frecuencia relativa de la clase más frecuente en el correspondiente nodo terminal. Para lograrlo, se puede modificar la información que se muestra en cada nodo (ver Figura 3.10):

rpart.plot(tree, 
           extra = 104,          # show fitted class, probs, percentages
           box.palette = "GnBu", # color scheme
           branch.lty = 3,       # dotted branch lines
           shadow.col = "gray",  # shadows under the node boxes
           nn = TRUE)            # display the node numbers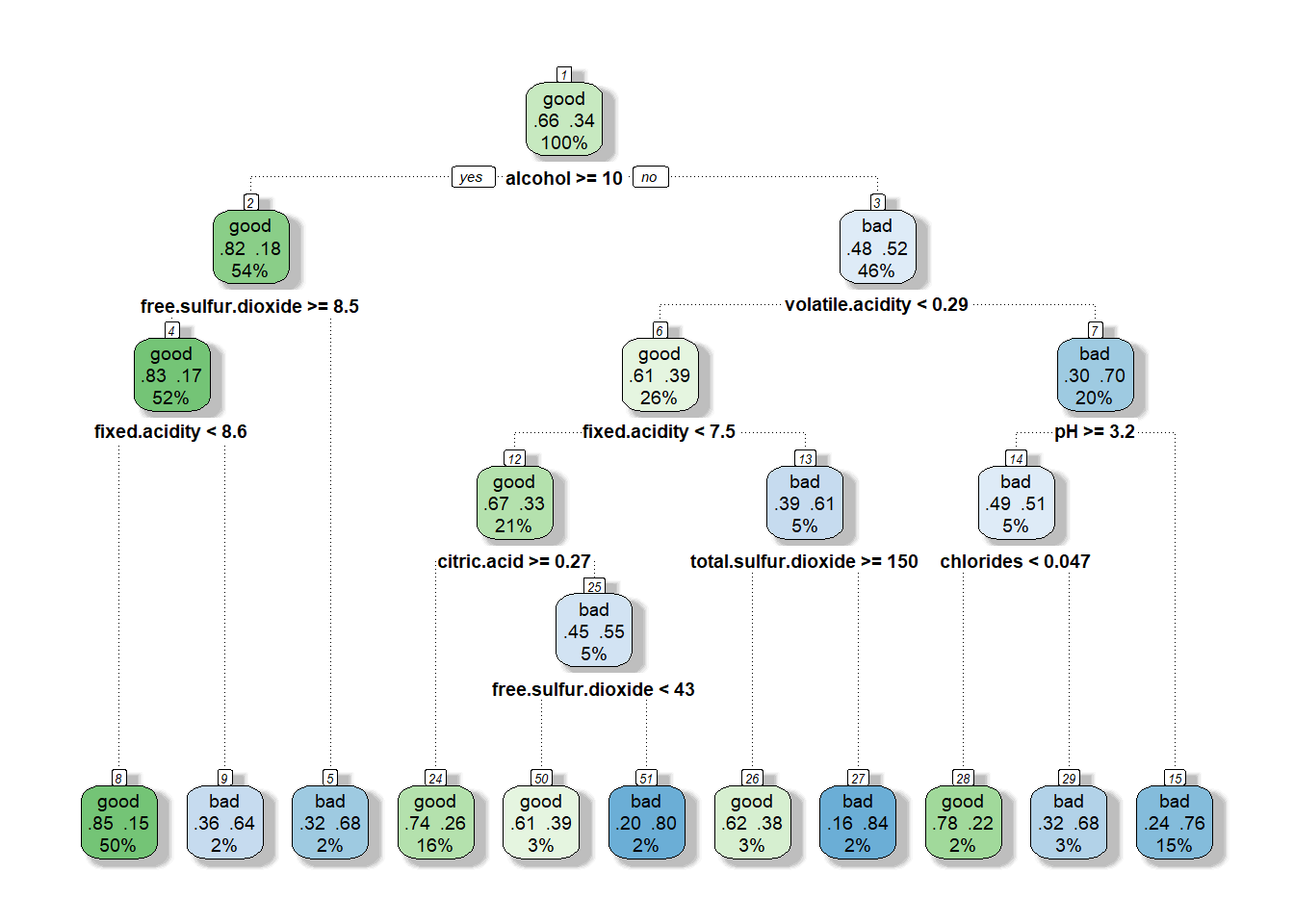 

Figura 3.10: Representación del árbol de clasificación de winetaste$taste con opciones adicionales.

Al igual que en el caso de regresión, puede ser de utilidad imprimir las reglas con rpart.rules(tree, style = "tall").

También se suele emplear el mismo procedimiento para seleccionar un valor óptimo para el hiperparámetro de complejidad: se construye un árbol de decisión completo y se emplea validación cruzada para podarlo. Además, si el número de observaciones es grande y las clases están más o menos balanceadas, se podría aumentar los valores mínimos de observaciones en los nodos intermedios y terminales⁴⁰, por ejemplo:

tree <- rpart(taste ~ ., data = train, cp = 0, minsplit = 30, minbucket = 10)

En este caso mantenemos el resto de valores por defecto:

tree <- rpart(taste ~ ., data = train, cp = 0)

Representamos los errores (reescalados) de validación cruzada (ver Figura 3.11):

plotcp(tree)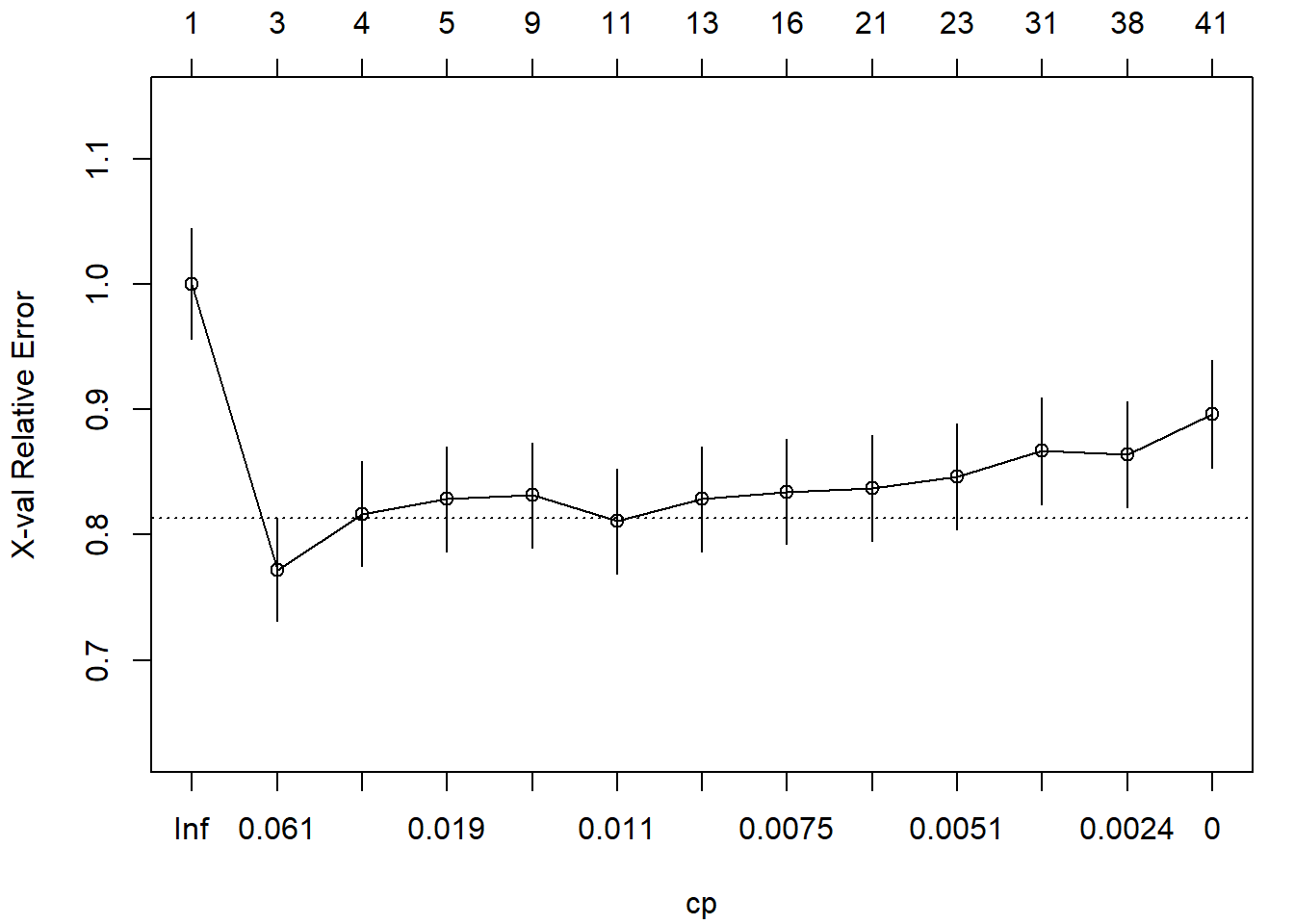

Figura 3.11: Evolución del error (reescalado) de validación cruzada en función del parámetro de complejidad.

Para obtener el modelo final, seleccionamos el valor óptimo de complejidad siguiendo el criterio de un error estándar de Breiman et al. (1984) y podamos el árbol (ver Figura 3.12).

xerror <- tree$cptable[,"xerror"]
imin.xerror <- which.min(xerror)
upper.xerror <- xerror[imin.xerror] + tree$cptable[imin.xerror, "xstd"]
icp <- min(which(xerror <= upper.xerror))
cp <- tree$cptable[icp, "CP"]
tree <- prune(tree, cp = cp)
rpart.plot(tree)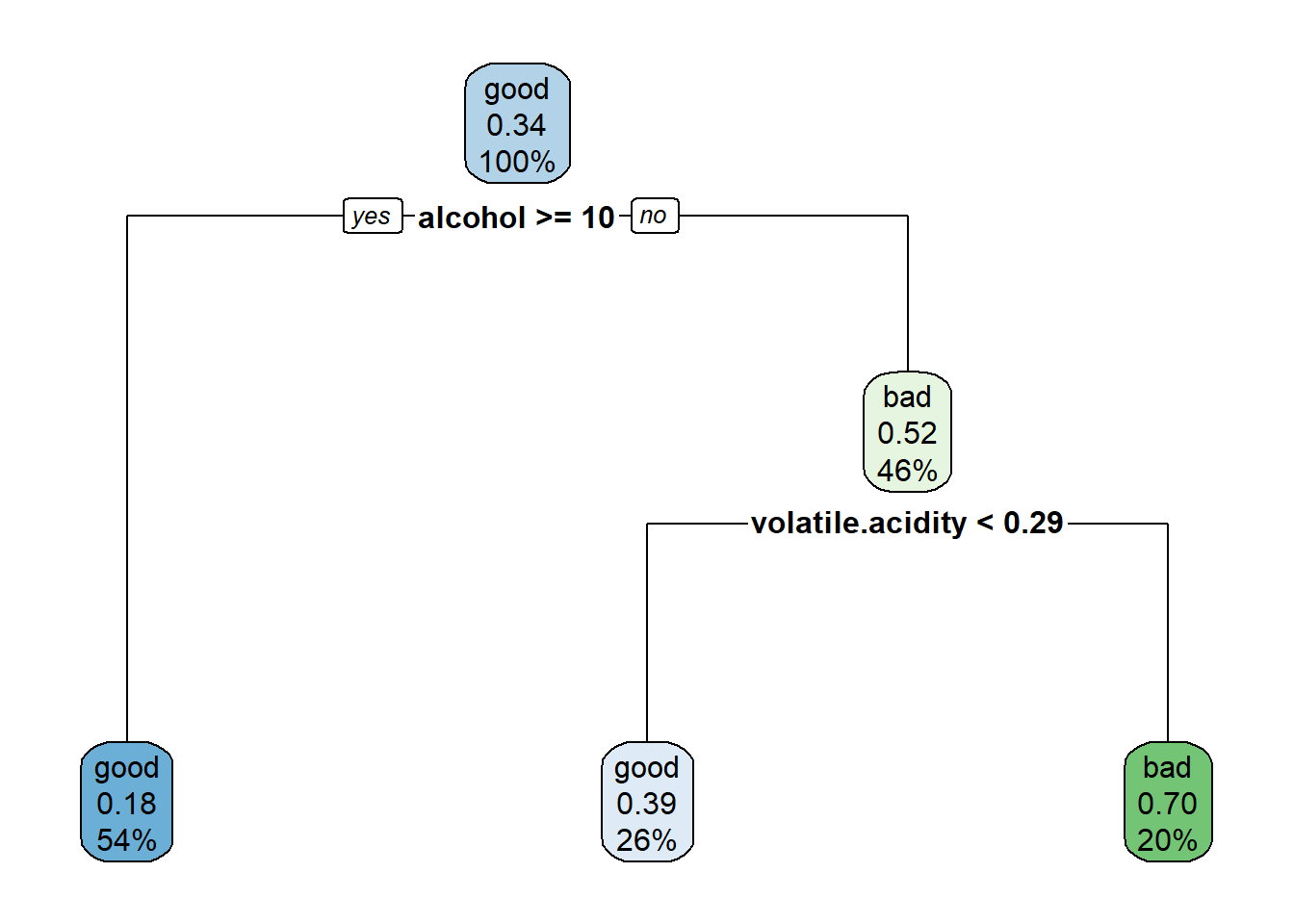 

Figura 3.12: Árbol de clasificación de winetaste$taste obtenido después de la poda (modelo final).

Si nos interesase estudiar la importancia de los predictores, podríamos utilizar el mismo código de la Sección 3.3.1 (no evaluado):

caret::varImp(tree)
importance <- tree$variable.importance
importance <- round(100*importance/sum(importance), 1)
importance[importance >= 1]

El último paso sería evaluar el modelo en la muestra de test siguiendo los pasos descritos en la Sección 1.3.5. El método predict.rpart() devuelve por defecto (type = "prob") una matriz con las probabilidades de cada clase, por lo que habría que establecer type = "class" para obtener la clase predicha (consultar la ayuda de esta función para más detalles).

obs <- test$taste
head(predict(tree, newdata = test))

##       good     bad
## 1  0.30256 0.69744
## 4  0.81516 0.18484
## 9  0.81516 0.18484
## 10 0.81516 0.18484
## 12 0.81516 0.18484
## 16 0.81516 0.18484

pred <- predict(tree, newdata = test, type = "class")
table(obs, pred)

##       pred
## obs    good bad
##   good  153  13
##   bad    54  30

caret::confusionMatrix(pred, obs)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction good bad
##       good  153  54
##       bad    13  30
##                                         
##                Accuracy : 0.732         
##                  95% CI : (0.673, 0.786)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 0.0125        
##                                         
##                   Kappa : 0.317         
##                                         
##  Mcnemar's Test P-Value : 1.02e-06      
##                                         
##             Sensitivity : 0.922         
##             Specificity : 0.357         
##          Pos Pred Value : 0.739         
##          Neg Pred Value : 0.698         
##              Prevalence : 0.664         
##          Detection Rate : 0.612         
##    Detection Prevalence : 0.828         
##       Balanced Accuracy : 0.639         
##                                         
##        'Positive' Class : good          
## 

Ejercicio 3.4 En este ejercicio se empleará el conjunto de datos mpae::bfan del paquete mpae utilizado anteriormente en las secciones 2.2 y 2.3. Considerando como respuesta la variable indicadora bfan, que clasifica a los individuos en Yes o No dependiendo de si su porcentaje de grasa corporal es superior al rango normal:

1. Particiona los datos, considerando un 80 % de las observaciones como muestra de aprendizaje y el 20 % restante como muestra de test.

2. Ajusta un árbol de decisión a los datos de entrenamiento seleccionando el parámetro de complejidad mediante la regla de un error estándar de Breiman.

3. Representa e interpreta el árbol resultante, estudiando la importancia de las variables predictoras.

4. Evalúa la precisión de las predicciones en la muestra de test (precisión, sensibilidad y especificidad) y la estimación de las probabilidades mediante el AUC.

3.3.3 Interfaz de caret

En caret podemos ajustar un árbol CART seleccionando method = "rpart". Por defecto, caret realiza bootstrap de las observaciones para seleccionar el valor óptimo del hiperparámetro cp (considerando únicamente tres posibles valores). Si queremos emplear validación cruzada, como se hizo en el caso anterior, podemos emplear la función auxiliar trainControl(), y para considerar un mayor rango de posibles valores podemos hacer uso del argumento tuneLength (ver Figura 3.13).

library(caret)
# modelLookup("rpart")  # Información sobre hiperparámetros
set.seed(1)
trControl <- trainControl(method = "cv", number = 10)
caret.rpart <- train(taste ~ ., method = "rpart", data = train, 
                     tuneLength = 20, trControl = trControl) 
caret.rpart

## CART 
## 
## 1000 samples
##   11 predictor
##    2 classes: 'good', 'bad' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 901, 900, 900, 900, 900, 900, ... 
## Resampling results across tuning parameters:
## 
##   cp        Accuracy  Kappa  
##   0.000000  0.70188   0.34873
##   0.005995  0.73304   0.38706
##   0.011990  0.74107   0.38785
##   0.017985  0.72307   0.33745
##   0.023980  0.73607   0.36987
##   0.029975  0.73407   0.35064
##   0.035970  0.73207   0.34182
##   0.041965  0.73508   0.34227
##   0.047960  0.73508   0.34227
##   0.053955  0.73508   0.34227
##   0.059950  0.73508   0.34227
##   0.065945  0.73508   0.34227
##   0.071940  0.73508   0.34227
##   0.077935  0.73508   0.34227
##   0.083930  0.73508   0.34227
##   0.089925  0.73508   0.34227
##   0.095920  0.73508   0.34227
##   0.101915  0.73508   0.34227
##   0.107910  0.72296   0.29433
##   0.113905  0.68096   0.10877
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was cp = 0.01199.

ggplot(caret.rpart, highlight = TRUE)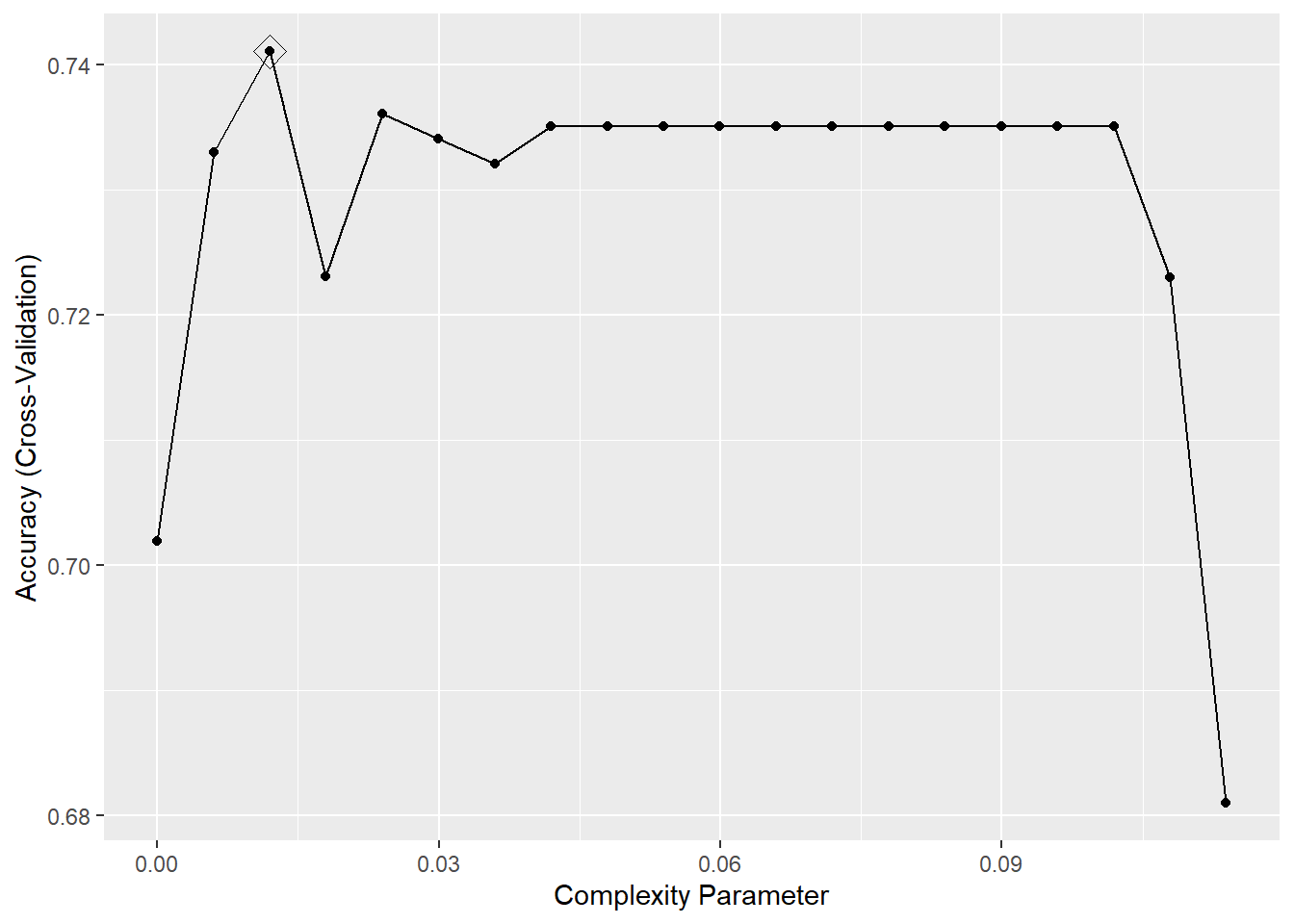

Figura 3.13: Evolución de la precisión (obtenida mediante validación cruzada) dependiendo del parámetro de complejidad, resaltando el valor óptimo.

El modelo final se devuelve en la componente $finalModel (ver Figura 3.14):

caret.rpart$finalModel

## n= 1000 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 1000 338 good (0.66200 0.33800)  
##    2) alcohol>=10.117 541 100 good (0.81516 0.18484)  
##      4) free.sulfur.dioxide>=8.5 522  87 good (0.83333 0.16667)  
##        8) fixed.acidity< 8.55 500  73 good (0.85400 0.14600) *
##        9) fixed.acidity>=8.55 22   8 bad (0.36364 0.63636) *
##      5) free.sulfur.dioxide< 8.5 19   6 bad (0.31579 0.68421) *
##    3) alcohol< 10.117 459 221 bad (0.48148 0.51852)  
##      6) volatile.acidity< 0.2875 264 102 good (0.61364 0.38636)  
##       12) fixed.acidity< 7.45 213  71 good (0.66667 0.33333)  
##         24) citric.acid>=0.265 160  42 good (0.73750 0.26250) *
##         25) citric.acid< 0.265 53  24 bad (0.45283 0.54717)  
##           50) free.sulfur.dioxide< 42.5 33  13 good (0.60606 0.39394) *
##           51) free.sulfur.dioxide>=42.5 20   4 bad (0.20000 0.80000) *
##       13) fixed.acidity>=7.45 51  20 bad (0.39216 0.60784)  
##         26) total.sulfur.dioxide>=150 26  10 good (0.61538 0.38462) *
##         27) total.sulfur.dioxide< 150 25   4 bad (0.16000 0.84000) *
##      7) volatile.acidity>=0.2875 195  59 bad (0.30256 0.69744)  
##       14) pH>=3.235 49  24 bad (0.48980 0.51020)  
##         28) chlorides< 0.0465 18   4 good (0.77778 0.22222) *
##         29) chlorides>=0.0465 31  10 bad (0.32258 0.67742) *
##       15) pH< 3.235 146  35 bad (0.23973 0.76027) *

rpart.plot(caret.rpart$finalModel)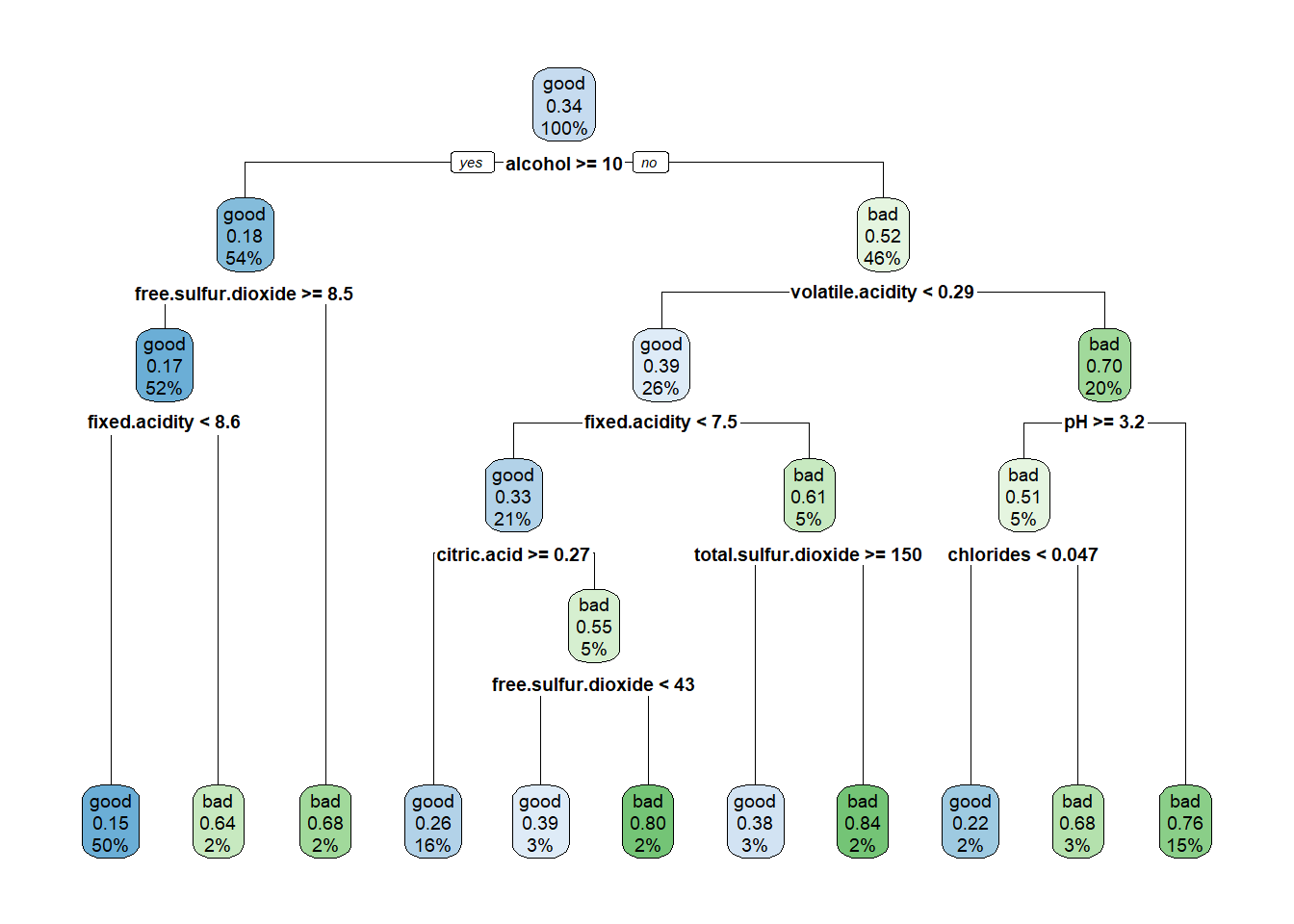

Figura 3.14: Árbol de clasificación de winetaste$taste, obtenido con la complejidad “óptima” (empleando caret).

Para utilizar la regla de “un error estándar” se puede añadir selectionFunction = "oneSE" en las opciones de entrenamiento⁴¹:

set.seed(1)
trControl <- trainControl(method = "cv", number = 10, 
                          selectionFunction = "oneSE")
caret.rpart <- train(taste ~ ., method = "rpart", data = train, 
                     tuneLength = 20, trControl = trControl) 
# ggplot(caret.rpart, highlight = TRUE)
caret.rpart

## CART 
## 
## 1000 samples
##   11 predictor
##    2 classes: 'good', 'bad' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 901, 900, 900, 900, 900, 900, ... 
## Resampling results across tuning parameters:
## 
##   cp        Accuracy  Kappa  
##   0.000000  0.70188   0.34873
##   0.005995  0.73304   0.38706
##   0.011990  0.74107   0.38785
##   0.017985  0.72307   0.33745
##   0.023980  0.73607   0.36987
##   0.029975  0.73407   0.35064
##   0.035970  0.73207   0.34182
##   0.041965  0.73508   0.34227
##   0.047960  0.73508   0.34227
##   0.053955  0.73508   0.34227
##   0.059950  0.73508   0.34227
##   0.065945  0.73508   0.34227
##   0.071940  0.73508   0.34227
##   0.077935  0.73508   0.34227
##   0.083930  0.73508   0.34227
##   0.089925  0.73508   0.34227
##   0.095920  0.73508   0.34227
##   0.101915  0.73508   0.34227
##   0.107910  0.72296   0.29433
##   0.113905  0.68096   0.10877
## 
## Accuracy was used to select the optimal model using  the one SE rule.
## The final value used for the model was cp = 0.10192.

Como cabría esperar, el modelo resultante es más simple (ver Figura 3.15):

rpart.plot(caret.rpart$finalModel)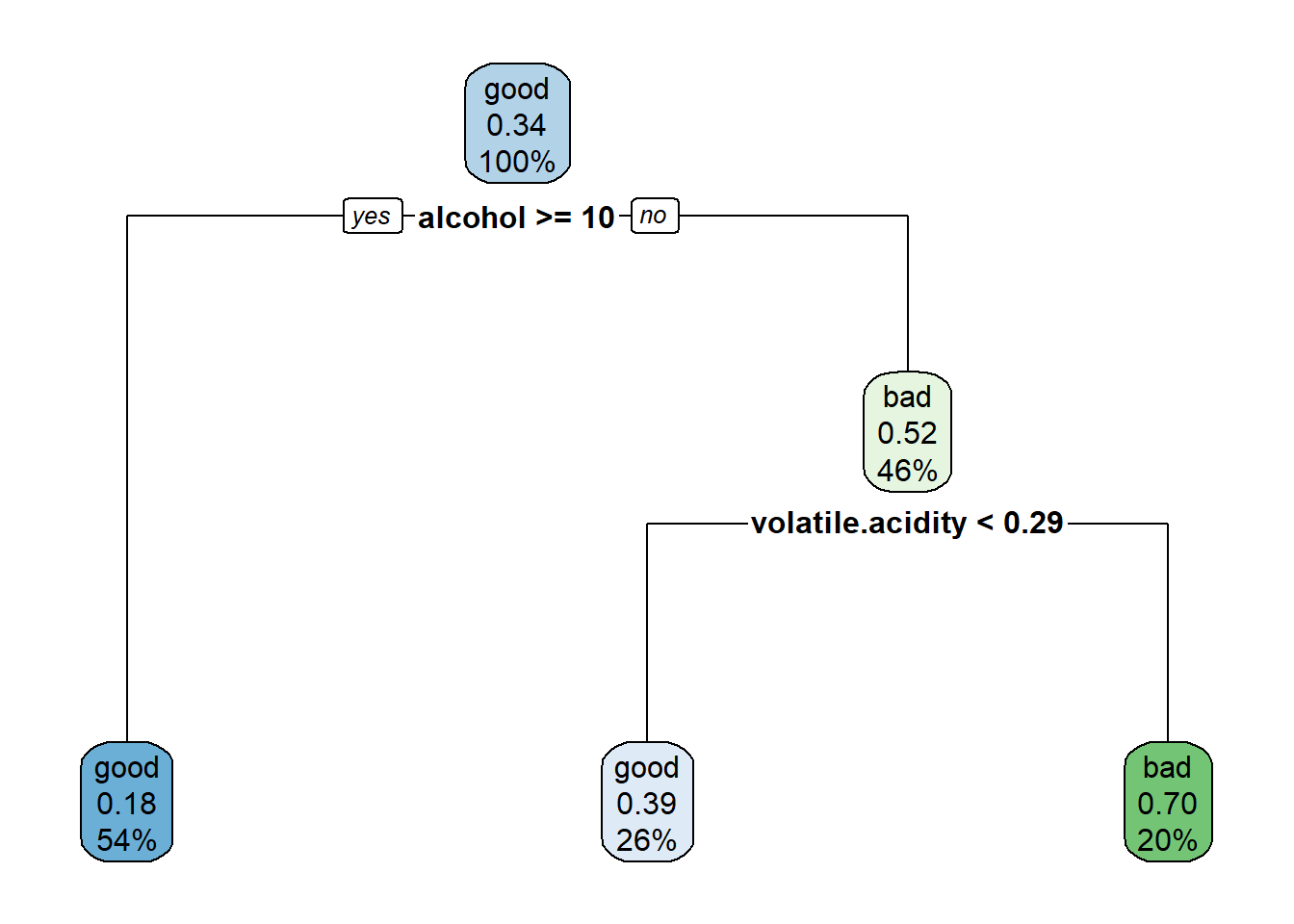

Figura 3.15: Árbol de clasificación de winetaste$taste, obtenido con la regla de un error estándar para seleccionar la complejidad (empleando caret).

Adicionalmente, representamos la importancia de los predictores (ver Figura 3.16):

var.imp <- varImp(caret.rpart)
plot(var.imp)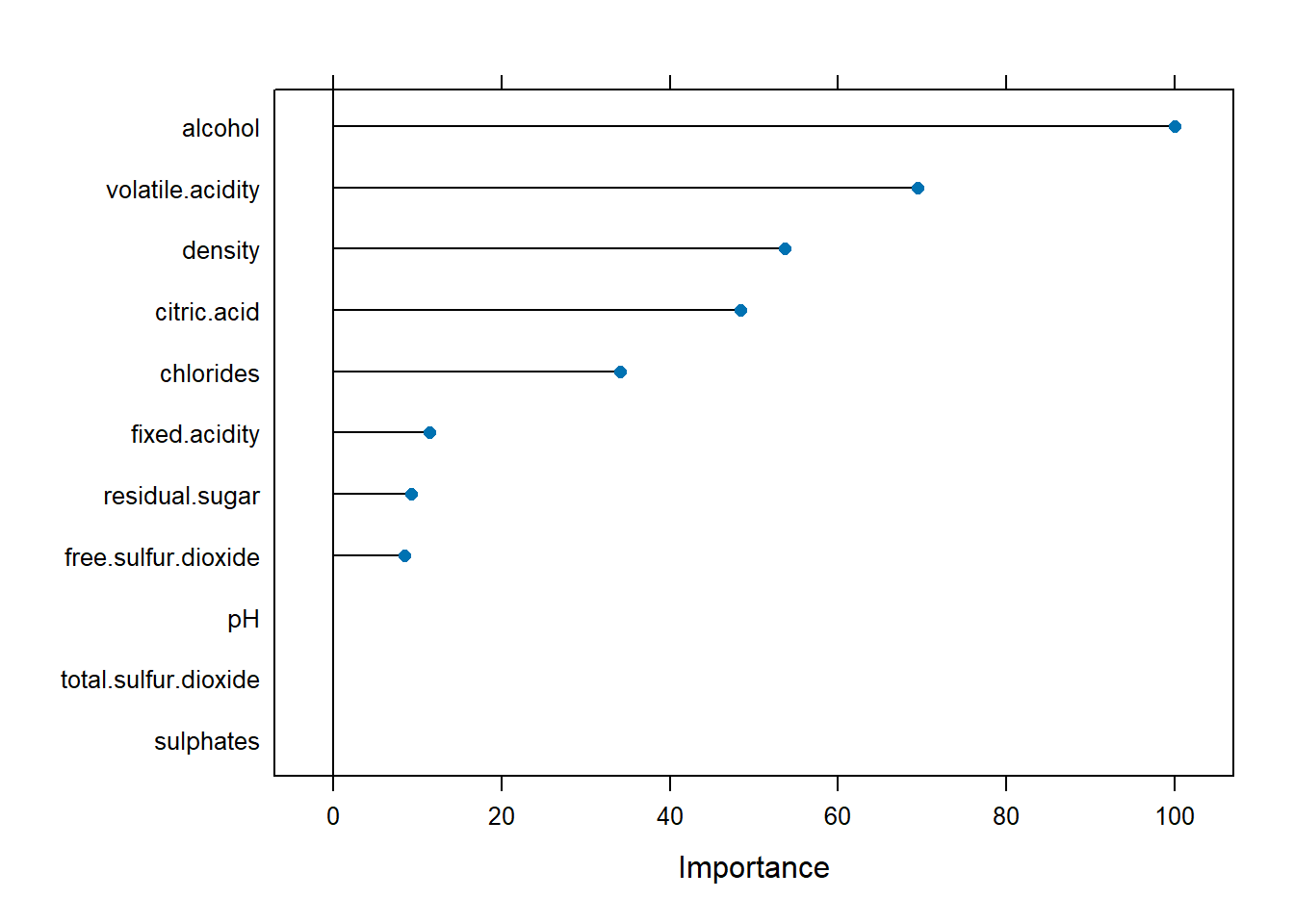

Figura 3.16: Importancia de los (posibles) predictores según el modelo obtenido con la regla de un error estándar.

Finalmente, calculamos las predicciones con el método predict.train() y posteriormente evaluamos su precisión con confusionMatrix():

pred <- predict(caret.rpart, newdata = test)
confusionMatrix(pred, test$taste)

## Confusion Matrix and Statistics
## 
##           Reference
## Prediction good bad
##       good  153  54
##       bad    13  30
##                                         
##                Accuracy : 0.732         
##                  95% CI : (0.673, 0.786)
##     No Information Rate : 0.664         
##     P-Value [Acc > NIR] : 0.0125        
##                                         
##                   Kappa : 0.317         
##                                         
##  Mcnemar's Test P-Value : 1.02e-06      
##                                         
##             Sensitivity : 0.922         
##             Specificity : 0.357         
##          Pos Pred Value : 0.739         
##          Neg Pred Value : 0.698         
##              Prevalence : 0.664         
##          Detection Rate : 0.612         
##    Detection Prevalence : 0.828         
##       Balanced Accuracy : 0.639         
##                                         
##        'Positive' Class : good          
## 

También podríamos calcular las estimaciones de las probabilidades (añadiendo el argumento type = "prob") y, por ejemplo, generar la curva ROC con pROC::roc() (ver Figura 3.17):

library(pROC)
p.est <- predict(caret.rpart, newdata = test, type = "prob")
roc_tree <- roc(response = obs, predictor = p.est$good)
roc_tree

## 
## Call:
## roc.default(response = obs, predictor = p.est$good)
## 
## Data: p.est$good in 166 controls (obs good) > 84 cases (obs bad).
## Area under the curve: 0.72

plot(roc_tree, xlab = "Especificidad", ylab = "Sensibilidad")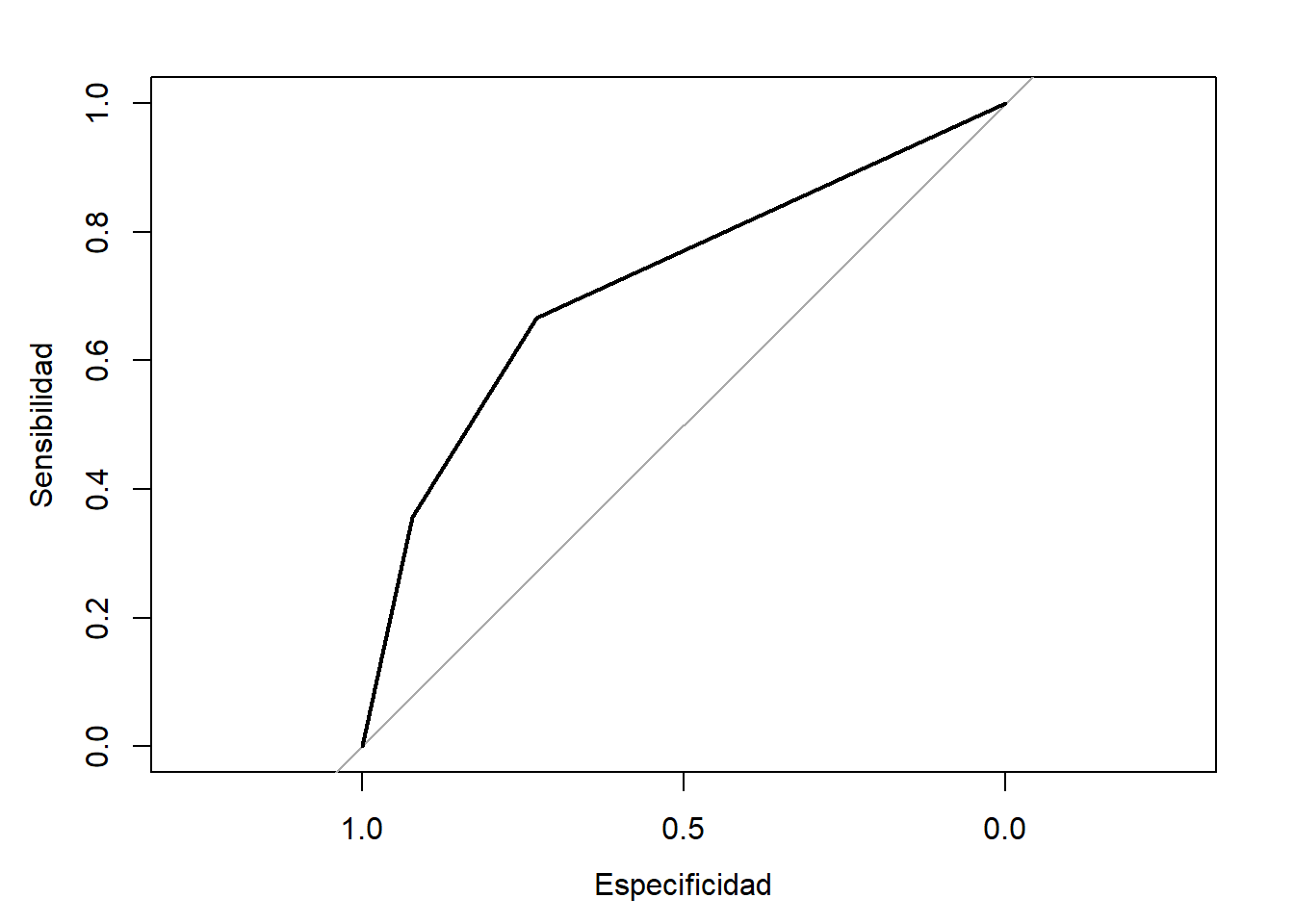

Figura 3.17: Curva ROC correspondiente al árbol de clasificación de winetaste$taste.

A la vista de los resultados, los árboles de clasificación no parecen muy adecuados para este problema. Sobre todo por la mala clasificación en la categoría "bad" (en este último ajuste se obtuvo un valor de especificidad de 0.3571 en la muestra de test), lo que podría ser debido a que las clases están desbalanceadas y en el ajuste recibe mayor peso el error en la clase mayoritaria. Para tratar de evitarlo, se podría emplear una matriz de pérdidas a través del componente loss del argumento parms (en el Ejercicio 5.1 se propone una aproximación similar). También se podría pensar en cambiar el criterio de optimalidad. Por ejemplo, emplear el coeficiente kappa en lugar de la precisión (solo habría que establecer metric = "Kappa" en la llamada a la función train()), o el área bajo la curva ROC (ver Ejercicio 5.3).

Ejercicio 3.5 Continuando con el Ejercicio 3.4, emplea caret para clasificar los individuos mediante un árbol de decisión. Utiliza la misma partición de los datos, seleccionando el parámetro de complejidad mediante validación cruzada con 10 grupos y el criterio de un error estándar de Breiman. Representa e interpreta el árbol resultante (comentando la importancia de las variables) y evalúa la precisión de las predicciones en la muestra de test.

Bibliografía

Breiman, L., Friedman, J., Stone, C. J., y Olshen, R. A. (1984). Classification and Regression Trees. Taylor; Francis.

Cortez, P., Cerdeira, A., Almeida, F., Matos, T., y Reis, J. (2009). Modeling wine preferences by data mining from physicochemical properties. Decision Support Systems, 47(4), 547-553. https://doi.org/10.1016/j.dss.2009.05.016

Milborrow, S. (2019). rpart.plot: Plot ’rpart’ Models: An Enhanced Version of ’plot.rpart’. http://cran.r-project.org/package=rpart.plot/

Therneau, T. M., Atkinson, E. J., y Ripley, B. (2013). Rpart: Recursive Partitioning and Regression Trees. http://cran.r-project.org/package=rpart/

---

37. El paquete tree es una traducción del original en S.↩︎

38. Los parámetros maxsurrogate, usesurrogate y surrogatestyle serían de utilidad si hay datos faltantes.↩︎

39. Realmente en la tabla de texto se muestra el valor mínimo de CP, ya que se obtendría la misma solución para un rango de valores de CP (desde ese valor hasta el anterior, sin incluirlo), mientras que en el gráfico generado por plotcp() se representa la media geométrica de los extremos de ese intervalo.↩︎

40. Otra opción, más interesante para regresión, sería considerar estos valores como hiperparámetros.↩︎

41. En principio también se podría utilizar la regla de un error estándar estableciendo method = "rpart1SE" en la llamada a train(), pero caret implementa internamente este método y en ocasiones no se obtienen los resultados esperados.↩︎