5.3 Máquinas de soporte vectorial
De manera similar a lo discutido en el Capítulo 3, dedicado a árboles, donde se comentó que estos serán efectivos en la medida en la que los datos se separen adecuadamente utilizando particiones basadas en rectángulos, los dos métodos de clasificación que hemos visto hasta ahora en este capítulo serán efectivos si hay una frontera lineal que separe los datos de las dos categorías. En caso contrario, un clasificador de soporte vectorial podría ser inadecuado. Una solución natural es sustituir el hiperplano, lineal en esencia, por otra función que dependa de las variables predictoras \(X_1,X_2, \ldots, X_n\), utilizando por ejemplo una expresión polinómica o incluso una expresión no aditiva en los predictores. Pero esta solución puede resultar computacionalmente compleja.
En Boser et al. (1992) se propuso sustituir, en todos los cálculos que conducen a la expresión \[m(\mathbf{x}) = \beta_0 + \sum_{i\in S} \alpha_i \mathbf{x}^t \mathbf{x}_i\] los productos escalares \(\mathbf{x}^t \mathbf{x}_i\), \(\mathbf{x}_i^t \mathbf{x}_j\) por funciones alternativas de los datos que reciben el nombre de funciones kernel, obteniendo la máquina de soporte vectorial \[m(\mathbf{x}) = \beta_0 + \sum_{i\in S} \alpha_i K(\mathbf{x}, \mathbf{x}_i)\]
Algunas de las funciones kernel más utilizadas son:
Kernel lineal
\[K(\mathbf{x}, \mathbf{y}) = \mathbf{x}^t \mathbf{y}\]
Kernel polinómico
\[K(\mathbf{x}, \mathbf{y}) = (1 + \gamma \mathbf{x}^t \mathbf{y})^d\]
Kernel radial
\[K(\mathbf{x}, \mathbf{y}) = \mbox{exp} (-\gamma \| \mathbf{x} - \mathbf{y} \|^2)\]
Tangente hiperbólica
\[K(\mathbf{x}, \mathbf{y}) = \mbox{tanh} (1 + \gamma \mathbf{x}^t \mathbf{y})\]
Antes de construir el modelo, es recomendable centrar y reescalar los datos para evitar que los valores grandes ahoguen al resto de los datos. Por supuesto, tiene que hacerse la misma transformación a todos los datos, incluidos los datos de test. La posibilidad de utilizar distintos kernels da mucha flexibilidad a esta metodología, pero es muy importante seleccionar adecuadamente los parámetros de la función kernel (\(\gamma,d\)) y el parámetro \(C\) para evitar sobreajustes, como se ilustra en la Figura 5.3.
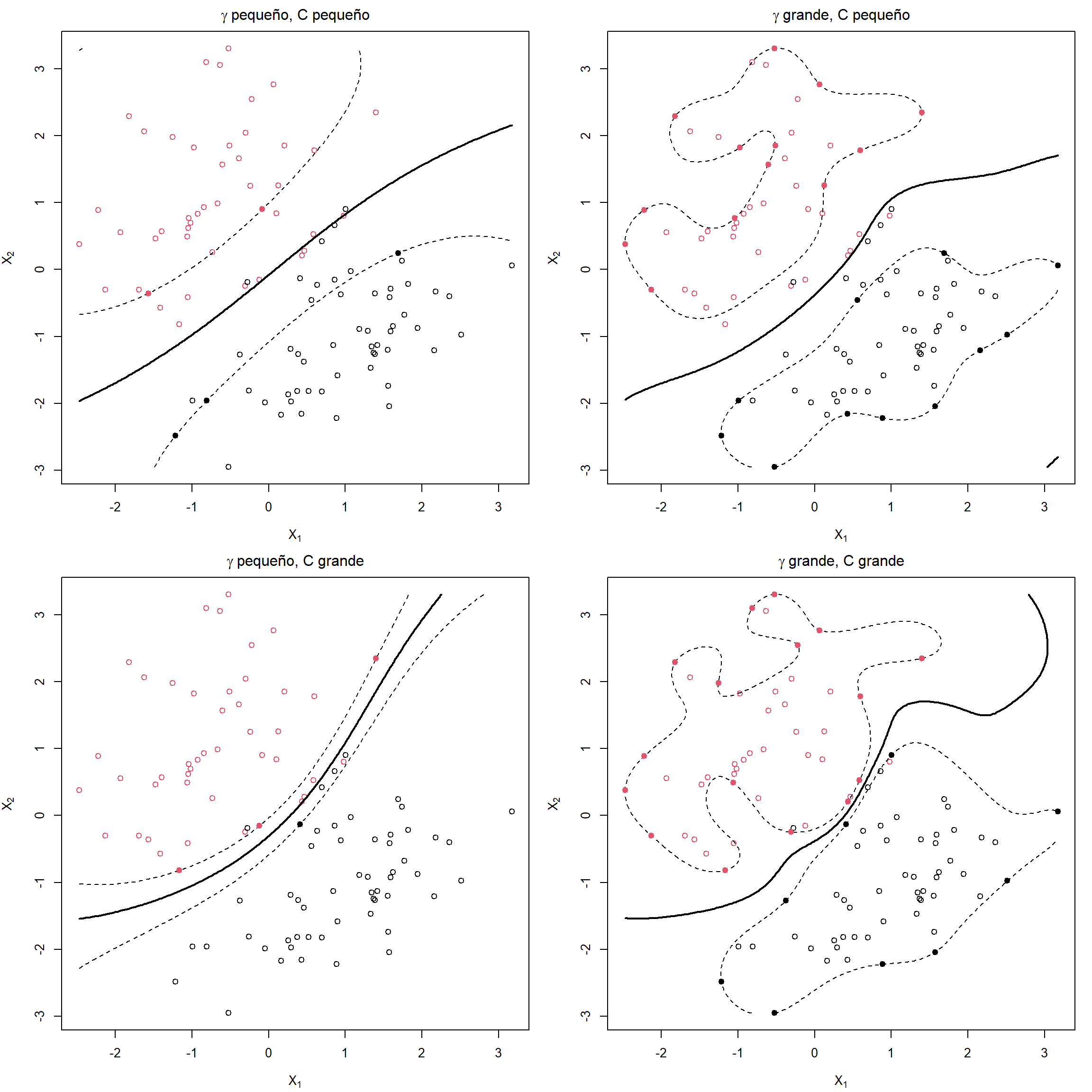
Figura 5.3: Ejemplos de máquinas de soporte vectorial con diferentes valores de los hiperparámetros (\(\gamma\) inverso de la ventana de la función kernel y coste \(C\)).
La metodología support vector machine está específicamente diseñada para clasificar cuando hay exactamente dos categorías. En la literatura se pueden encontrar varias propuestas para extenderla al caso multiclase (más de dos categorías), siendo las dos opciones más populares las comentadas en la Sección 1.2.1: “uno contra todos” (One-vs-Rest, OVR) y “uno contra uno” (One-vs-One, OVO)50.
5.3.1 Regresión con SVM
Aunque la metodología SVM está concebida para problemas de clasificación, ha habido varios intentos para adaptar su filosofía a problemas de regresión. En esta sección vamos a comentar de forma general, sin entrar en detalles, el planteamiento de Drucker et al. (1997), con un fuerte enfoque en la robustez. Recordemos que, en el contexto de la clasificación, el modelo SVM depende de unos pocos datos: los vectores soporte. En regresión, si se utiliza RSS como criterio de error, todos los datos van a influir en el modelo y, además, al estar los errores elevados al cuadrado, los valores atípicos van a tener mucha influencia, muy superior a la que tendrían si se utilizase, por ejemplo, el valor absoluto. Una alternativa, poco intuitiva pero efectiva, es fijar los hiperparámetros \(\epsilon,c > 0\) como umbral y coste, respectivamente, y definir la función de pérdidas \[ L_{\epsilon,c} (x) = \left\{ \begin{array}{ll} 0 & \mbox{si } |x|< \epsilon \\ (|x| - \epsilon)c & \mbox{en otro caso} \end{array} \right. \]
En un problema de regresión lineal, SVM estima los parámetros del modelo \[m(\mathbf{x}) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p\] minimizando \[\sum_{i=1}^n L_{\epsilon,c} (y_i - \hat y_i) + \sum_{j=1}^p \beta_j^2\]
Para hacer las cosas aún más confusas, hay autores que utilizan una formulación, equivalente, en la que el parámetro aparece en el segundo sumando como \(\lambda = 1/c\). En la práctica, es habitual fijar el valor de \(\epsilon\) y seleccionar el valor de \(c\) (equivalentemente, \(\lambda\)) utilizando, por ejemplo, validación cruzada.
El modelo puede escribirse en función de los vectores soporte, que son aquellas observaciones cuyo residuo excede el umbral \(\epsilon\): \[m(\mathbf{x}) = \beta_0 + \sum_{i\in S} \alpha_i \mathbf{x}^t \mathbf{x}_i\]
Finalmente, utilizando una función kernel, el modelo de regresión SVM se expresa como \[m(\mathbf{x}) = \beta_0 + \sum_{i\in S} \alpha_i K(\mathbf{x}, \mathbf{x}_i)\]
5.3.2 Ventajas e incovenientes
A modo de conclusión, veamos las principales ventajas e inconvenientes de las máquinas de soporte vectorial.
Ventajas:
Son muy flexibles, ya que pueden adaptarse a fronteras no lineales complejas, por lo que en muchos casos se obtienen buenas predicciones.
Al suavizar el margen, utilizando un parámetro de coste \(C\), son relativamente robustas frente a valores atípicos.
Inconvenientes:
Los modelos ajustados son difíciles de interpretar (son una caja negra), por lo que habría que recurrir a herramientas generales como las descritas en la Sección 1.5.
Pueden requerir mucho tiempo de computación cuando \(n >> p\), ya que hay que estimar (en principio) tantos parámetros como número de observaciones hay en los datos de entrenamiento, aunque finalmente la mayoría de ellos se anularán (en cualquier caso es necesario factorizar la matriz \(K_{ij} = K(\mathbf{x}_i, \mathbf{x}_j)\) de dimensión \(n \times n\)).
Están diseñados para predictores numéricos, ya que emplean distancias, por lo que para utilizar variables explicativas categóricas habrá que realizar un preprocesado, transformándolas en variables indicadoras.