7.4 Métodos Monte Carlo en Inferencia Estadística

Work in progress: Esta sección es muy preliminar y variará en siguientes ediciones.

Como ya se comentó en la introducción muchas de las aplicaciones de la simulación serían de utilidad en Estadística:

  • Distribución de estimadores puntuales/estadísticos:

    • Aproximación de la distribución.

      • Aproximación de características de la distribución.

      • Valided de la distribución asintótica.

    • Comparación de estimadores.

  • Estimación por intervalo de confianza:

    • Obtención de intervalos/bandas de confianza (probabilidad).

    • Análisis de un estimador por intervalo de confianza.

  • Contrastes de hipótesis:

    • Aproximación del \(p\)-valor.

    • Análisis de un contraste de hipótesis.

    • Validación teoría.

  • Métodos de remuestro bootstrap.

  • Inferencia Bayesiana

  • …

En esta sección nos centraremos en estudios de simulación Monte Carlo en algunas de estas aplicaciones y daremos algún ejemplo de métodos Monte Carlo para inferencia estadística. La mayoría de los métodos Monte Carlo los podríamos clasificar como métodos de remuestreo y se tratarán con mayor profundidad en capítulos siguientes.

Observación: En esta sección se obtendrán simulaciones de estadísticos a partir de muestras (podemos pensar que se parte de generaciones de una variable multivariante). En la mayoría de los ejemplos se generan todas las muestras de una vez, se guardan y se procesan vectorialmente (normalmente empleando la función apply). Como ya se comentó en el Capítulo 1.3, en problemas mas complejos, en los que no es necesario almacenar todas las muestras, puede ser preferible emplear un bucle para generar y procesar las muestras iterativamente.

7.4.1 Distribución en el muestreo

Ejercicio 7.2 (Distribución de la media muestral)

Si \(X_{1},\ldots,X_{n}\) es una muestra aleatoria simple de una variable aleatoria \(X \sim N\left( \mu, \sigma \right)\), la distribución en el muestreo de: \[\hat{\mu}=\overline{X}=\dfrac{1}{n}\sum_{i=1}^{n}X_{i}\] es: \[\overline{X} \sim N\left( \mu,\dfrac{\sigma}{\sqrt{n}}\right)\] Confirmar este resultado mediante simulación, para ello:

  1. Crear un conjunto de datos muestras con 500 muestras de tamaño \(n=10\) de una \(N(1,2)\). Añadir al conjunto de datos las estimaciones de la media y desviación típica obtenidas con cada una de las muestras.

    Valores iniciales:

    set.seed(54321) # Fijar semilla para reproducibilidad
nsim <- 500
nx <- 10

    Valores teóricos:

    mux <- 1
sdx <- 2

    Simulación de las muestras (al estilo Rcmdr):

    muestras <- as.data.frame(matrix(rnorm(nsim*nx, mean=mux, sd=sdx), ncol=nx))
rownames(muestras) <- paste("muestra", 1:nsim, sep="")
colnames(muestras) <- paste("obs", 1:nx, sep="")
str(muestras)
    ## 'data.frame':    500 obs. of  10 variables:
##  $ obs1 : num  0.642 -0.856 -0.568 -2.301 0.184 ...
##  $ obs2 : num  3.483 2.216 1.1 4.305 0.677 ...
##  $ obs3 : num  1.24 -1.51 -3.98 2.29 2.46 ...
##  $ obs4 : num  3.286 0.947 0.953 -1.663 2.623 ...
##  $ obs5 : num  3.77 -1.34 1.61 -2.46 1.11 ...
##  $ obs6 : num  -2.044 0.32 3.046 0.136 3.555 ...
##  $ obs7 : num  0.6186 -1.8614 4.3386 0.0996 0.8334 ...
##  $ obs8 : num  -0.829 2.202 -1.688 1.534 -0.114 ...
##  $ obs9 : num  0.4904 -0.6713 0.5451 -0.6517 0.0168 ...
##  $ obs10: num  2.79 2.84 1.27 3.93 2.17 ...

    Estimaciones:

    muestras$mean <- rowMeans(muestras[,1:nx])
muestras$sd <- apply(muestras[,1:nx], 1, sd)

    La fila muestras[i,] contiene las observaciones de la i-ésima muestra y la correspondiente media y desviación típica.

    muestras[1,]
    ##               obs1     obs2     obs3    obs4     obs5     obs6      obs7
## muestra1 0.6421985 3.482661 1.242483 3.28559 3.766896 -2.04443 0.6186323
##                obs8      obs9    obs10     mean       sd
## muestra1 -0.8293636 0.4903819 2.790091 1.344514 1.951292

Normalmente emplearemos sin embargo una ordenación por columnas (cada fila se corresponderá con una generación).

  1. Generar el histograma (en escala de densidades) de las medias muestrales y compararlo con la densidad teórica.

    Distribución de la media muestral:

    hist(muestras$mean, freq = FALSE, breaks = "FD", 
     xlab = "Medias", ylab = "Densidad")
# Densidad observada (estimación)
lines(density(muestras$mean)) 
# Densidad teórica (bajo normalidad)
curve(dnorm(x, mux, sdx/sqrt(nx)), lwd = 2, col = "blue", add = TRUE) 
# Aproximación del valor esperado de la media muestral mediante simulación
abline(v = mean(muestras$mean), lty = 2)  
# Valor esperado de la media muestral (teórico)
abline(v = mux, col = "blue")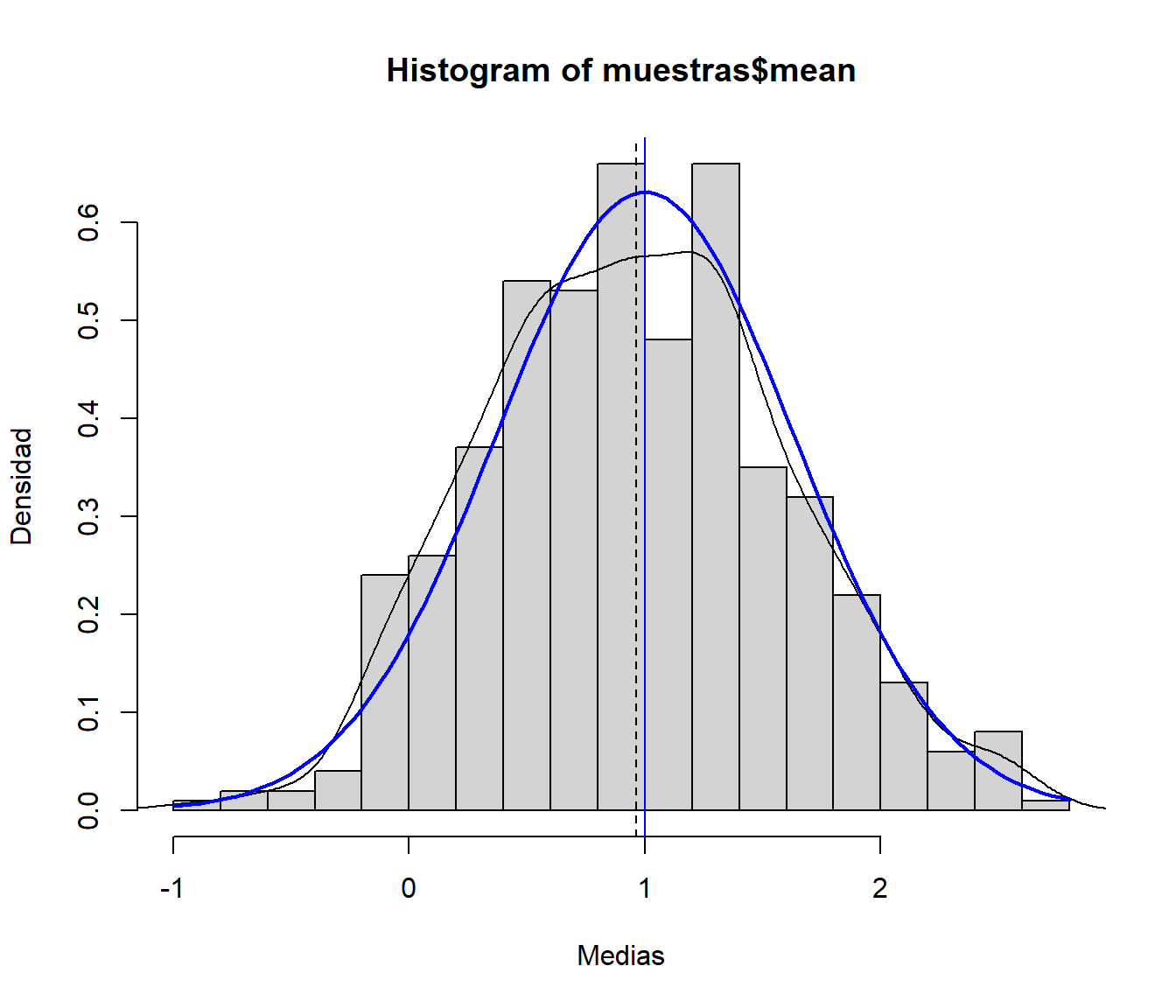
    Distribución de la media muestral de una distribución normal.

    Figura 7.9: Distribución de la media muestral de una distribución normal.


Ejercicio 7.3 (Distribución de la media muestral continuación)

Si \(X_{1},\ldots,X_{n}\) es una m.a.s. de una variable aleatoria \(X\) (cualquiera) con \(E\left( X \right) = \mu\) y \(Var\left( X \right) = \sigma^{2}\), por el Teorema Central del Límite, la distribución en el muestreo de \(\hat{\mu}=\overline{X}\) se aproxima a la normalidad: \[\overline{X}\underset{n\rightarrow\infty}{\longrightarrow} N\left( \mu, \dfrac{\sigma}{\sqrt{n}}\right)\] Típicamente se suele considerar que esta aproximación es buena para tamaños muestrales \(n>30\), aunque dependerá de las características de la distribución de \(X\).

  1. Repetir el Ejercicio 7.2 anterior considerando muestras de una \(Exp(1)\) (tener en cuenta que \(X\sim Exp(\lambda)\Rightarrow\mu_{X}=\sigma_{X}=1/\lambda\)). ¿Qué ocurre con la distribución de la media muestral?

    set.seed(54321) # Fijar semilla para reproducibilidad
nsim <- 500
nx <- 10    
# nx <- 50

    Valores teóricos:

    lambda <- 1
muexp <- 1/lambda
sdexp <- muexp

    Simulación de las muestras:

    muestras2 <- as.data.frame(matrix(rexp(nsim*nx, rate=lambda), ncol=nx))
rownames(muestras2) <- paste("muestra", 1:nsim, sep="")
colnames(muestras2) <- paste("obs", 1:nx, sep="")

    Estimaciones:

    muestras2$mean <- rowMeans(muestras2[,1:nx])
muestras2$sd <- apply(muestras2[,1:nx], 1, sd)

    Distribución de la media muestral:

    hist(muestras2$mean, xlim = c(-0.1, 2.5), freq = FALSE, breaks = "FD", 
     xlab = "Medias", ylab = "Densidad")
# Densidad observada (estimación)
lines(density(muestras2$mean)) 
# Distribución asintótica (TCL)
curve(dnorm(x,muexp,sdexp/sqrt(nx)), lwd=2, col="blue", add=TRUE) 
# Aproximación del valor esperado de la media muestral mediante simulación
abline(v=mean(muestras2$mean),lty=2)  
# Valor esperado de la media muestral (teórico)
abline(v=muexp, col="blue")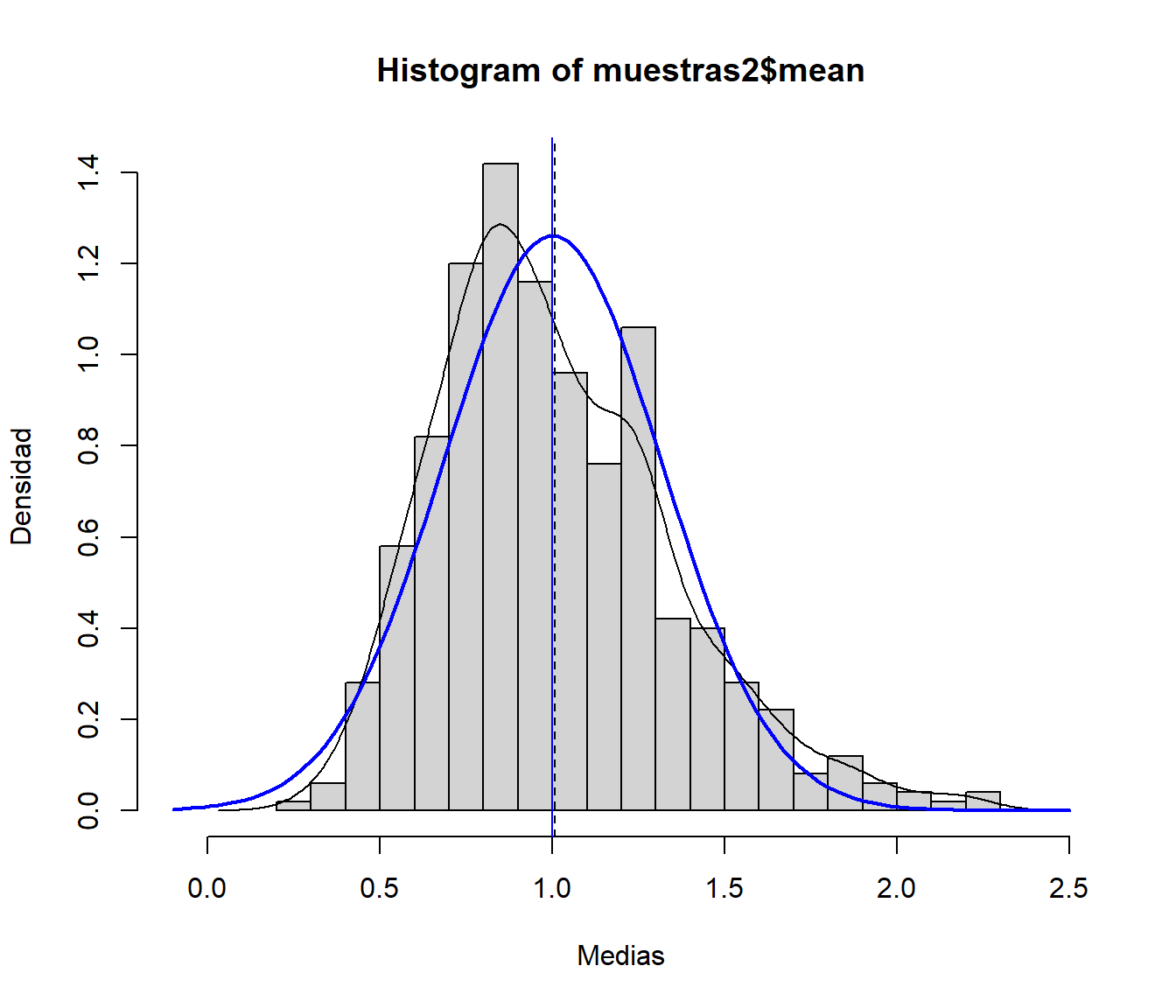
    Distribución de la media muestral de una distribución exponencial y distribución asintótica.

    Figura 7.10: Distribución de la media muestral de una distribución exponencial y distribución asintótica.

  2. Aumentar el tamaño muestral a 50. ¿Se aproxima más la distribución de las medias muestrales a la teórica bajo normalidad?

    Ejecutar el código del apartado anterior fijando nx <- 50.

7.4.2 Intervalos de confianza

Ejercicio 7.4 (Intervalo de confianza para la media)

A partir del enunciado del Ejercicio 7.2, se deduce que el intervalo de confianza (de nivel \(1-\alpha\)) para la media \(\mu\) de una población normal con varianza conocida es: \[IC_{1-\alpha}\left( \mu\right) = \left( \overline{X}-z_{1-\alpha/2}\dfrac{\sigma}{\sqrt{n}},\ \overline{X} + z_{1-\alpha/2}\dfrac{\sigma}{\sqrt{n}} \right).\] La idea es que el \(100(1-\alpha)\%\) de los intervalos así construidos contentrán el verdadero valor del parámetro.

  1. Utilizando el conjunto de datos muestras del ejercicio 1 (500 muestras de tamaño \(n=10\) de una \(N(1,2)\)), añadir en dos nuevas variables los extremos del intervalo de confianza para la media con varianza conocida al conjunto de datos. Analizar la cobertura de estas estimaciones por IC.

    IC para la media con varianza conocida (bajo normalidad):

    alfa <- 0.05
z <- qnorm(1 - alfa/2)
muestras$ici <- muestras$mean - z*sdx/sqrt(nx)
muestras$ics <- muestras$mean + z*sdx/sqrt(nx)

    Cobertura de las estimaciones por IC:

    muestras$cob <- (muestras$ici < mux) & (mux < muestras$ics) 
ncob <- sum(muestras$cob) # Nº de intervalos que contienen la verdadera media
ncob
    ## [1] 480
    100*ncob/nsim     # Proporción de intervalos
    ## [1] 96
    100*(1 - alfa)    # Proporción teórica bajo normalidad
    ## [1] 95

    Como ejemplo ilustrativo, generamos el gráfico de los primeros 50 intervalos:

    m <- 50
tmp <- muestras[1:m,]
attach(tmp)
color <- ifelse(cob,"blue","red")
plot(1:m, mean, col = color, ylim = c(min(ici),max(ics)), 
     xlab = "Muestra", ylab = "IC")
arrows(1:m, ici, 1:m, ics, angle = 90, length = 0.05, code = 3, col = color)
abline(h = mux, lty = 3)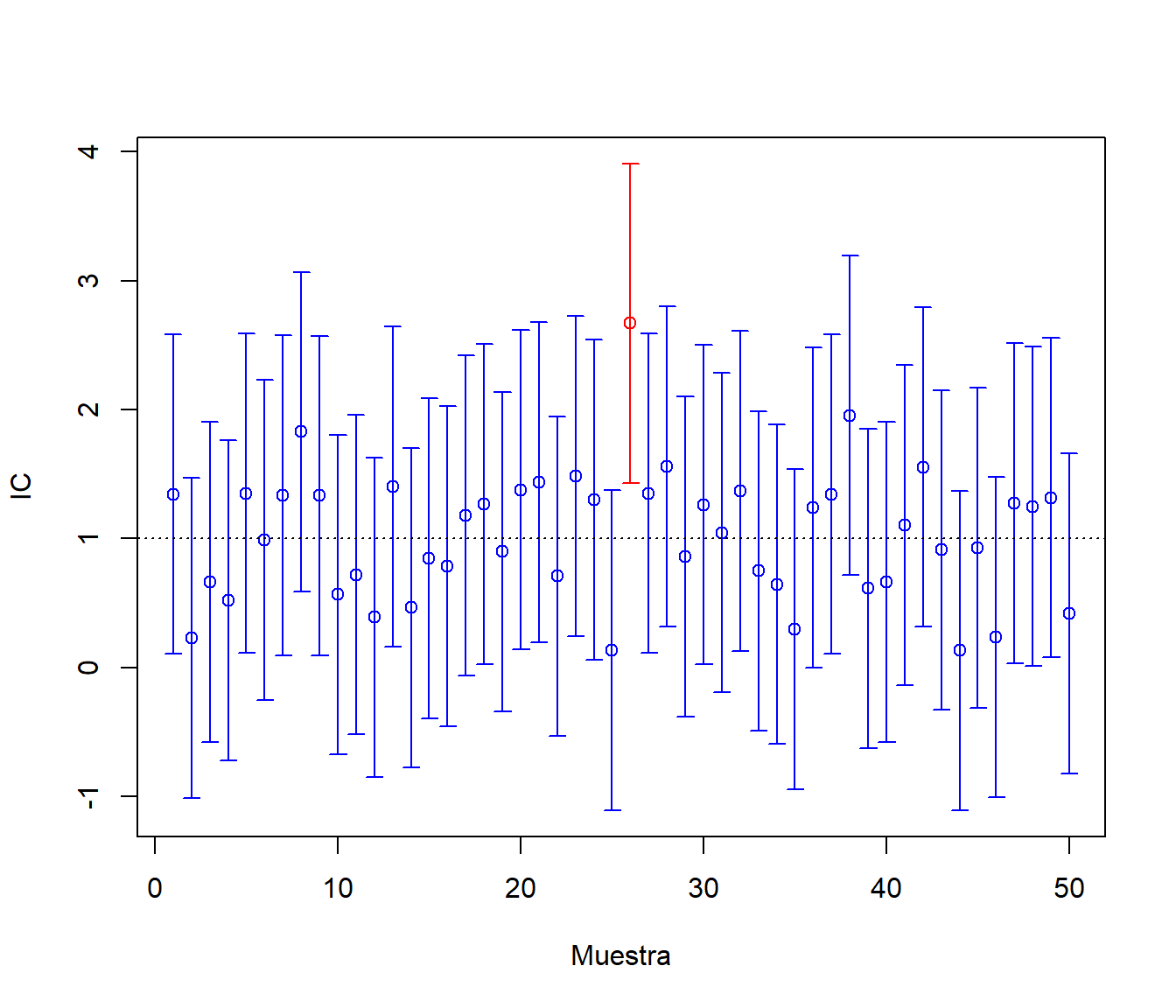
    Cobertura de las estimaciones por IC.

    Figura 7.11: Cobertura de las estimaciones por IC. 

    detach(tmp)

  2. Repetir el apartado anterior considerando muestras de una \(Exp(1)\). ¿Qué ocurre con la cobertura del intervalo de confianza obtenido bajo normalidad?

    Ejecutar el código del apartado a) del ejercicio 2.

    IC para la media con varianza conocida (bajo normalidad)

    alfa <- 0.05
z <- qnorm(1 - alfa/2)
muestras2$ici <- muestras2$mean - z*sdexp/sqrt(nx)
muestras2$ics <- muestras2$mean + z*sdexp/sqrt(nx)

    Cobertura de las estimaciones por IC:

    muestras2$cob <- (muestras2$ici < muexp) & (muexp < muestras2$ics) 
ncob <- sum(muestras2$cob) # Nº de intervalos que contienen la verdadera media
ncob
    ## [1] 469
    100*ncob/nsim     # Proporción de intervalos
    ## [1] 93.8
    100*(1 - alfa)    # Proporción teórica bajo normalidad
    ## [1] 95

    Como ejemplo ilustrativo, generamos el gráfico de los primeros 100 intervalos:

    m <- 100
tmp <- muestras2[1:m,]
attach(tmp)
color <- ifelse(cob,"blue","red")
plot(1:m, mean, col = color, ylim = c(min(ici),max(ics)), 
     xlab = "Muestra", ylab = "IC")
arrows(1:m, ici, 1:m, ics, angle = 90, length = 0.05, code = 3, col = color)
abline(h = muexp, lty = 3)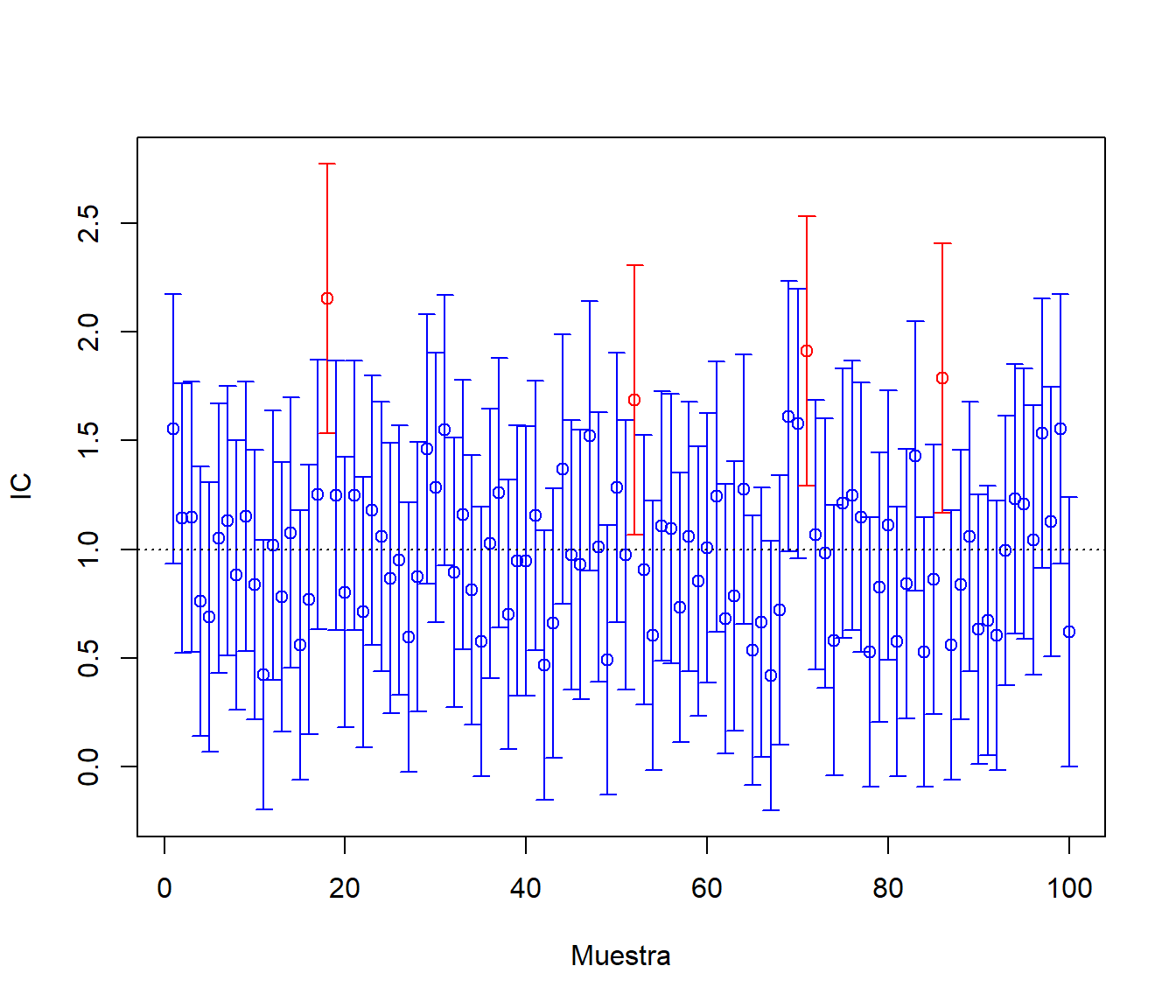
    Cobertura de las estimaciones por IC (bajo normalidad).

    Figura 7.12: Cobertura de las estimaciones por IC (bajo normalidad). 

    detach(tmp)

  3. ¿Qué ocurre si aumentamos el tamaño muestral a 50?

    Ejecutar el código del ejercicio anterior fijando nx <- 50 y el del apartado anterior.

En los apartados b) y c) podíamos considerar bootstrap descrito en siguientes capítulos.

Podemos aproximar por simulación los intervalos de probabilidad de la media muestral (tendríamos una idea del valor esperado de lo que obtendríamos con el bootstrap percentil; en este caso el estimador es insesgado…):

# Distribución de la media muestral
hist(muestras2$mean, freq=FALSE, breaks="FD", 
     main="Distribución de la media muestral", xlab="Medias", ylab="Densidad")
# Densidad observada (estimación)
lines(density(muestras2$mean), lwd=2, col='red') 
# Densidad teórica (bajo normalidad)
curve(dnorm(x,muexp,sdexp/sqrt(nx)), col="blue", add=TRUE) 
# Aproximación por simulación del valor esperado de la media muestral
abline(v=mean(muestras2$mean), lty=2)
# Valor esperado de la media muestral (teórico)
abline(v=muexp, col="blue") 
# IP bajo normalidad
ic.aprox <- apply(muestras2[ ,c('ici','ics')], 2, mean)
## ic.aprox 
##       ici       ics 
## 0.3865199 1.6261099
# Intervalo de probabilidad para la media muestral aproximado bajo normalidad
abline(v = ic.aprox, col='blue')

# Intervalo de probabilidad para la media muestral (aproximado por simulación)
ic.sim <- quantile(muestras2$mean, c(alfa/2, 1 - alfa/2))
## ic.sim
##      2.5%     97.5% 
## 0.4714233 1.8059094
# IP (aprox.) 
abline(v=ic.sim, lty=2, col='red')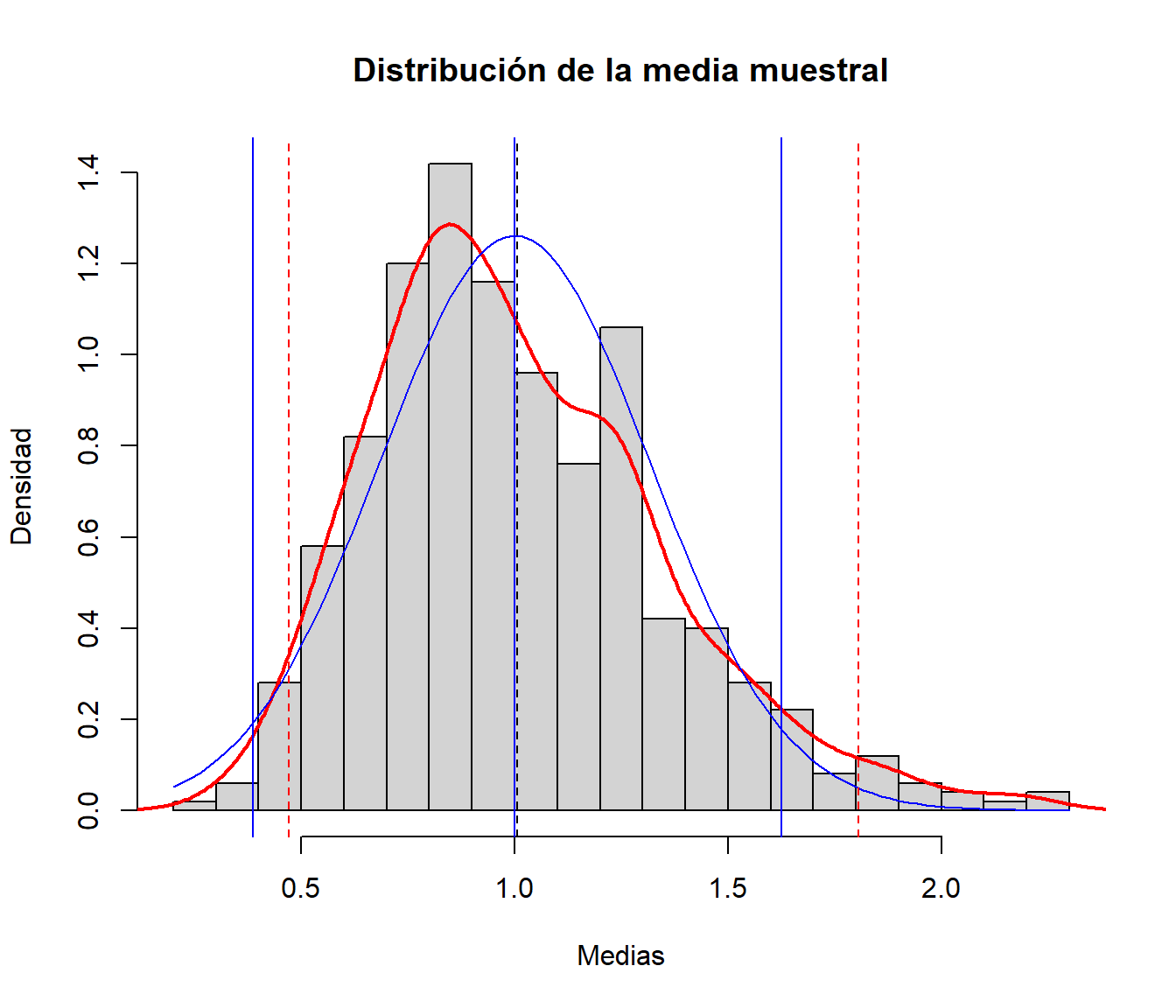

Nota:. Estimaciones puntuales, por intervalo de confianza y contrastes de hipótesis para la media con varianza desconocida bajo normalidad se pueden obtener con la función t.test.


Ejercicio 7.5 (Intervalo de confianza Agresti-Coull para una proporción)

El Intervalo de confianza para una proporción construido usando la aproximación normal tiene un mal comportamiento cuando el tamaño de la muestra es pequeño. Una simple y efectiva mejora consiste en añadir a la muestra \(2a\) elementos, \(a\) exitos y \(a\) fracasos. Así el intervalo de confianza al \(\left( 1-\alpha\right) 100\%\) para una proporción mejorado es: \[\begin{aligned} IC_{1-\alpha}^{a}\left( p\right) & =\left( \tilde{p}-z_{1-\alpha/2}\sqrt{\frac{\tilde{p}(1-\tilde{p})}{\tilde{n}}} \text{ , } \tilde{p}+z_{1-\alpha/2}\sqrt{\frac{\tilde{p}(1-\tilde{p})}{\tilde{n}}}\right) ,\\ \text{siendo }\tilde{n} & = n+2a \text{, } \tilde{p} = \frac{np+a}{\tilde{n}}. \end{aligned}\] En el caso de \(a=2\) se denomina IC Agresti-Coull.

(Los apartados a) y b) están basados en los ejemplos 1.5 y 1.6 de Suess y Trumbo, 2010)

  1. Teniendo en cuenta que la variable aleatoria \(X=n\hat{p}\sim\mathcal{B}(n,p)\), obtener y representar gráficamente la cobertura teórica del intervalo de confianza estándar (\(a=0\)) de una proporción para una muestra de tamaño \(n=30\), \(\alpha=0.05\) y distintos valores de \(p\) (p.teor <- seq(1/n, 1 - 1/n, length = 1000)).

    Parámetros:

    n <- 30
alpha <- 0.05
adj <- 0  # (adj <- 2 para Agresti-Coull)

    Probabilidades teóricas:

    m <- 1000
p.teor <- seq(1/n, 1 - 1/n, length = m)

    Posibles resultados:

    x <- 0:n
p.est <- (x + adj)/(n + 2 * adj) 
ic.err <- qnorm(1 - alpha/2) * sqrt(p.est * (1 - p.est)/(n + 2 * adj))  
lcl <- p.est - ic.err 
ucl <- p.est + ic.err

    Recorrer prob. teóricas:

    p.cov <- numeric(m)
for (i in 1:m) {
  # cobertura de los posibles intervalos
  cover <- (p.teor[i] >= lcl) & (p.teor[i] <= ucl)  
  # prob. de los posibles intervalos
  p.rel <- dbinom(x[cover], n, p.teor[i])           
  # prob. total de cobertura
  p.cov[i] <- sum(p.rel)                            
}

    Gráfico coberturas:

    plot(p.teor, p.cov, type = "l", ylim = c(1 - 4 * alpha, 1))
abline(h = 1 - alpha, lty = 2)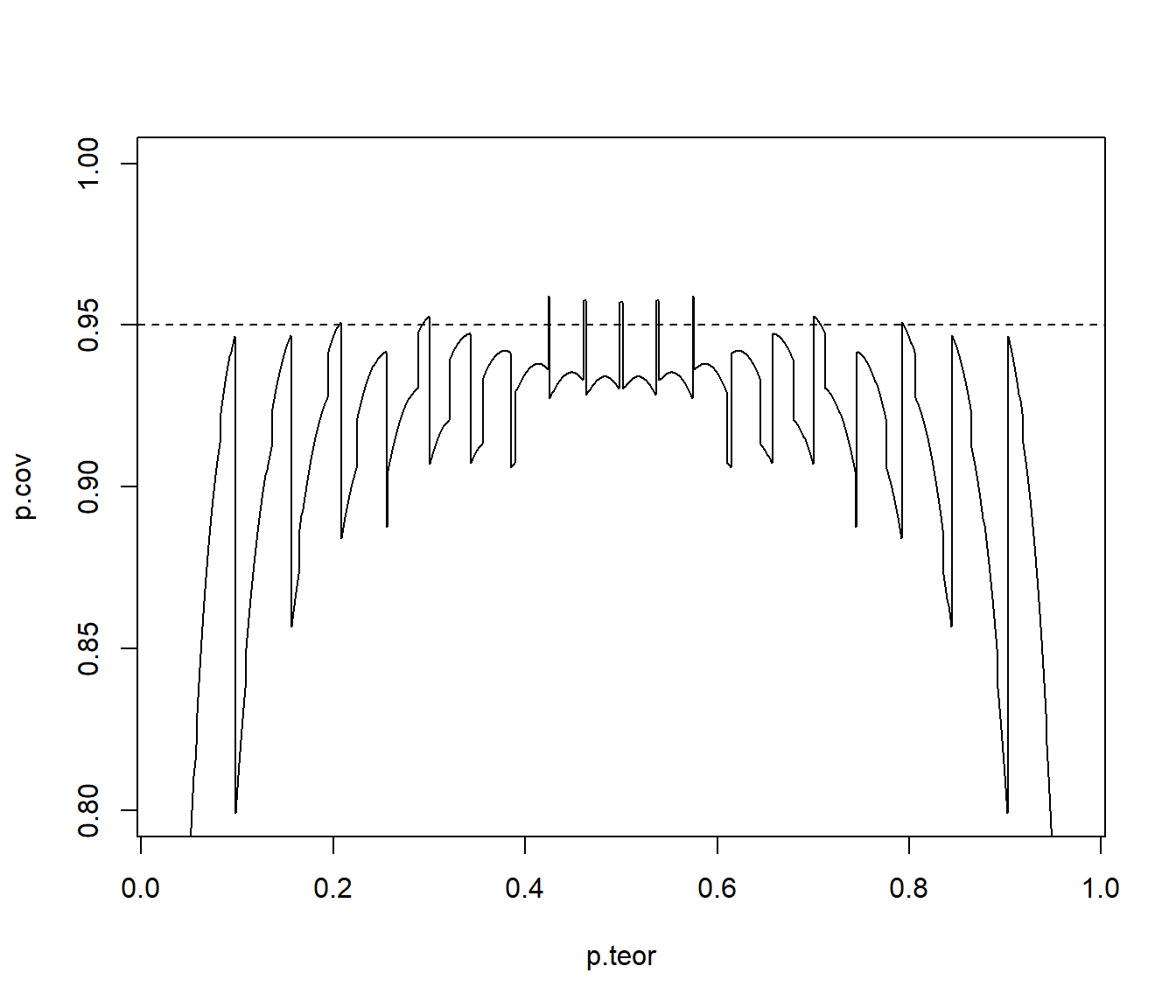

    Fuente Suess y Trumbo (2010).

  2. Repetir el apartado anterior considerando intervalos de confianza Agresti-Coull (\(a=2\)).

    Parámetros:

    n <- 30
alpha <- 0.05
adj <- 2  # Agresti-Coull

# Probabilidades teóricas:
m <- 1000
p.teor <- seq(1/n, 1 - 1/n, length = m) 
# Posibles resultados:
x <- 0:n
p.est <- (x + adj)/(n + 2 * adj) 
ic.err <- qnorm(1 - alpha/2) * sqrt(p.est * (1 - p.est)/(n + 2 * adj))  
lcl <- p.est - ic.err 
ucl <- p.est + ic.err 
# Recorrer prob. teóricas:
p.cov <- numeric(m)
for (i in 1:m) {
  # cobertura de los posibles intervalos
  cover <- (p.teor[i] >= lcl) & (p.teor[i] <= ucl)  
  # prob. de los posibles intervalos
  p.rel <- dbinom(x[cover], n, p.teor[i])           
  # prob. total de cobertura
  p.cov[i] <- sum(p.rel)                            
}
# Gráfico coberturas:
plot(p.teor, p.cov, type = "l", ylim = c(1 - 4 * alpha, 1))
abline(h = 1 - alpha, lty = 2)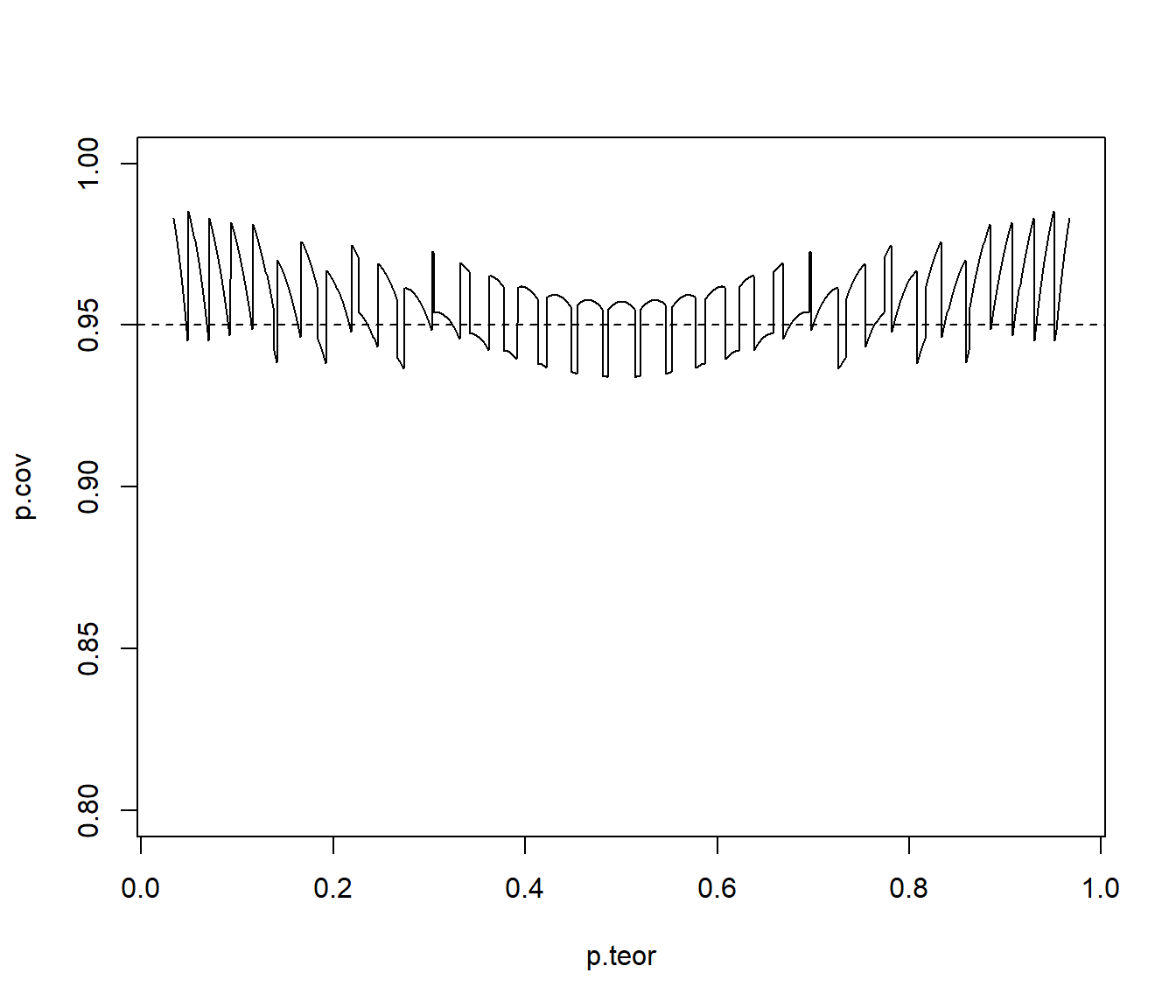

  3. Repetir el apartado anterior empleando simulación para aproximar la cobertura.

    Parámetros:

    n <- 30
alpha <- 0.05
adj <- 2  #' (2 para Agresti-Coull)

set.seed(54321)
nsim <- 500 
# Probabilidades teóricas:
m <- 1000
p.teor <- seq(1/n, 1 - 1/n, length = m)

    Recorrer prob. teóricas:

    # m <- length(p.teor)
p.cov <- numeric(m)
for (i in 1:m) {
  # Equivalente a simular nsim muestras de tamaño n
  # ry <- matrix(rbinom(n*nsim, 1, p.teor[i]), ncol=n)
  # rx <- apply(ry, 1, sum)
  rx <- rbinom(nsim, n, p.teor[i])
  p.est <- (rx + adj)/(n + 2 * adj)  
  ic.err <- qnorm(1 - alpha/2) * sqrt(p.est * (1 - p.est)/(n + 2 * adj))
  p.cov[i] <- mean( abs(p.est - p.teor[i]) < ic.err )
}

    Representar:

    plot(p.teor, p.cov, type = "l", ylim = c(1 - 4 * alpha, 1))
abline(h = 1 - alpha, lty = 2)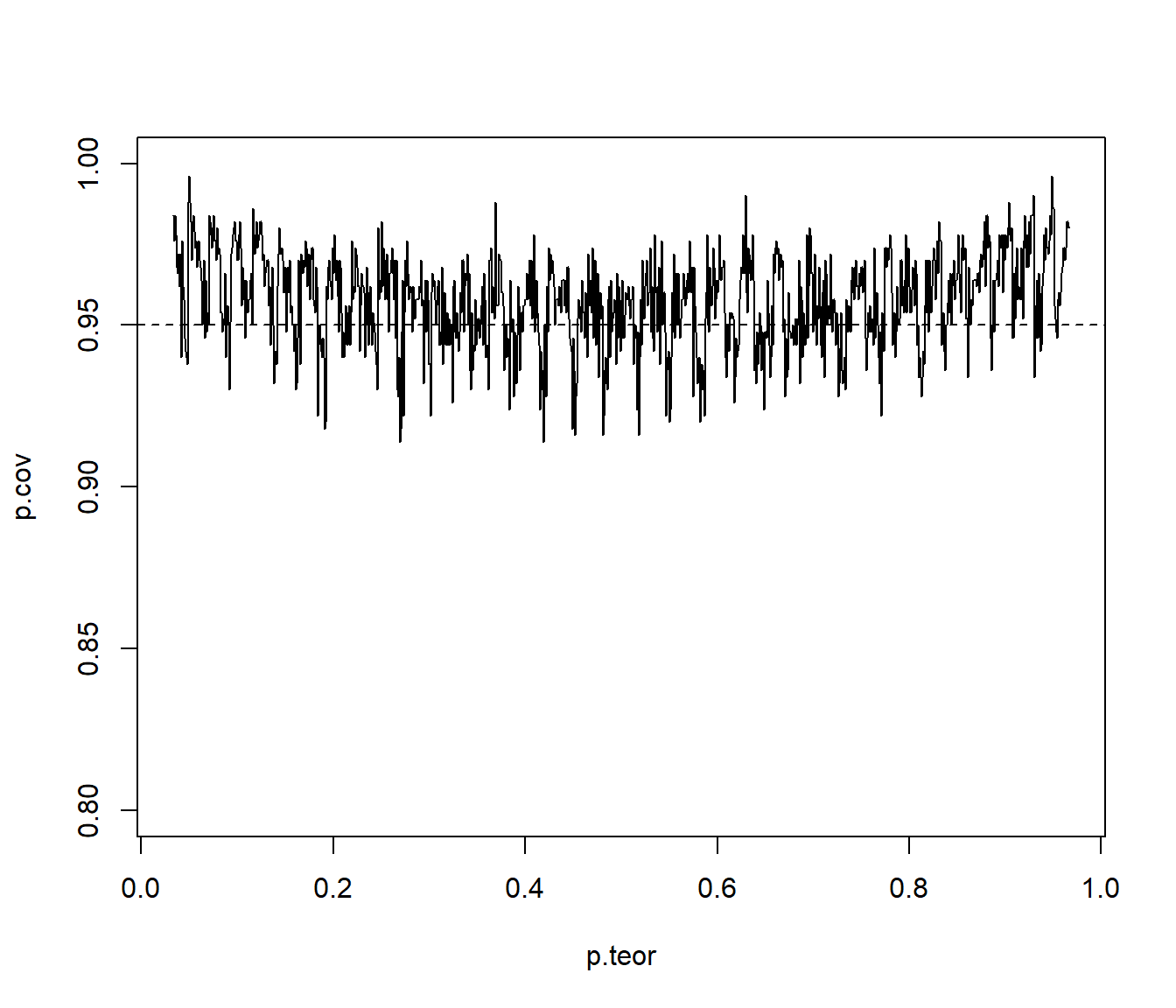

Como ya se comentó, el caso de ajustar un modelo a los datos y realizar simulaciones a partir de ese modelo ajustado para aproximar las características de interés de un estadístico, se denomina también bootstrap paramétrico. Para más detalles ver por ejemplo la Sección 3.1 de Cao y Fernández-Casal (2020). En este libro, en las secciones 4.6.2 y B.3.2, se incluyen ejemplos adicionales de estudios de simulación.

7.4.3 Contrastes de hipótesis

Ver Capítulo 5 de Cao y Fernández-Casal (2020).

Ejercicio 7.6 (Test de Kolmogorov-Smirnov)

En la Sección 2.3 del Tema 2 se propuso el análisis de la bondad de ajuste de un generador de números pseudo-aleatorios mediante el test de Kolmogorov-Smirnov (ver Sección A.1.5). Sin embargo, si \(H_{0}\) es compuesta (los parámetros desconocidos se estiman por máxima verosimilitud y se trabaja con \(\hat{F}_{0}\)) los cuantiles de la distribución (asintótica) de \(D_{n}\) pueden ser demasiado conservativos y sería preferible utilizar la distribución exacta.

  1. Analizar el comportamiento del contraste de Kolmogorov-Smirnov para contrastar normalidad empleando repetidamente este test, considerando 1000 pruebas con muestras de tamaño 30 de una \(\mathcal{N}(0,1)\). Comparar gráficamente el ajuste de la distribución del \(p\)-valor a la de referencia (estudiar el tamaño del contraste).

    Valores iniciales:

    set.seed(54321)
nx <- 30
mx <- 0
sx <- 1
nsim <- 1000
estadistico <- numeric(nsim)
pvalor <- numeric(nsim)

    Realizar contrastes

    for(isim in 1:nsim) {
  rx <- rnorm(nx, mx, sx)
  tmp <- ks.test(rx, "pnorm", mean(rx), sd(rx))
  estadistico[isim] <- tmp$statistic
  pvalor[isim] <- tmp$p.value
}

    Proporción de rechazos:

    {
  cat("\nProporción de rechazos al 1% =", mean(pvalor < 0.01), "\n")
  cat("Proporción de rechazos al 5% =", mean(pvalor < 0.05), "\n")
  cat("Proporción de rechazos al 10% =", mean(pvalor < 0.1), "\n")
}
    ## 
## Proporción de rechazos al 1% = 0 
## Proporción de rechazos al 5% = 0 
## Proporción de rechazos al 10% = 0.001

    Análisis de los p-valores:

    hist(pvalor, freq=FALSE)
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)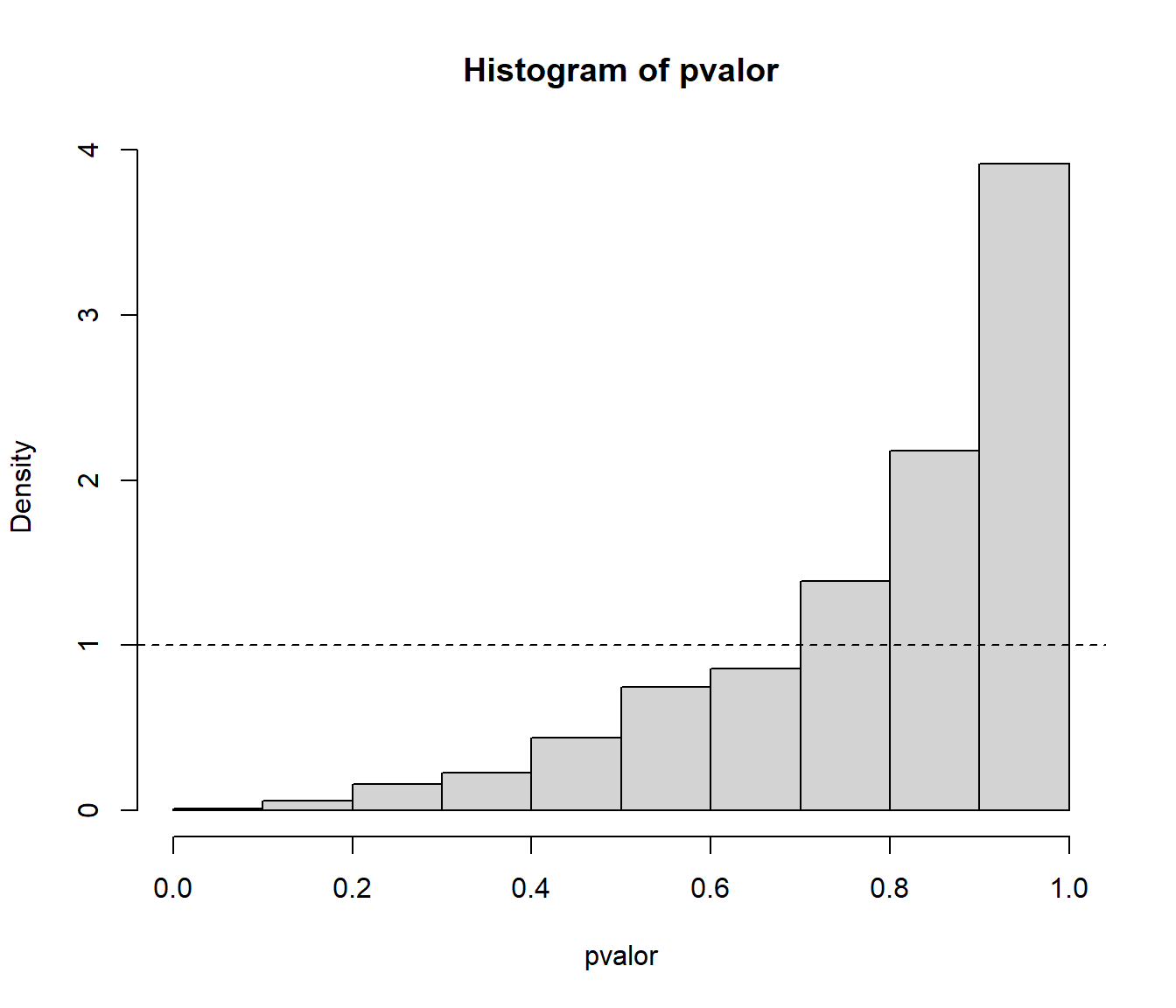

    # Distribución empírica
curve(ecdf(pvalor)(x), type = "s", lwd = 2, 
      main = 'Tamaño del contraste', ylab = 'Proporción de rechazos', 
      xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)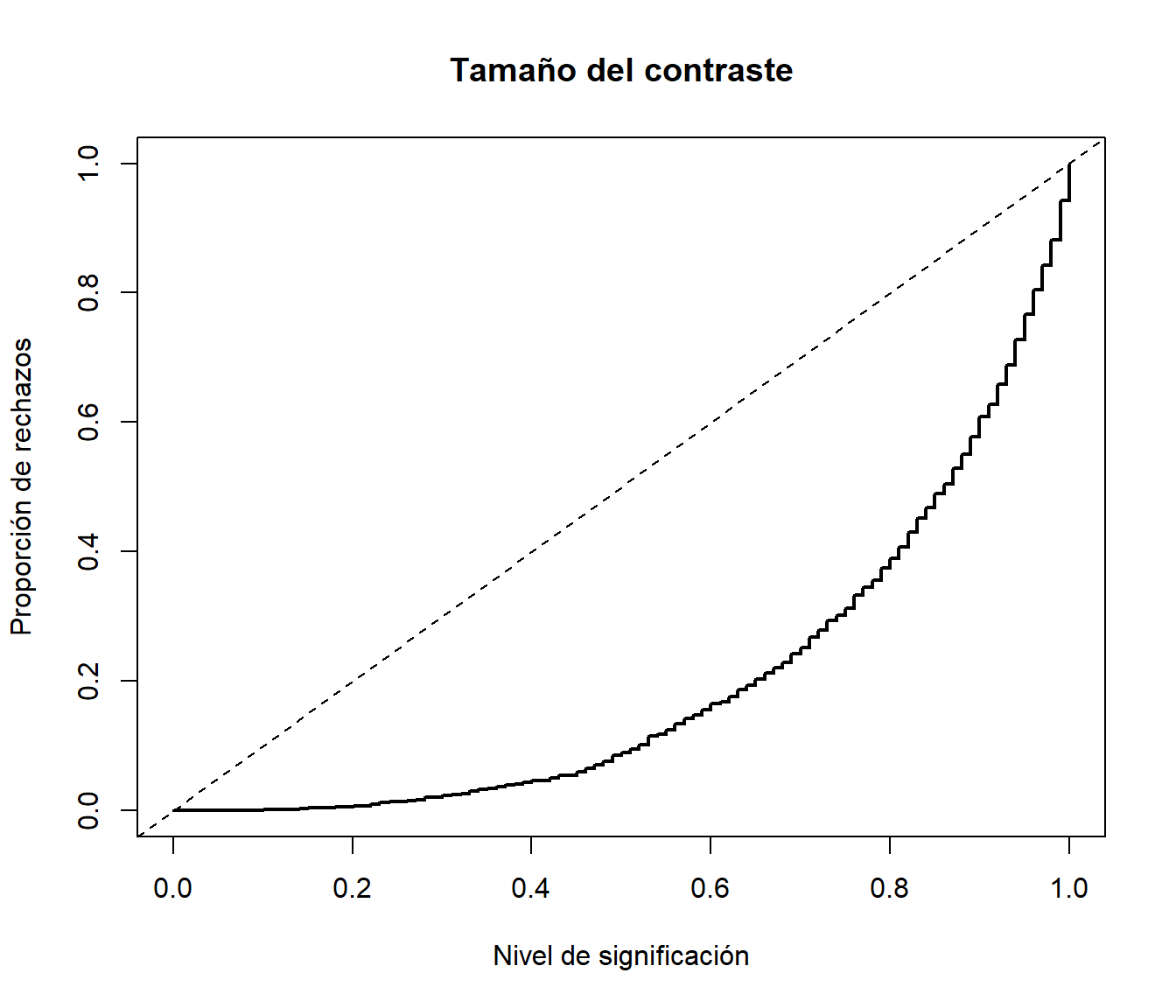

  2. Repetir el apartado anterior considerando el test de Lilliefors (rutina lillie.test del paquete nortest).

    library(nortest, quietly = TRUE)

    Valores iniciales:

    set.seed(54321)
nx <- 30
mx <- 0
sx <- 1
nsim <- 1000
estadistico <- numeric(nsim)
pvalor <- numeric(nsim)

    Realizar contrastes

    for(isim in 1:nsim) {
  rx <- rnorm(nx, mx, sx)
  # tmp <- ks.test(rx, "pnorm", mean(rx), sd(rx))
  tmp <- lillie.test(rx)
  estadistico[isim] <- tmp$statistic
  pvalor[isim] <- tmp$p.value
}

    Proporción de rechazos:

    {
  cat("\nProporción de rechazos al 1% =", mean(pvalor < 0.01), "\n")
  cat("Proporción de rechazos al 5% =", mean(pvalor < 0.05), "\n")
  cat("Proporción de rechazos al 10% =", mean(pvalor < 0.1), "\n")
}
    ## 
## Proporción de rechazos al 1% = 0.01 
## Proporción de rechazos al 5% = 0.044 
## Proporción de rechazos al 10% = 0.089

    Análisis de los p-valores:

    hist(pvalor, freq=FALSE)
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)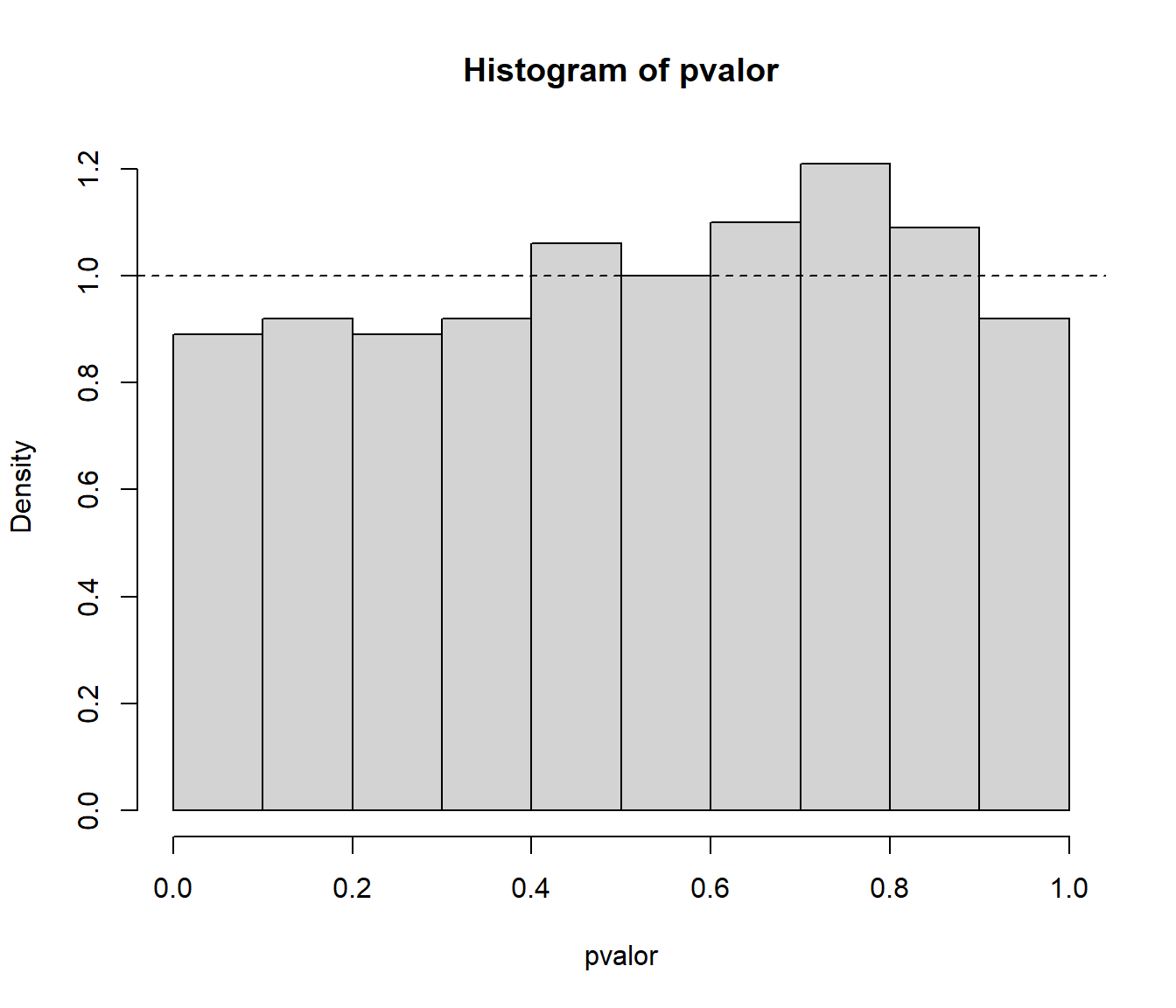

    # Distribución empírica
curve(ecdf(pvalor)(x), type = "s", lwd = 2, main = 'Tamaño del contraste', 
      ylab = 'Proporción de rechazos', xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)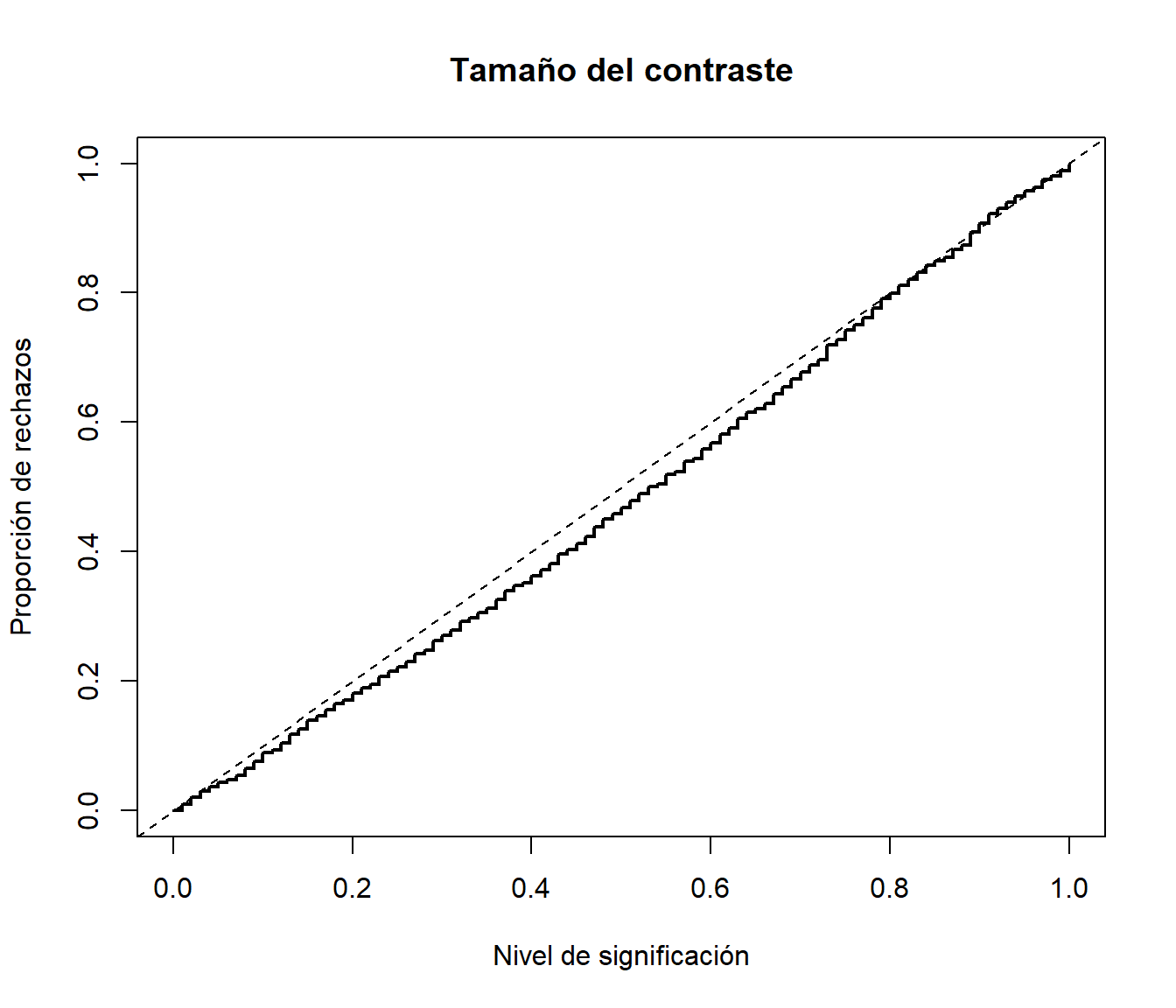

  3. Repetir el apartado a) contrastando una distribución exponencial y considerando 500 pruebas con muestras de tamaño 30 de una \(Exp(1)\).

    Valores iniciales:

    set.seed(54321)
nx <- 30
ratex <- 1
nsim <- 500
estadistico <- numeric(nsim)
pvalor <- numeric(nsim)

    Realizar contrastes

    for(isim in 1:nsim) {
  rx <- rexp(nx, ratex)
  tmp <- ks.test(rx, "pexp", 1/mean(rx))
  estadistico[isim] <- tmp$statistic
  pvalor[isim] <- tmp$p.value
}

    Proporción de rechazos:

    {
  cat("\nProporción de rechazos al 1% =", mean(pvalor < 0.01), "\n")
  cat("Proporción de rechazos al 5% =", mean(pvalor < 0.05), "\n")
  cat("Proporción de rechazos al 10% =", mean(pvalor < 0.1), "\n")
}
    ## 
## Proporción de rechazos al 1% = 0 
## Proporción de rechazos al 5% = 0.004 
## Proporción de rechazos al 10% = 0.008

    Análisis de los p-valores:

    hist(pvalor, freq=FALSE)
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)

    # Distribución empírica
curve(ecdf(pvalor)(x), type = "s", lwd = 2, 
      main = 'Tamaño del contraste', ylab = 'Proporción de rechazos', 
      xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)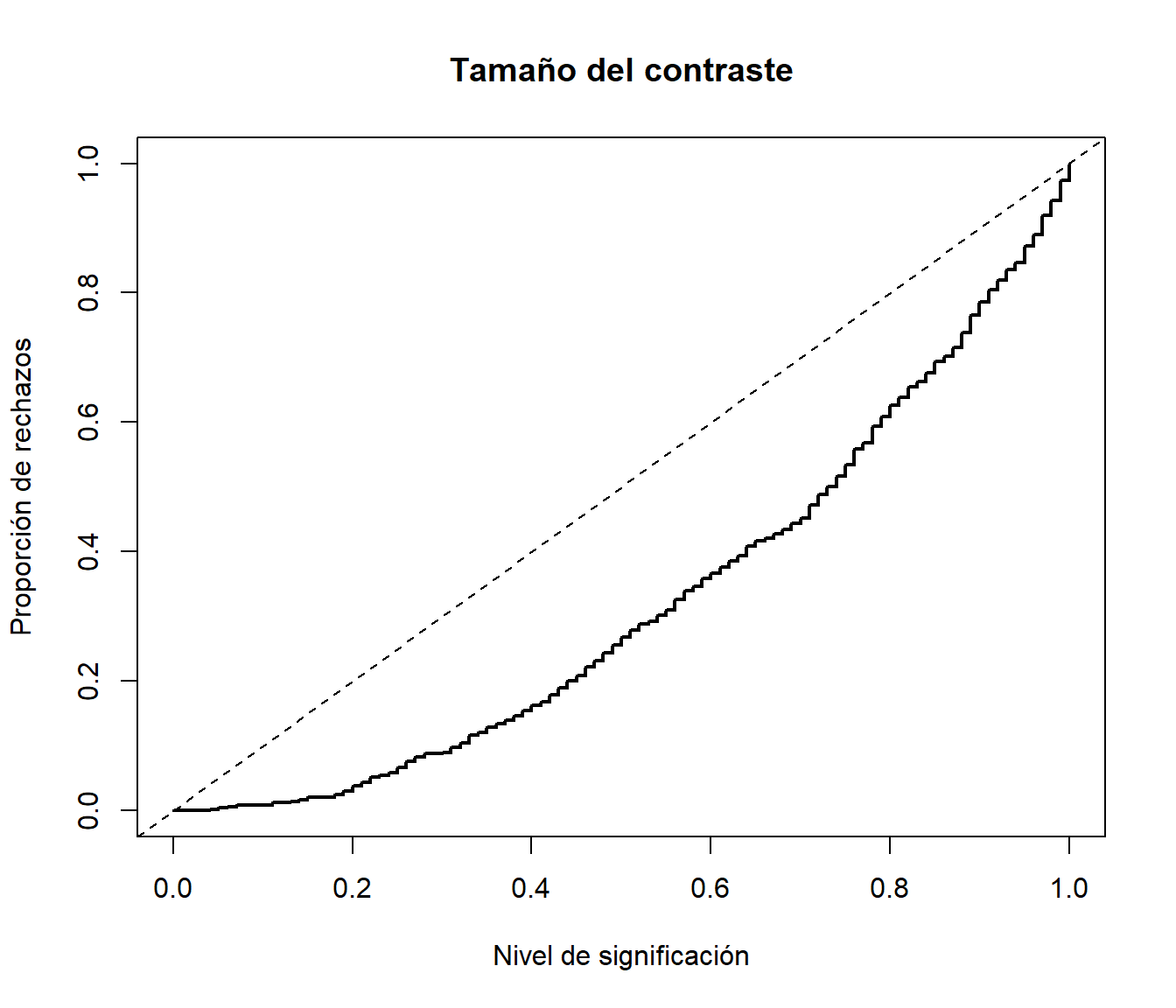

  4. Diseñar una rutina que permita realizar el contraste KS de bondad de ajuste de una variable exponencial aproximando el \(p\)-valor por simulación y repetir el apartado anterior empleando esta rutina.

    ks.exp.sim <- function(x, nsim = 10^3) {
  DNAME <- deparse(substitute(x))
  METHOD <- "Kolmogorov-Smirnov Test of pexp by simulation" 
  n <- length(x)
  RATE <- 1/mean(x)
  ks.exp.stat <- function(x, rate=1/mean(x)) {
    DMinus <- pexp(sort(x), rate=rate) - (0:(n - 1))/n
    DPlus <- 1/n - DMinus
    Dn = max(c(DMinus, DPlus))
  }  
  STATISTIC <- ks.exp.stat(x, rate = RATE) 
  names(STATISTIC) <- "Dn"
  # PVAL <- 0
  # for(i in 1:nsim) {
  #   rx <- rexp(n, rate = RATE)
  #   if (STATISTIC <= ks.exp.stat(rx)) PVAL <- PVAL+1
  # }
  # PVAL <- PVAL/nsim
  # PVAL <- PVAL/(nsim + 1)
  # PVAL <- (PVAL + 1)/(nsim + 2)
  rx <- matrix(rexp(n*nsim, rate = RATE), ncol=n)
  PVAL <- mean(STATISTIC <= apply(rx, 1, ks.exp.stat))
  return(structure(list(statistic = STATISTIC, alternative = "two.sided", 
                   p.value = PVAL, method = METHOD, data.name = DNAME), 
                   class = "htest"))
}

    Simulación:

    set.seed(54321)
nx <- 30
ratex <- 1
nsim <- 500
estadistico <- numeric(nsim)
pvalor <- numeric(nsim)

    Realizar contrastes

    for(isim in 1:nsim) {
  rx <- rexp(nx, ratex)
  # tmp <- ks.test(rx, "pexp", 1/mean(rx))
  tmp <- ks.exp.sim(rx, nsim = 200)
  estadistico[isim] <- tmp$statistic
  pvalor[isim] <- tmp$p.value
}

    Proporción de rechazos:

    {
  cat("\nProporción de rechazos al 1% =", mean(pvalor < 0.01), "\n")
  cat("Proporción de rechazos al 5% =", mean(pvalor < 0.05), "\n")
  cat("Proporción de rechazos al 10% =", mean(pvalor < 0.1), "\n")
}
    ## 
## Proporción de rechazos al 1% = 0.008 
## Proporción de rechazos al 5% = 0.058 
## Proporción de rechazos al 10% = 0.106

    Análisis de los p-valores:

    hist(pvalor, freq=FALSE)
abline(h=1, lty=2)   # curve(dunif(x,0,1), add=TRUE)

    # Distribución empírica
curve(ecdf(pvalor)(x), type = "s", lwd = 2, 
      main = 'Tamaño del contraste', ylab = 'Proporción de rechazos', 
      xlab = 'Nivel de significación')
abline(a=0, b=1, lty=2)   # curve(punif(x, 0, 1), add = TRUE)

  5. Estudiar la potencia de los contrastes de los apartados c) y d), considerando como alternativa una distribución Weibull.

    La distribución exponencial es un caso particular de la Weibull: dexp(x, ratex) == dweibull(x, 1, 1/ratex). Estudiamos lo que ocurre al desplazar dweibull(x, shape, 1/ratex) con 0 < shape < 2.

    CUIDADO: las simulaciones pueden requerir de mucho tiempo de computación (consideramos valores pequeños de nx y nsim en datos y en ks.exp.sim).

    set.seed(54321)
nx <- 20
ratex <- 1    # Puede ser interesante representarlo variando rate
nsim <- 200
alfa <- 0.1   # Puede ser interesante representarlo variando alfa


shapex <- seq(0.25, 1.75, len=21)
preject <- numeric(length(shapex)) # Porporciones de rechazos con ks.test
ks.test.p <- function(x) ks.test(x, "pexp", 1/mean(x))$p.value
preject2 <- preject # Porporciones de rechazos con ks.exp.sim
ks.exp.sim.p <- function(x) ks.exp.sim(x, 200)$p.value

for (i in seq_along(shapex)) { 
  rx <- matrix(rweibull(nx*nsim, shape = shapex[i], scale = 1/ratex), ncol=nx)
  preject[i] <- mean( apply(rx, 1, ks.test.p) <= alfa )
  preject2[i] <- mean( apply(rx, 1, ks.exp.sim.p) <= alfa )
}

plot(shapex, preject, type="l", main = paste("Potencia del contraste ( alfa =", alfa, ")"), 
     xlab = "shape", ylab = "Proporción de rechazos")
lines(shapex, preject2, lty = 2)
abline(h = alfa, v = 1, lty = 3)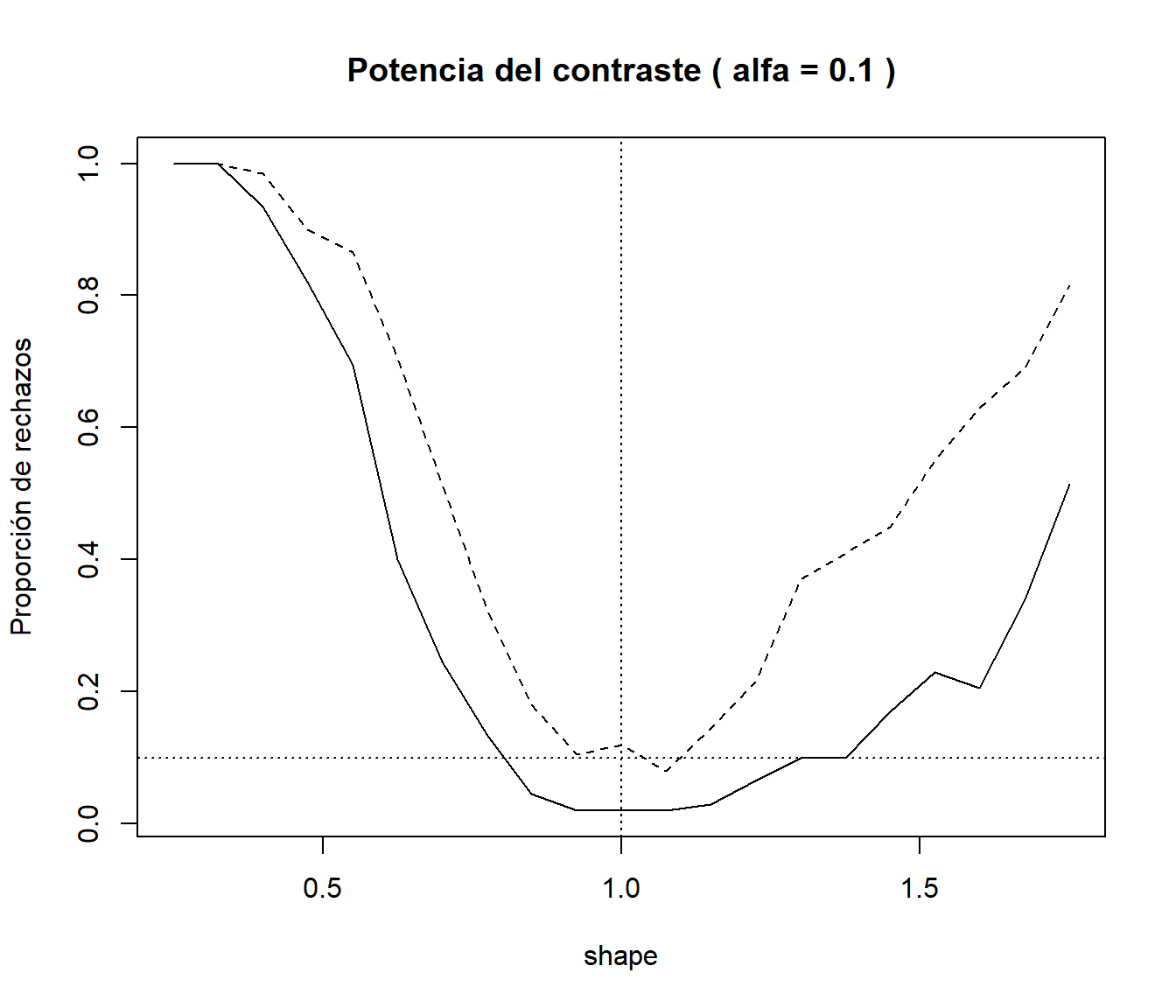

El estadístico de Kolmogorov-Smirnov Dn = max(c(DMinus, DPlus)) tiene ventajas desde el punto de vista teórico, pero puede no ser muy potente para detectar diferencias entre la distribución bajo la hipótesis nula y la distribución de los datos. La ventaja de la aproximación por simulación es que no estamos atados a resultados teóricos y podemos emplear el estadístico que se considere oportuno (la principal desventaja es el tiempo de computación). Por ejemplo, podríamos pensar en utilizar como estadístico la suma de los errores en valor absoluto del correspondiente gráfico PP, y solo habría que cambiar el estadístico Dn en la función ks.exp.sim por Dn = sum(abs( (1:n - 0.5)/n - pexp(sort(x), rate=rate) )).

7.4.4 Comparación de estimadores

Ejercicio 7.7 (Comparación de la eficiencia de la media muestral y de la mediana bajo contaminación)

Supongamos que estamos interesados en estudiar el efecto de datos atípicos en la estimación de la media teórica mediante la media y la mediana muestrales. Consideramos una variable aleatoria con distribución normal contaminada, en la que una observación procede de una \(N(0,1)\) con probabilidad 0.95 y de una \(N(3,3^2)\) con probabilidad 0.05 (mixtura). Se puede generar una muestra de esta variable (mixtura) mediante el método de composición descrito en la Sección 4.4, por ejemplo empleando el siguiente código:

p.sim <- rbinom(n, 1, 0.05)
dat.sim <- rnorm(n, 3*p.sim, 1+2*p.sim)

Podemos comparar la densidad objetivo con la de los valores contaminados:

curve(dnorm(x, 0, 1), -3, 12, ylab = 'densidad', lty = 3)
curve(0.95*dnorm(x, 0, 1) + 0.05*dnorm(x, 3, 3), add = TRUE)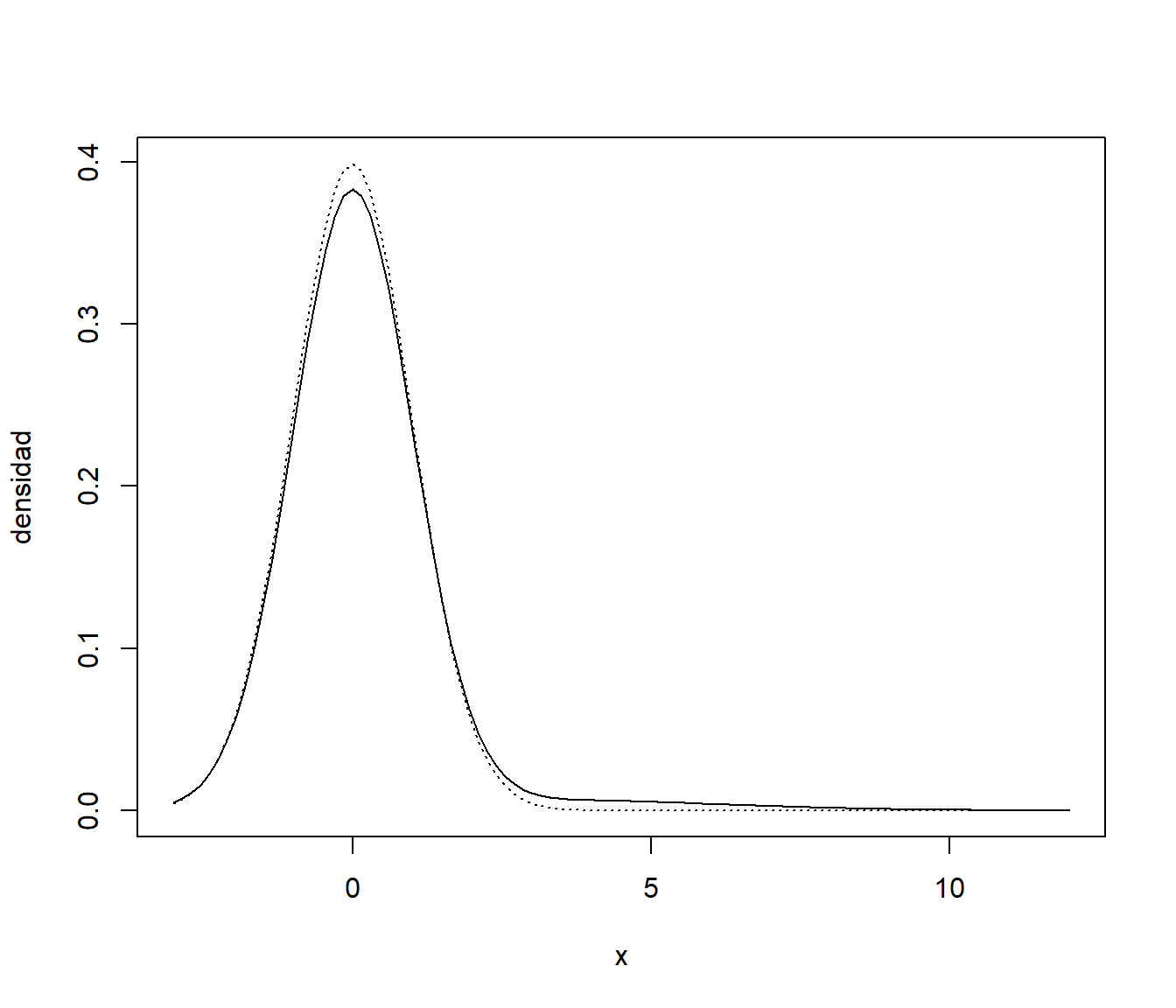

Nota:. Como se comentó en la Sección 4.4, también es habitual simular este tipo de datos generando un porcentaje alto de valores (en este caso un 95%) de la distribución base (\(N(0,1)\)) y el resto (5%) de la distibución “contaminadora” (\(N(3,3^2)\)), aunque se suele considerar un porcentaje de contaminación del 1% o inferior (además, como en este caso concreto no va importar el orden, no sería necesario combinar aleatoriamente los valores).


  1. Aproximar mediante simulación (500 generaciones) el sesgo y error estándar de la media y la mediana en el caso de una muestra de tamaño \(n=100\) (suponiendo que se pretende estimar la media no contaminada 0).

    # media y mediana
xsd <- 1
xmed <- 0
ndat <- 100
nsim <- 500

# for (isim in 1:nsim) # evitar matrix y apply
set.seed(1)
ntsim <- ndat*nsim
p.sim <- rbinom(ntsim, 1, 0.05)
dat.sim <- rnorm(ntsim, 3*p.sim, 1+2*p.sim)
dat.sim <- matrix(dat.sim, ncol=nsim)

    Cada columna es una muestra

    str(dat.sim[,1])
    ##  num [1:100] 0.197 -0.42 1.163 -0.406 0.744 ...
    hist(dat.sim[,1])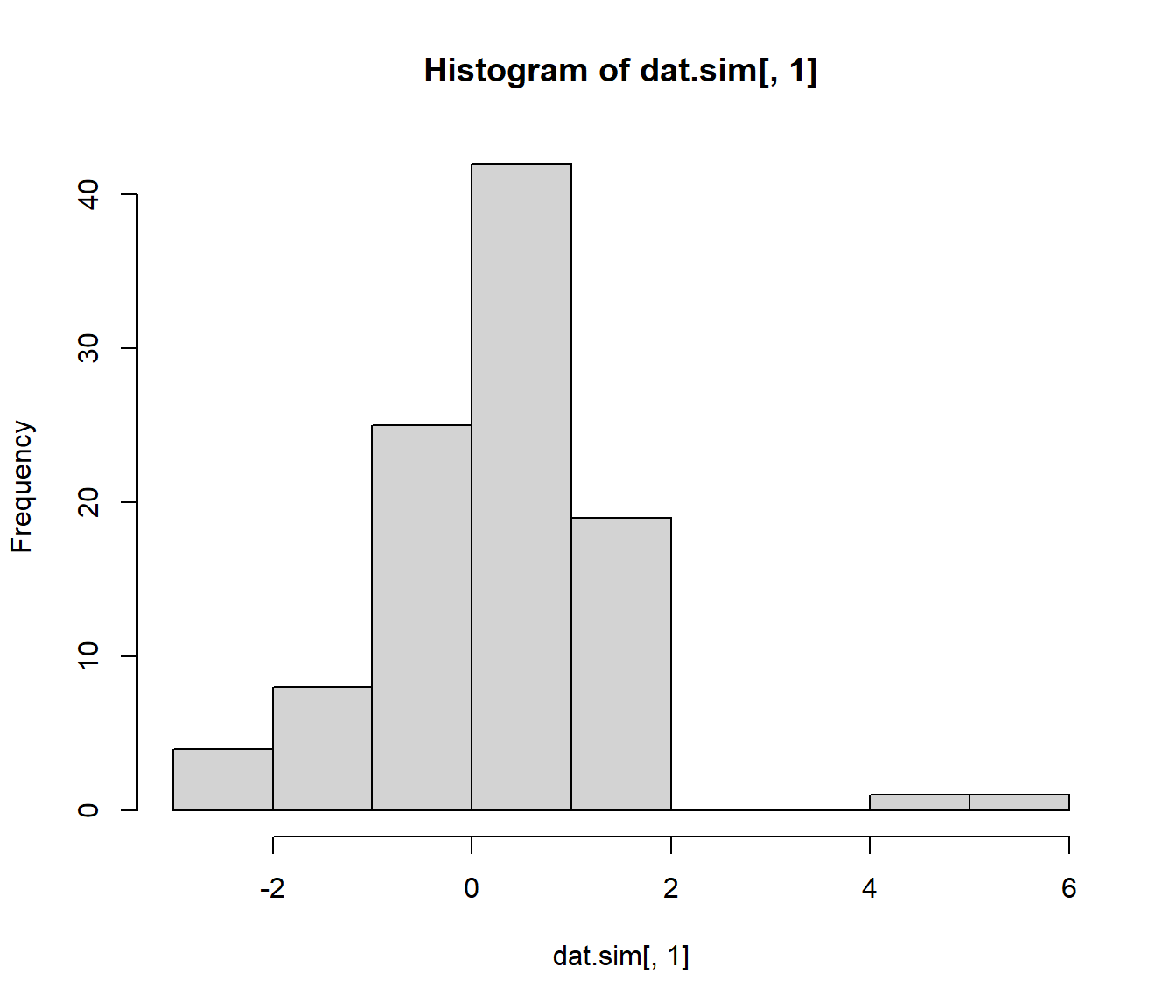

    Calculamos los estimadores:

    mean.sim <- apply(dat.sim, 2, mean)
median.sim <- apply(dat.sim, 2, median)

    Estimamos sus características:

    mean(mean.sim) # Coincide con el sesgo (media teórica es 0)
    ## [1] 0.1459986
    sd(mean.sim)
    ## [1] 0.1349537
    mean(median.sim) # Coincide con el sesgo (media teórica es 0)
    ## [1] 0.04453509
    sd(median.sim)
    ## [1] 0.1300611

    Sesgo:

    boxplot(mean.sim-xmed, median.sim-xmed, 
      names=c("Media","Mediana"), ylab="Sesgo")
abline(h = 0, lty = 2)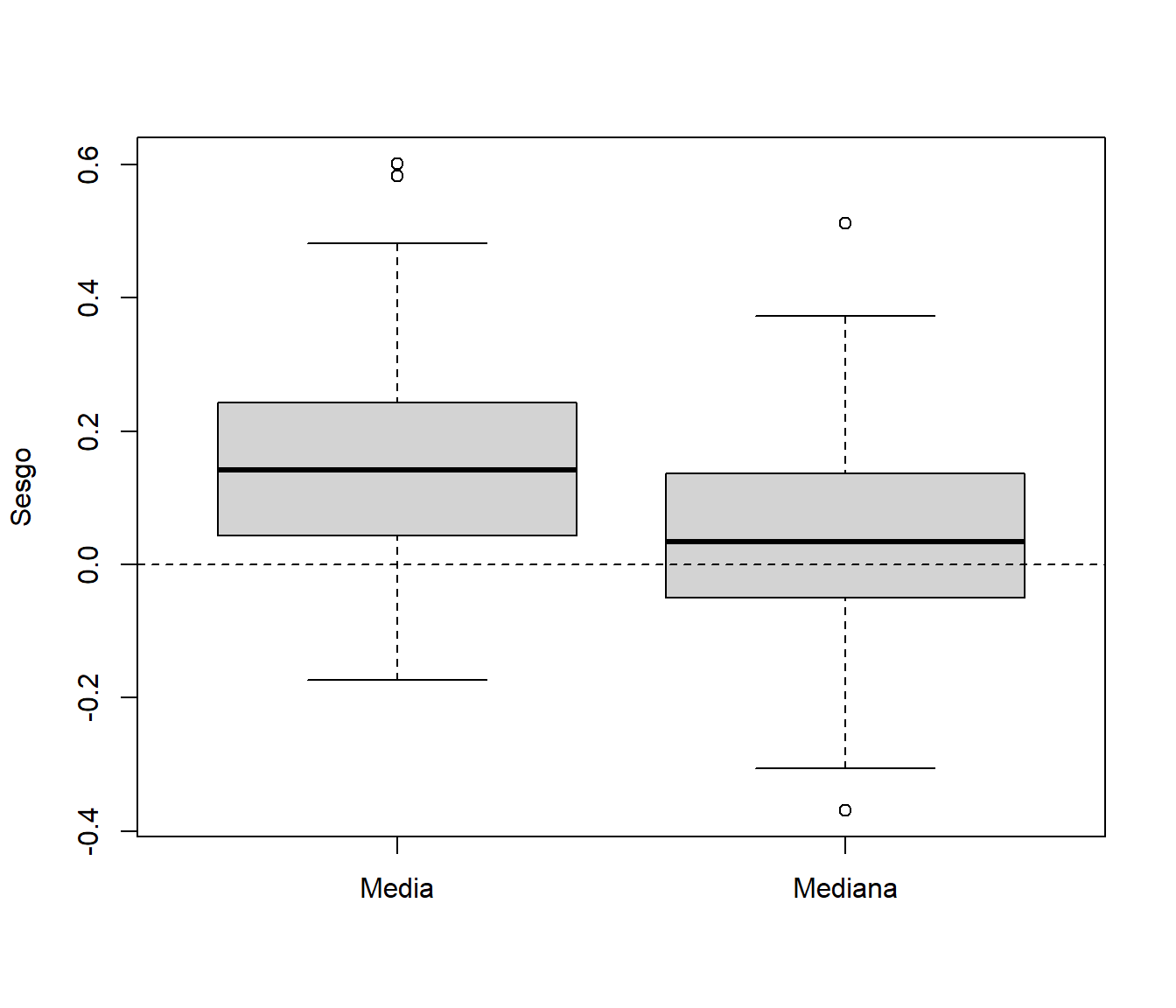

    Error cuadrático:

    boxplot((mean.sim-xmed)^2, (median.sim-xmed)^2, 
      names=c("Media","Mediana"), ylab="Error cuadrático")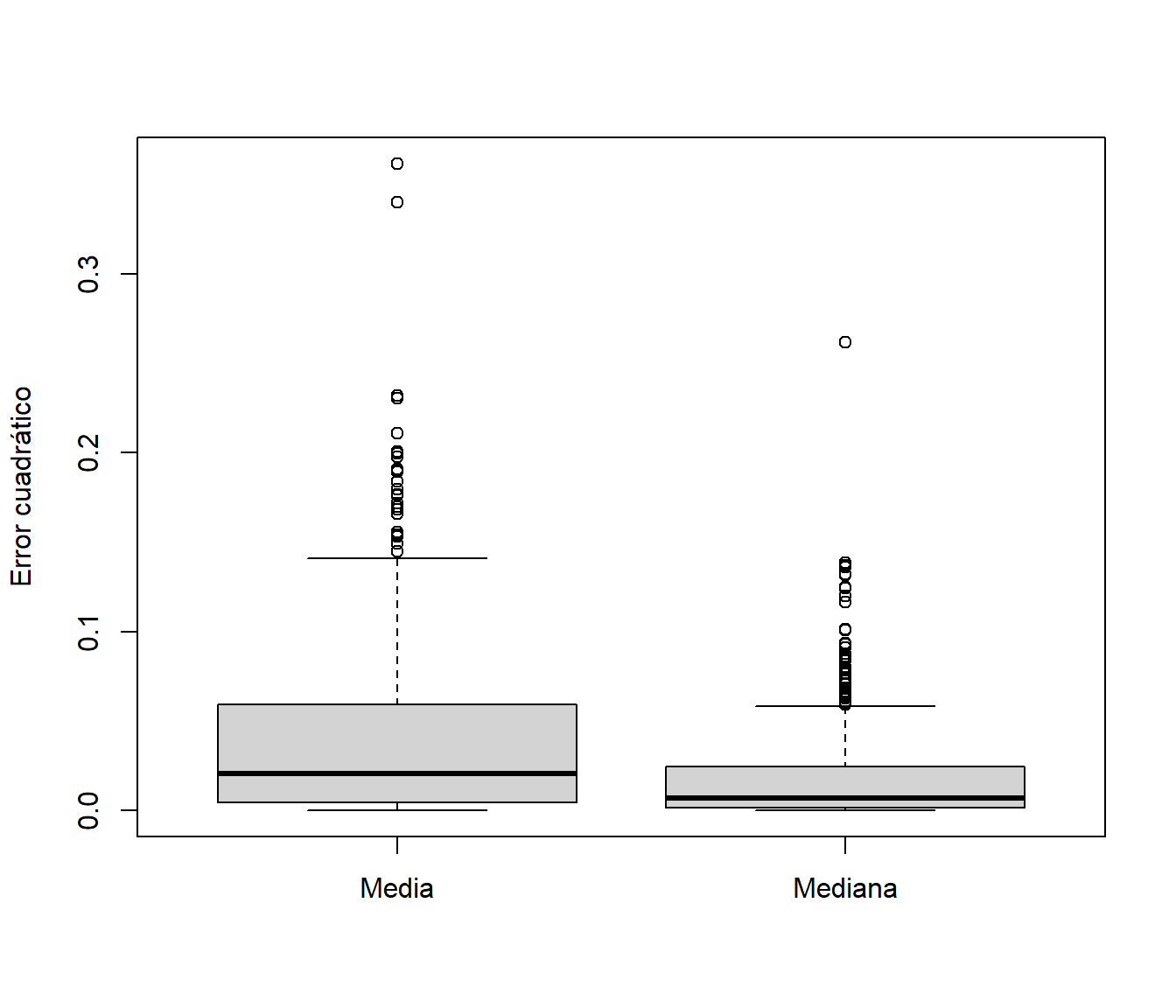

    Estadísticos error cuadrático:

    # SE media
summary((mean.sim-xmed)^2) 
    ##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000005 0.0045072 0.0206272 0.0394917 0.0591531 0.3619587
    # SE mediana
summary((median.sim-xmed)^2) 
    ##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000001 0.0016481 0.0070625 0.0188654 0.0243903 0.2618368