4.3 Modificaciones del método de aceptación-rechazo

En el tiempo de computación del algoritmo de aceptación-rechazo influye:

  • La proporción de aceptación (debería ser grande).

  • La dificultad de simular con la densidad auxiliar.

  • El tiempo necesario para hacer la comparación en el paso 3.

En ciertos casos el tiempo de computación necesario para evaluar \(f(x)\) puede ser alto. Para evitar evaluaciones de la densidad se puede emplear una función “squeeze” que aproxime la densidad por abajo (una envolvente inferior): \[s(x)\leq f(x) \text{, }\forall x\in \mathbb{R}.\]

Algoritmo 4.4 (Marsaglia, 1977)

  1. Generar \(U \sim \mathcal{U}(0, 1)\) y \(T\sim g\).

  2. Si \(c\cdot U\cdot g\left( T\right) \leq s\left( T\right)\) devolver \(X=T\),

    en caso contrario

    2.a. si \(c\cdot U\cdot g\left( T\right) \leq f\left( T\right)\) devolver \(X=T\),

    2.b. en caso contrario volver al paso 1.

Ilustración del algoritmo de aceptación-rechazo con envolvente inferior (función "squeeze").

Figura 4.12: Ilustración del algoritmo de aceptación-rechazo con envolvente inferior (función “squeeze”).

Cuanto mayor sea el área bajo \(s(x)\) (más próxima a 1) más efectivo será el algoritmo.

Se han desarrollado métodos generales para la construcción de las funciones \(g\) y \(s\) de forma automática (cada vez que se evalúa la densidad se mejoran las aproximaciones). Estos métodos se basan principalmente en que una transformación de la densidad objetivo es cóncava o convexa.

4.3.1 Muestreo por rechazo adaptativo (ARS)

Supongamos que \(f\) es una cuasi-densidad log-cóncava (i.e. \(\frac{\partial ^{2}}{\partial x^{2}}\log f(x) <0, ~\forall x\)).

Sea \(S_n=\left\{ x_{i}:i=0,\cdots ,n+1\right\}\) con \(f(x_{i})\) conocidos.

Denotamos por \(L_{i,i+1}(x)\) la recta pasando por \(\left( x_{i},\log f(x_{i})\right)\) y \(\left( x_{i+1},\log f(x_{i+1})\right)\)

  • \(L_{i,i+1}(x)\leq \log f(x)\) en el intervalo \(I_{i}=(x_{i},x_{i+1}]\)

  • \(L_{i,i+1}(x)\geq \log f(x)\) fuera de \(I_{i}\)

En el intervalo \(I_{i}\) se definen las envolventes de \(\log f\left( x\right)\):

  • \(\underline{\phi}_n(x)=L_{i,i+1}(x)\)

  • \(\overline{\phi}_n(x)=\min \left\{L_{i-1,i}(x),L_{i+1,i+2}(x)\right\}\)

Las envolventes de \(f(x)\) en \(I_{i}\) serán:

  • \(s_n(x)=\exp \left( \underline{\phi}_n(x)\right)\)

  • \(G_n(x)=\exp \left( \overline{\phi}_n(x)\right)\)

Tenemos entonces que: \[s_n(x)\leq f(x) \leq G_n(x)=c\cdot g_n(x)\] donde \(g_n(x)\) es una mixtura discreta de distribuciones tipo exponencial truncadas (las tasas pueden ser negativas), que se puede simular fácilmente combinando el método de composición (Sección 4.4) con el método de inversión.

Algoritmo 4.5 (Gilks, 1992)

  1. Inicializar \(n\) y \(s_n\).

  2. Generar \(U \sim \mathcal{U}(0, 1)\) y \(T\sim g_n\).

  3. Si \(U\cdot G_n\left( T\right) \leq s_n\left( T\right)\) devolver \(X=T\),

    en caso contrario,

    3.a Si \(U\cdot G_n\left( T\right) \leq f\left( T\right)\) devolver \(X=T\).

    3.b Hacer \(n=n+1\), añadir \(T\) a \(S_n\) y actualizar \(s_n\) y \(G_n\).

  4. Volver al paso 2.

Gilks y Wild (1992) propusieron una ligera modificación empleando tangentes para construir la cota superior, de esta forma se obtiene un método más eficiente pero requiere especificar la derivada de la densidad objetivo (ver Figura 4.12).

La mayoría de las densidades de la familia exponencial de distribuciones son log-cóncavas. Hörmann (1995) extendió esta aproximación al caso de densidades \(T_{c}\)-cóncavas: \[T_{c}(x) = signo(c)x^{c} \\ T_{0}(x) = \log (x).\] Aparte de la transformación logarítmica, la transformación \(T_{-1/2}(x)=-1/\sqrt{x}\) es habitualmente la más empleada.

4.3.2 Método del cociente de uniformes

Se puede ver como una modificación del método de aceptación-rechazo, de especial interés cuando el soporte no es acotado.

Si \((U,V)\) se distribuye uniformemente sobre: \[C_{f^{\ast}} = \left\{ (u, v) \in \mathbb{R}^{2} : 0<u\leq \sqrt{f^{\ast}(v/u)} \right\},\] siendo \(f^{\ast}\) una función no negativa integrable (cuasi-densidad), entonces \(X=V/U\) tiene función de densidad proporcional a \(f^{\ast}\) (Kinderman y Monahan, 1977). Además \(C_{f^{\ast}}\) tiene área finita, por lo que pueden generarse fácilmente los valores \((U,V)\) con distribución \(\mathcal{U}\left(C_{f^{\ast}}\right)\) a partir de componentes uniformes unidimensionales (aceptando los puntos dentro de \(C_{f^{\ast}}\)).

De modo análogo al método de aceptación-rechazo, hay modificaciones para acelerar los cálculos y automatizar el proceso, construyendo regiones mediante polígonos: \[C_{i}\subset C_{f^{\ast}}\subset C_{s}.\] También se puede extender al caso multivariante y considerar transformaciones adicionales. Ver por ejemplo el paquete rust.

Ejemplo 4.5 (simulación de la distribución de Cauchy mediante cociente de uniformes)

Si consideramos la distribución de Cauchy: \[f(x) = \frac{1}{\pi (1 + x^2)} \text{, } x\in \mathbb{R},\] eliminando la constante por comodidad \(f(x) \propto 1/(1 + x^2)\), se tiene que: \[\begin{aligned} C_{f^{\ast}} & = \left\{ (u, v) \in \mathbb{R}^{2} : 0 <u \leq \frac{1}{\sqrt{1 + (v/u)^2}} \right\} \\ & = \left\{ (u, v) \in \mathbb{R}^{2} : u > 0, u^2 \leq \frac{u^2}{u^2 + v^2} \right\} \\ & = \left\{ (u, v) \in \mathbb{R}^{2} : u > 0, u^2 + v^2 \leq 1 \right\}, \end{aligned}\] dando como resultando que \(C_{f^{\ast}}\) es el semicírculo de radio uno, y podemos generar valores con distribución uniforme en esta región a partir de \(\mathcal{U}\left([0,1]\times[-1,1] \right)\).

El correspondiente algoritmo está implementado en la función rcauchy.rou() del paquete simres (fichero ar.R):

simres::rcauchy.rou
## function(n) {
##   # Cauchy mediante cociente de uniformes
##   ngen <- n
##   u <- runif(n, 0, 1)
##   v <- runif(n, -1, 1)
##   x <- v/u
##   ind <- u^2 + v^2 > 1 # TRUE si no verifica condición
##   # Volver a generar si no verifica condición
##   while (le <- sum(ind)){ # mientras le = sum(ind) > 0
##     ngen <- ngen + le
##     u <- runif(le, 0, 1)
##     v <- runif(le, -1, 1)
##     x[ind] <- v/u
##     ind[ind] <- u^2 + v^2 > 1 # TRUE si no verifica condición
##   }
##   attr(x, "ngen") <- ngen
##   return(x)
## }
## <bytecode: 0x000001a317f07928>
## <environment: namespace:simres>
set.seed(1)
nsim <- 10^4
rx <- simres::rcauchy.rou(nsim)

hist(rx, breaks = "FD", freq = FALSE, main = "", xlim = c(-6, 6))
curve(dcauchy, add = TRUE)
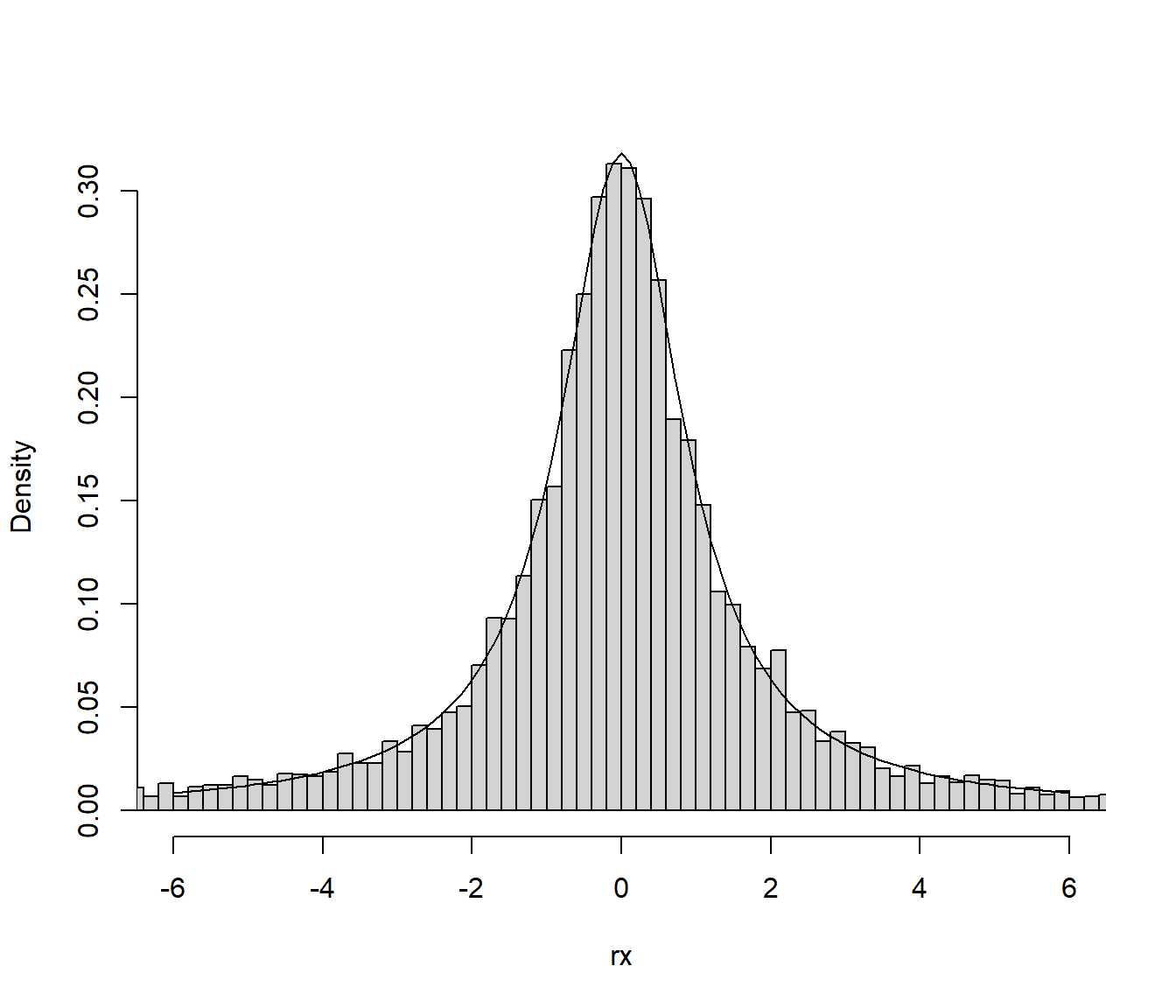
Distribución de los valores generados mediante el método de cociente de uniformes.

Figura 4.13: Distribución de los valores generados mediante el método de cociente de uniformes. 

# Número generaciones
ngen <- attr(rx, "ngen")
{cat("Número de generaciones = ", ngen)
cat("\nNúmero medio de generaciones = ", ngen/nsim)
cat("\nProporción de rechazos = ", 1-nsim/ngen,"\n")}
## Número de generaciones =  12751
## Número medio de generaciones =  1.2751
## Proporción de rechazos =  0.2157478