4.1 Método de inversión

En general sería el método preferible para la simulación de una variable continua (siempre que se disponga de la función cuantil). Está basado en los siguientes resultados:

Si \(X\) es una variable aleatoria con función de distribución \(F\) continua y estrictamente monótona (invertible), entonces: \[U = F\left( X \right) \sim \mathcal{U}(0, 1)\] ya que: \[G\left( u \right) = P\left( Y \leq u \right) = P\left( F(X) \leq u \right) \\ = P\left( X \leq F^{-1}(u) \right) = F\left( F^{-1}(u) \right) = u\]

El recíproco también es cierto, si \(U \sim \mathcal{U}(0, 1)\) entonces: \[F^{-1}\left( U \right) \sim X\]

A partir de este resultado se deduce el siguiente algoritmo genérico para simular una variable continua con función de distribución \(F\) invertible:

Algoritmo 4.1 (Método de inversión)

  1. Generar \(U \sim \mathcal{U}(0, 1)\).

  2. Devolver \(X = F^{-1}\left( U \right)\).

Ejemplo 4.1 (simulación de una distribución exponencial)

La distribución exponencial \(\exp \left( \lambda \right)\) de parámetro \(\lambda>0\) tiene como función de densidad \(f(x) =\lambda e^{-\lambda x}\), si \(x\geq 0\), y como función de distribución: \[F(x)=\left\{ \begin{array}{ll} 1-e^{-\lambda x} & \text{si } x \ge 0 \\ 0 & \text{si } x < 0\\ \end{array} \right.\]

Teniendo en cuenta que: \[1-e^{-\lambda x}=u \Leftrightarrow x=-\frac{\ln \left( 1-u\right) }{ \lambda }\] el algoritmo para simular esta variable mediante el método de inversión es:

  1. Generar \(U \sim \mathcal{U}(0, 1)\).

  2. Devolver \(X=-\dfrac{\ln \left( 1-U\right) }{\lambda }\).

En el último paso podemos emplear directamente \(U\) en lugar de \(1-U\), ya que \(1 - U \sim \mathcal{U}(0, 1)\). Esta última expresión para acelerar los cálculos es la que denominaremos forma simplificada.

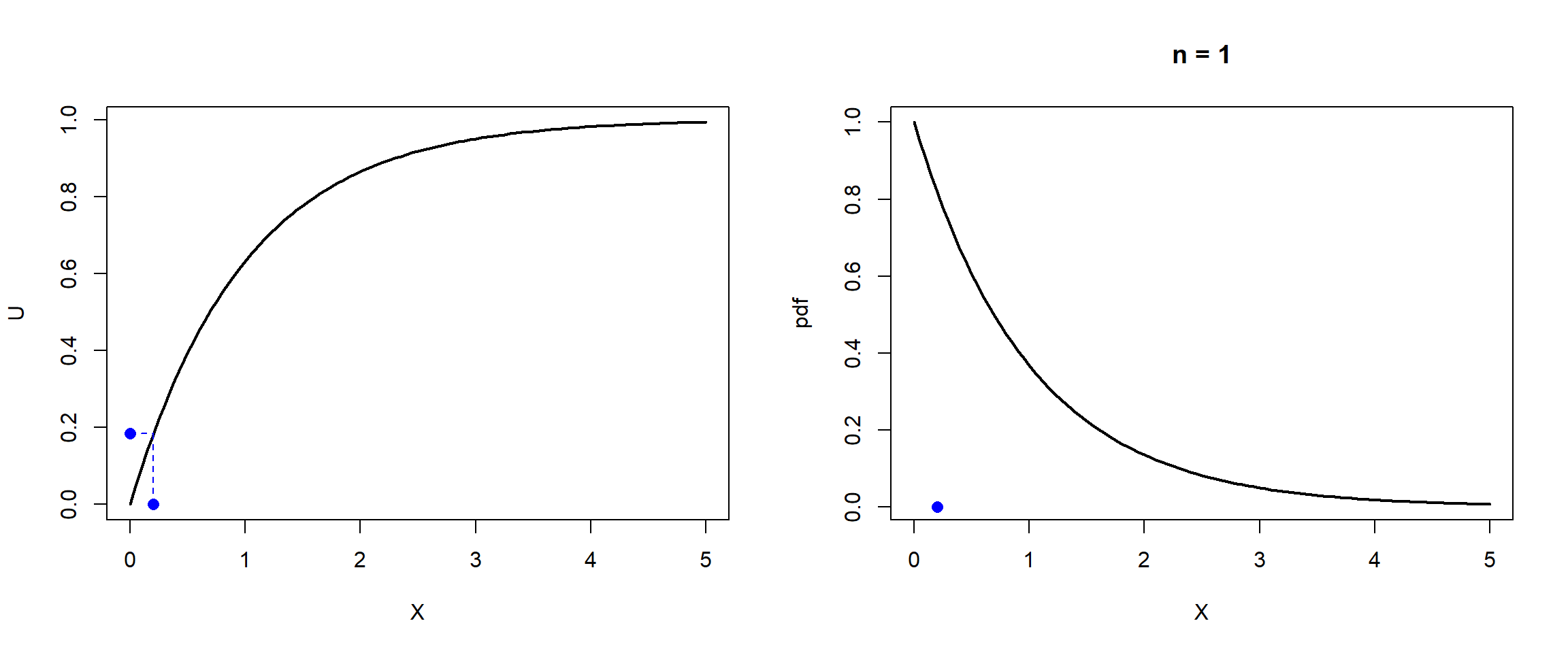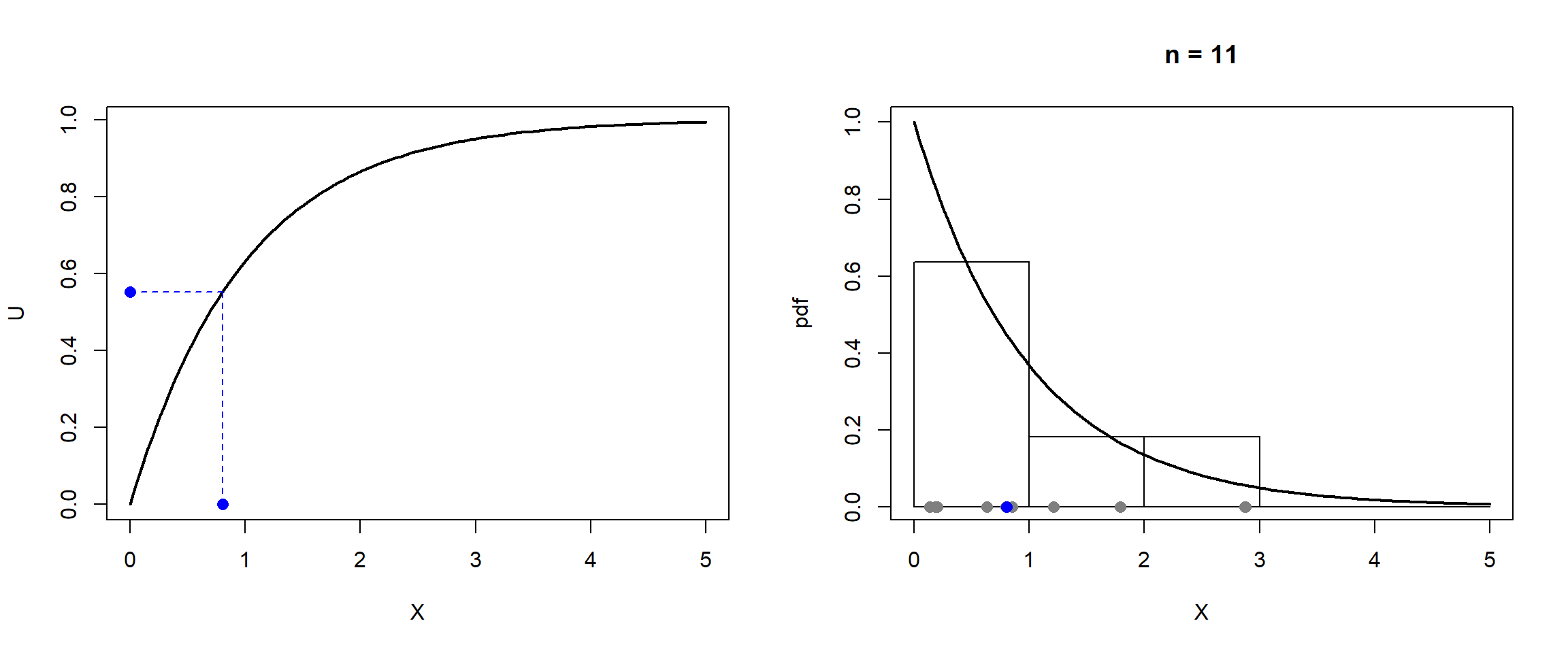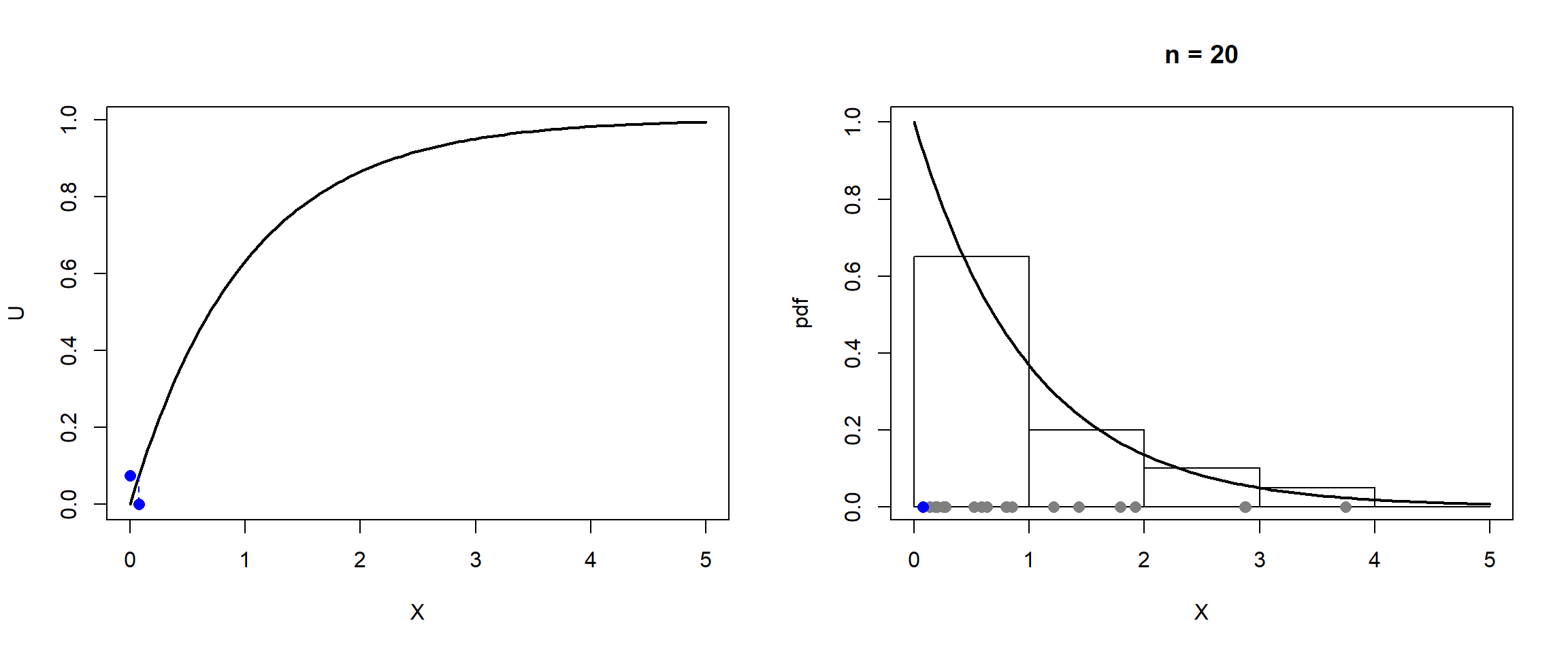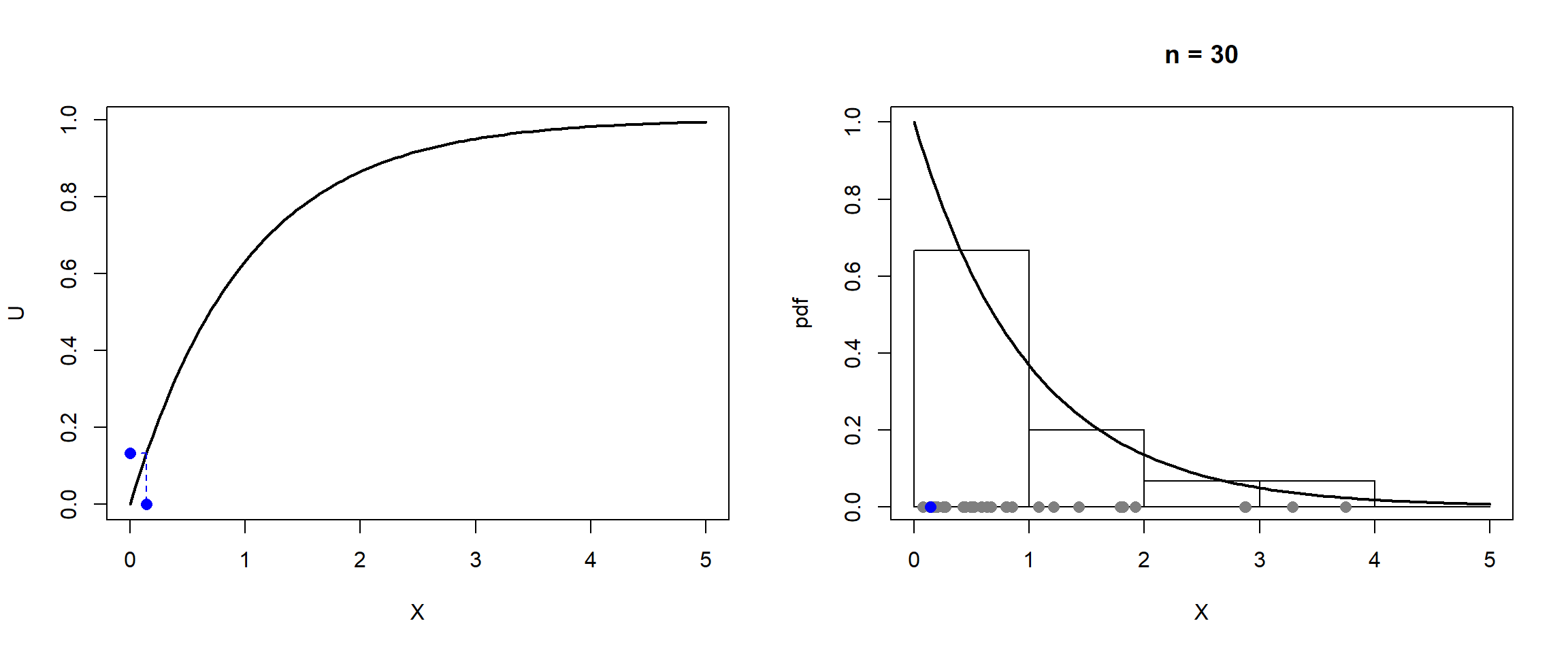
Ilustración de la simulación de una distribución exponencial por el método de inversión.

Figura 4.1: Ilustración de la simulación de una distribución exponencial por el método de inversión.

El código para implementar este algoritmo en R podría ser el siguiente:

tini <- proc.time()

lambda <- 2
nsim <- 10^5
set.seed(1)
u <- runif(nsim)
x <- -log(u)/lambda # -log(1-u)/lambda

tiempo <- proc.time() - tini
tiempo
##    user  system elapsed 
##       0       0       0
hist(x, breaks = "FD", freq = FALSE, 
        main = "", xlim = c(0, 5), ylim = c(0, 2.5))
curve(dexp(x, lambda), lwd = 2, add = TRUE)
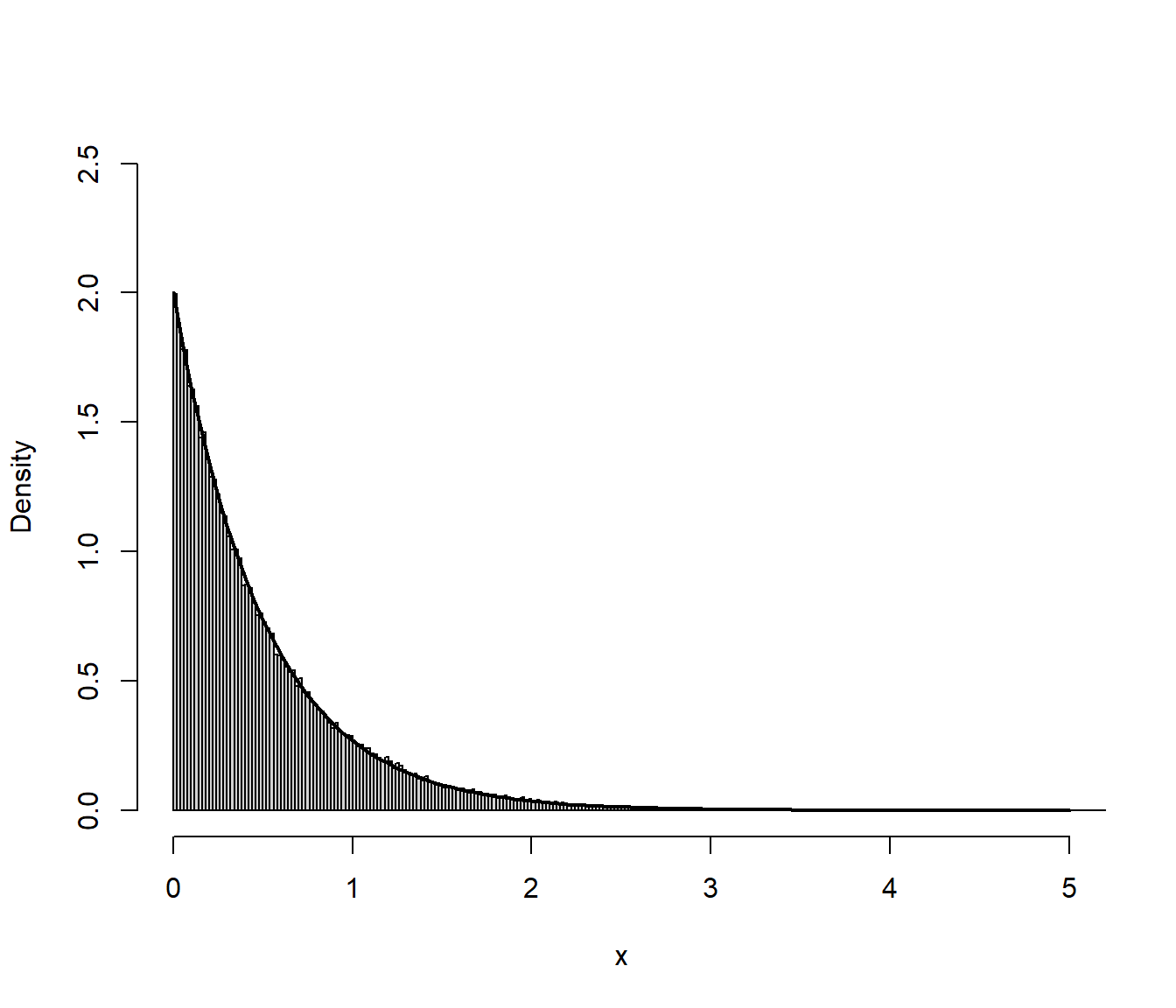
Distribución de los valores generados de una exponencial mediante el método de inversión.

Figura 4.2: Distribución de los valores generados de una exponencial mediante el método de inversión.

Como se observa en la Figura 4.2 se trata de un método exacto (si está bien implementado) y la distribución de los valores generados se aproxima a la distribución teórica como cabría esperar con una muestra de ese tamaño.

4.1.1 Algunas distribuciones que pueden simularse por el método de inversión

A continuación se incluyen algunas distribuciones que se pueden simular fácilmente mediante el método de inversión. Se adjunta una forma simplificada del método que tiene por objeto evitar cálculos innecesarios (tal y como se hizo en el ejemplo de la exponencial).

Nombre Densidad \(F(x)\) \(F^{-1}\left( U\right)\) Forma simplificada
\(\exp\left( \lambda\right)\) (\(\lambda>0\)) \(\lambda e^{-\lambda x}\), si \(x\geq0\) \(1-e^{-\lambda x}\) \(-\dfrac{\ln\left( 1-U\right) }\lambda\) \(-\dfrac{\ln U}\lambda\)
Cauchy \(\dfrac1{\pi\left( 1+x^{2}\right)}\) \(\dfrac12+\dfrac{\arctan x}\pi\) \(\tan\left( \pi\left( U-\dfrac12\right) \right)\) \(\tan\pi U\)
Triangular en \(\left( 0,a\right)\) \(\dfrac2a\left( 1-\dfrac xa\right)\), si \(0\leq x\leq a\) \(\dfrac2a\left(x-\dfrac{x^{2}}{2a}\right)\) \(a\left( 1-\sqrt{1-U}\right)\) \(a\left( 1-\sqrt{U}\right)\)
Pareto (\(a,b>0\)) \(\dfrac{ab^{a}}{x^{a+1}}\), si \(x\geq b\) \(1-\left( \dfrac bx\right)^{a}\) \(\dfrac b{\left( 1-U\right)^{1/a}}\) \(\dfrac b{U^{1/a}}\)
Weibull (\(\lambda,\alpha>0\)) \(\alpha\lambda^{\alpha}x^{\alpha-1}e^{-\left( \lambda x\right) ^{\alpha}}\), si \(x\geq0\) \(1-e^{-\left( \lambda x\right)^{\alpha}}\) \(\dfrac{\left( -\ln\left(1-U\right) \right)^{1/\alpha}}\lambda\) \(\dfrac{\left( -\ln U\right)^{1/\alpha}}\lambda\)

Ejercicio 4.1 (distribución doble exponencial)

La distribución doble exponencial12 (o distribución de Laplace) de parámetro \(\lambda\) tiene función de densidad: \[f(x) =\frac{\lambda}{2}e^{-\lambda\left\vert x\right\vert }\text{, }x\in\mathbb{R}\]

y función de distribución:

\[F(x) =\int_{-\infty}^{x}f\left( t\right) dt=\left\{ \begin{array}{ll} \frac{1}{2}e^{\lambda x} & \text{si } x<0\\ 1-\frac{1}{2}e^{-\lambda x} & \text{si } x\geq0 \end{array} \ \right.\]

  1. Escribir una función que permita generar, por el método de inversión, una muestra de \(n\) observaciones de esta distribución.

    ddexp <- function(x, lambda = 1){
# Densidad doble exponencial
  lambda*exp(-lambda*abs(x))/2
}

rdexp <- function(lambda = 1){
# Simulación por inversión
# Doble exponencial
  u <- runif(1)
  if (u<0.5) {
    return(log(2*u)/lambda)
  } else {
    return(-log(2*(1-u))/lambda)
  }
}

rdexpn <- function(n = 1000, lambda = 1) {
# Simulación n valores de doble exponencial
    x <- numeric(n)
    for(i in 1:n) x[i]<-rdexp(lambda)
    return(x)
}

  2. Generar \(10^{4}\) valores de la distribución doble exponencial de parámetro \(\lambda=2\) y obtener el tiempo de CPU que tarda en generar la secuencia.

    set.seed(54321)
system.time(x <- rdexpn(10^4, 2))
    ##    user  system elapsed 
##    0.01    0.00    0.01

  3. Representar el histograma y compararlo con la densidad teórica.

    hist(x, breaks = "FD", freq = FALSE, main="")
# lines(density(x), col = 'blue')
curve(ddexp(x, 2), add = TRUE)
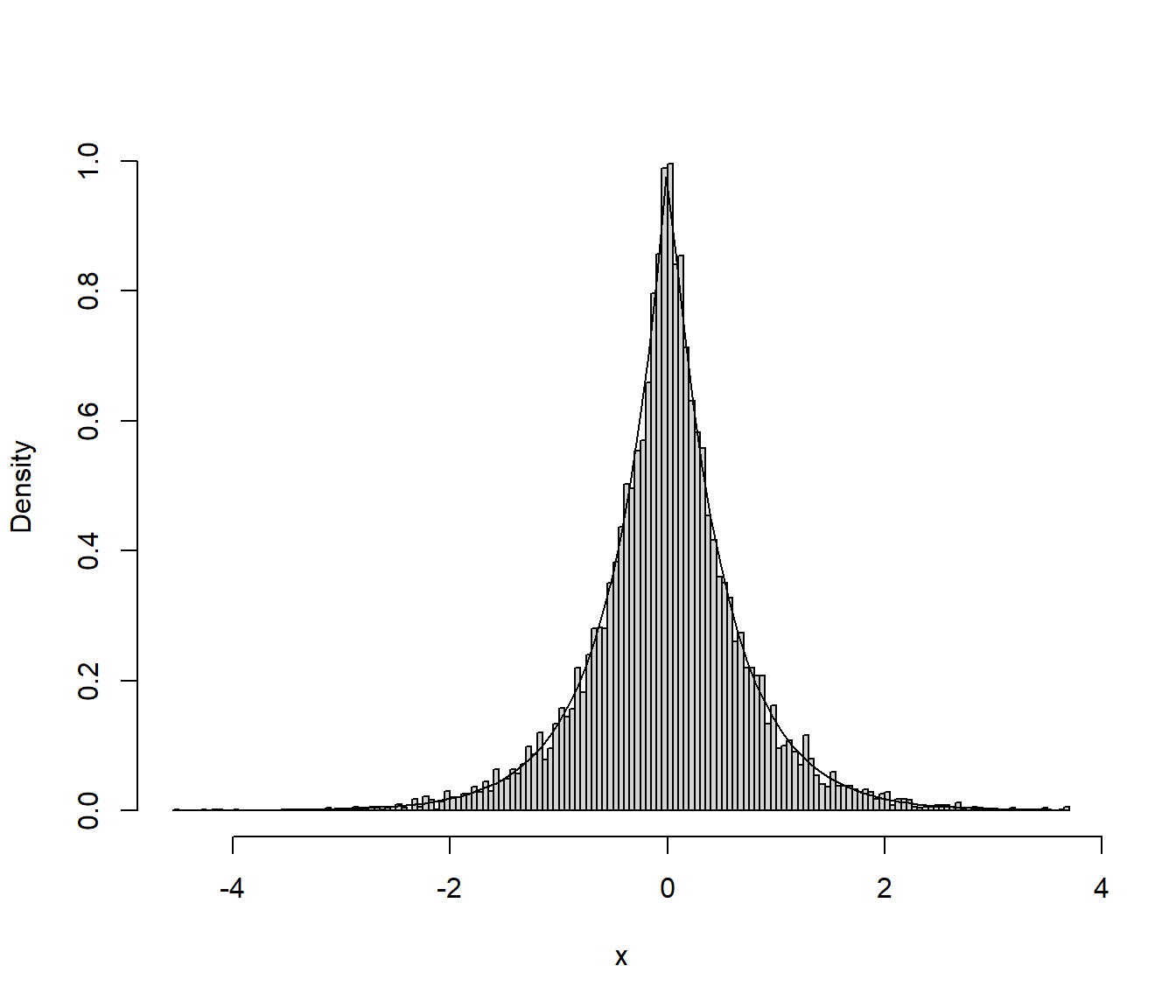
    Distribución de los valores generados de una doble exponencial mediante el método de inversión.

    Figura 4.3: Distribución de los valores generados de una doble exponencial mediante el método de inversión.

    Como se trata de un método exacto de simulación, si está bien implementado, la distribución de los valores generados debería comportarse como una muestra genuina de la distribución objetivo.

4.1.2 Ventajas e inconvenientes

La principal ventaja de este método es que, en general, sería aplicable a cualquier distribución continua (como se muestra en la Sección 5.1, se puede extender al caso de que la función de distribución no sea invertible, incluyendo distribuciones discretas).

Uno de los principales problemas es que puede no ser posible encontrar una expresión explícita para \(F^{-1}\left( u\right)\) (en ocasiones, como en el caso de la distribución normal, ni siquiera se dispone de una expresión explícita para la función de distribución). Además, aún disponiendo de una expresión explícita para \(F^{-1}\left( u\right)\), su evaluación directa puede requerir de mucho tiempo de computación.

Como alternativa a estos inconvenientes se podrían emplear métodos numéricos para resolver \(F(x) - u = 0\) de forma aproximada, aunque habría que resolver numéricamente esta ecuación para cada valor aleatorio que se desea generar. Otra posibilidad, en principio preferible, sería emplear una aproximación a \(F^{-1}\left( u\right)\), dando lugar al método de inversión aproximada (como se indicó en la Sección 1.3.1, R emplea por defecto este método para la generación de la distribución normal).

4.1.3 Inversión aproximada

En muchos casos en los que no se puede emplear la expresión exacta de la función cuantil \(F^{-1}\left( u\right)\), se dispone de una aproximación suficientemente buena que se puede emplear en el algoritmo anterior (se obtendrían simulaciones con una distribución aproximada a la deseada).

Por ejemplo, para aproximar la función cuantil de la normal estándar, Odeh y Evans (1974) consideraron la siguiente función auxiliar13: \[ g\left( v\right) =\sqrt{-2\ln v}\frac{A\left( \sqrt{-2\ln v}\right) }{B\left( \sqrt{-2\ln v}\right) },\] siendo \(A(x) =\sum_{i=0}^{4}a_{i}x^{i}\) y \(B(x) =\sum_{i=0}^{4}b_{i}x^{i}\) con:

\[\begin{array}{ll} a_{0}=-0.322232431088 & b_{0}=0.0993484626060 \\ a_{1}=-1 & b_{1}=0.588581570495 \\ a_{2}=-0.342242088547 & b_{2}=0.531103462366 \\ a_{3}=-0.0204231210245 & b_{3}=0.103537752850 \\ a_{4}=-0.0000453642210148 & b_{4}=0.0038560700634 \end{array}\]

La aproximación consiste en utilizar \(g\left( 1-u\right)\) en lugar de \(F^{-1}\left( u\right)\) para los valores de \(u\in[10^{-20},\frac12]\) y \(-g\left( u\right)\) si \(u\in[\frac12,1-10^{-20}]\). Para \(u\notin [10^{-20},1-10^{-20}]\) (que sólo ocurre con una probabilidad de \(2\cdot10^{-20}\)) la aproximación no es recomendable.

Algoritmo 4.2 (de Odeh y Evans)

  1. Generar \(U \sim U(0, 1)\).

  2. Si \(U<10^{-20}\) ó \(U>1-10^{-20}\) entonces volver a 1.

  3. Si \(U<0.5\) entonces hacer \(X=g\left(1-U\right)\) en caso contrario hacer \(X=-g\left( U\right)\).

  4. Devolver \(X\).

En manuales de funciones matemáticas, como Abramowitz y Stegun (1964), se tienen aproximaciones de la función cuantil de las principales distribuciones (por ejemplo en la página 993 las correspondientes a la normal estándar).

  1. Esta distribución también se puede generar fácilmente simulando una distribución exponencial y asignando un signo positivo o negativo con equiprobabilidad (ver Ejemplo 4.6) y función simres::rdexp() (fichero ddexp.R).↩︎

  2. R emplea una aproximación similar, basada en el algoritmo de Wichura (1988) más preciso, y que está implementado en el fichero fuente qnorm.c.↩︎