1.2 Tipos de números aleatorios

El primer requisito para poder realizar simulación estocástica sería disponer de números aleatorios. Se distingue entre tres tipos de secuencias:

  • números aleatorios puros (true random): se caracteriza porque no existe ninguna regla o plan que nos permita conocer sus valores.

  • números pseudo-aleatorios: simulan realizaciones de una variable aleatoria (uniforme),

  • números cuasi-aleatorios: secuencias deterministas con una distribución más regular en el rango considerado.

1.2.1 Números aleatorios puros

Normalmente son obtenidos por procesos físicos (loterías, ruletas, ruidos…) y, hasta hace una décadas, se almacenaban en tablas de dígitos aleatorios. Por ejemplo, en 1955 la Corporación RAND publicó el libro A Million Random Digits with 100,000 Normal Deviates que contenía números aleatorios generados mediante una ruleta electrónica conectada a una computadora (ver Figura 1.4).

Líneas 10580-10594, columnas 21-40, del libro *A Million Random Digits with 100,000 Normal Deviates*.

Figura 1.4: Líneas 10580-10594, columnas 21-40, del libro A Million Random Digits with 100,000 Normal Deviates.

El procedimiento que se utilizaba para seleccionar de una tabla, de forma manual, números aleatorios en un rango de 1 a m era el siguiente:

  • Se selecciona al azar un punto de inicio en la tabla y la dirección que se seguirá.

  • Se agrupan los dígitos de forma que “cubran” el valor de m.

  • Se va avanzado en la dirección elegida, seleccionando los valores menores o iguales que m y descartando el resto.

Hoy en día están disponibles generadores de números aleatorios “online”, por ejemplo:

  • RANDOM.ORG: ruido atmosférico (ver paquete random en R).

  • HotBits: desintegración radiactiva.

Aunque para un uso profesional es recomendable emplear generadores implementados mediante hardware:

Sus principales aplicaciones hoy en día son en criptografía y juegos de azar, donde resulta especialmente importante su impredecibilidad.

El uso de números aleatorios puros presenta dos grandes incovenientes. El principal para su aplicación en el campo de la Estadística (y en otros casos) es que los valores generados deberían ser independientes e idénticamente distribuidos con distribución conocida, algo que resulta difícil (o imposible) de garantizar. Siempre está presente la posible aparición de sesgos, principalmente debidos a fallos del sistema o interferencias. Por ejemplo, en el caso de la máquina RAND, fallos mecánicos en el sistema de grabación de los datos causaron problemas de aleatoriedad (Hacking, 1965, p. 129).

El otro inconveniente estaría relacionado con su reproducibilidad, por lo que habría que almacenarlos en tablas si se quieren volver a reproducir los resultados. A partir de la década de 1960, al disponer de computadoras de mayor velocidad, empezó a resultar más eficiente generar valores mediante software en lugar de leerlos de tablas.

1.2.2 Números cuasi-aleatorios

Algunos problemas, como la integración numérica (en el Capítulo 7 se tratarán métodos de integración Monte Carlo), no dependen realmente de la aleatoriedad de la secuencia. Para evitar generaciones poco probables, se puede recurrir a secuencias cuasi-aleatorias, también denominadas sucesiones de baja discrepancia (hablaríamos entonces de métodos cuasi-Monte Carlo). La idea sería que la proporción de valores en una región cualquiera sea siempre aproximadamente proporcional a la medida de la región (como sucedería en media con la distribución uniforme, aunque no necesariamente para una realización concreta).

Por ejemplo, el paquete randtoolbox de R implementa métodos para la generación de secuencias cuasi-aleatorias (ver Figura 1.5).

library(randtoolbox)
n <- 2000
par.old <- par(mfrow = c(1, 3))
plot(halton(n, dim = 2), xlab = 'x1', ylab = 'x2')
plot(sobol(n, dim = 2), xlab = 'x1', ylab = 'x2')
plot(torus(n, dim = 2), xlab = 'x1', ylab = 'x2')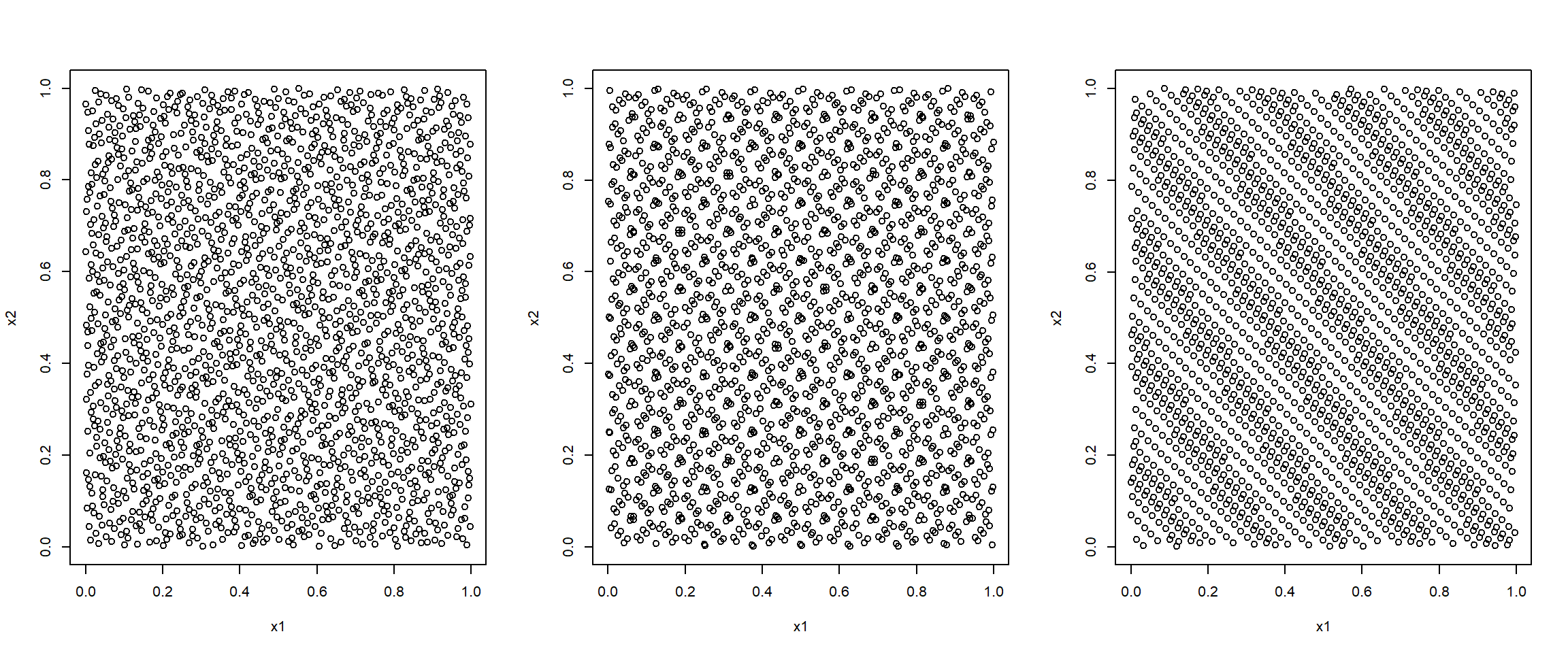
Secuencias cuasi-aleatorias bidimensionales obtenidas con los métodos de Halton (izquierda), Sobol (centro) y Torus (derecha).

Figura 1.5: Secuencias cuasi-aleatorias bidimensionales obtenidas con los métodos de Halton (izquierda), Sobol (centro) y Torus (derecha). 

par(par.old)

En este libro sólo consideraremos los números pseudoaleatorios y por comodidad se eliminará el prefijo “pseudo” en algunos casos.

1.2.3 Números pseudo-aleatorios

La mayoría de los métodos de simulación se basan en la posibilidad de generar números pseudoaleatorios que imiten las propiedades de valores independientes de la distribución \(\mathcal{U}(0,1)\), es decir, que imiten las propiedades de una muestra aleatoria simple3 de esta distribución.

El procedimiento habitual para obtener estas secuencias es emplear un algoritmo recursivo denominado generador:

\[x_{i} = f\left( x_{i-1}, x_{i-2}, \cdots, x_{i-k}\right)\]

donde:

  • \(k\) es el orden del generador.

  • \(\left( x_{0},x_{1},\cdots,x_{k-1}\right)\) es la semilla (estado inicial).

El periodo o longitud del ciclo es la longitud de la secuencia antes de que vuelva a repetirse. Lo denotaremos por \(p\).

Los números de la sucesión son predecibles, conociendo el algoritmo y la semilla. Sin embargo, si no se conociesen, no se debería poder distinguir una serie de números pseudoaleatorios de una sucesión de números verdaderamente aleatoria (utilizando recursos computacionales razonables). En caso contrario esta predecibilidad puede dar lugar a serios problemas (e.g. http://eprint.iacr.org/2007/419).

Como regla general, por lo menos mientras se está desarrollando un programa, interesa fijar la semilla de aleatorización.

  • Permite la reproducibilidad de los resultados.

  • Facilita la depuración del código.

Todo generador de números pseudoaleatorios mínimamente aceptable debe comportarse como si proporcionase muestras genuinas de datos independientes de una \(\mathcal{U}(0,1)\). Otras propiedades de interés son:

  • Reproducibilidad a partir de la semilla.

  • Periodo suficientemente largo.

  • Eficiencia (rapidez y requerimientos de memoria).

  • Portabilidad.

  • Generación de sub-secuencias (computación en paralelo).

  • Parsimonia.

Es importante asegurarse de que el generador empleado es adecuado:

“Random numbers should not be generated with a method chosen at random.”

— Knuth, D.E. (TAOCP, 2002)

Se dispone de una gran cantidad de algoritmos. Los primeros intentos (cuadrados medios, método de Lehmer…) resultaron infructuosos, pero al poco tiempo ya se propusieron métodos que podían ser ampliamente utilizados (estableciendo adecuadamente sus parámetros). Entre ellas podríamos destacar:

  • Generadores congruenciales.

  • Registros desfasados.

  • Combinaciones de distintos algoritmos.

La recomendación sería emplear un algoritmo conocido y que haya sido estudiado en profundidad (por ejemplo el generador Mersenne-Twister empleado por defecto en R, propuesto por Matsumoto y Nishimura, 1998). Además, sería recomendable utilizar alguna de las implementaciones disponibles en múltiples librerías, por ejemplo:

En este libro nos centraremos en los generadores congruenciales, descritos en la Sección 2.1. Estos métodos son muy simples, aunque con las opciones adecuadas podrían ser utilizados en pequeños estudios de simulación. Sin embargo, su principal interés es que constituyen la base de los generadores avanzados habitualmente considerados.

  1. Aunque hay que distinguir entre secuencia y muestra. En un problema de inferencia, en principio estamos interesados en una característica desconocida de la población. En cambio, en un problema de simulación “la población” es el modelo y lo conocemos por completo (no obstante el problema de simulación puede surgir como solución de un problema de inferencia).↩︎