7.2 Muestreo por importancia

Para aproximar la integral: \[\theta = E\left( h\left( X\right) \right) = \int h\left( x\right) f(x)dx,\] puede ser preferible generar observaciones de una densidad \(g\) que tenga una forma similar al producto \(hf\).

Si \(Y\sim g\): \[\theta = \int h\left( x\right) f(x)dx = \int \frac{h\left( x\right) f(x)}{g(x)}g(x)dx = E\left( q\left( Y\right) \right).\] siendo \(q\left( x\right) = \frac{h\left( x\right) f(x)}{g(x)}\).

Si \(y_1,y_2,\ldots ,y_n\) i.i.d. \(Y\sim g\): \[\theta \approx \frac{1}{n}\sum\limits_{i=1}^nq\left( y_i\right) = \frac{1}{n}\sum\limits_{i=1}^nw(y_i)h\left( y_i\right) = \hat{\theta}_{g}\] con \(w(y) = \frac{f(y)}{g(y)}\).

En este caso \(Var(\hat{\theta}_{g}) = Var\left( q\left( Y\right) \right) /n\), pudiendo reducirse significativamente respecto al método clásico si: \[g(x)\underset{aprox.}{\propto } \left\vert h(x) \right\vert f(x),\] ya que en ese caso \(\left\vert q(x) \right\vert\) sería aproximadamente constante (puede demostrarse fácilmente que la varianza es mínima si esa relación es exacta).

Para garantizar la convergencia de la aproximación por simulación, la varianza del estimador \(\hat{\theta}_{g}\) debería ser finita, i.e.: \[E\left( q^2\left( Y\right) \right) = \int \frac{h^2\left( x\right)f^2(x)}{g(x)}dx = E\left( h^2\left( X\right) \frac{f(X)}{g(X)}\right) < \infty.\] La idea básica es que si la densidad \(g\) tiene colas más pesadas que la densidad \(f\) con mayor facilidad puede dar lugar a “simulaciones” con varianza finita (podría emplearse en casos en los que no existe \(E \left( h^2 \left( X \right) \right)\); ver Sección 3.1).

La distribución de los pesos \(w(y_i)\) debería ser homogénea para evitar datos influyentes (que introducirían inestabilidad en la aproximación).

Ejemplo 7.3

Podríamos aproximar la integral del Ejemplo 7.2 anterior empleando muestreo por importancia considerando como densidad auxiliar una exponencial de parámetro \(\lambda=1\) truncada en \(t\): \[g(x) = \lambda e^{-\lambda (x - t)}\text{, }x>t,\] (podemos emplear dexp(y - t) para evaluar esta densidad y rexp(n) + t para generar valores).

En primer lugar comparamos \(h(x)f(x)\) con la densidad auxiliar reescalada, \(g(x)f(4.5)\), para comprobar si es una buena elección:

curve(dnorm(x), 4.5, 6, ylab = "dnorm(x) y dexp(x-4.5)*k")
abline(v = 4.5)
abline(h = 0)
escala <- dnorm(4.5)  # Reescalado para comparación...
curve(dexp(x - 4.5) * escala, add = TRUE, lty = 2)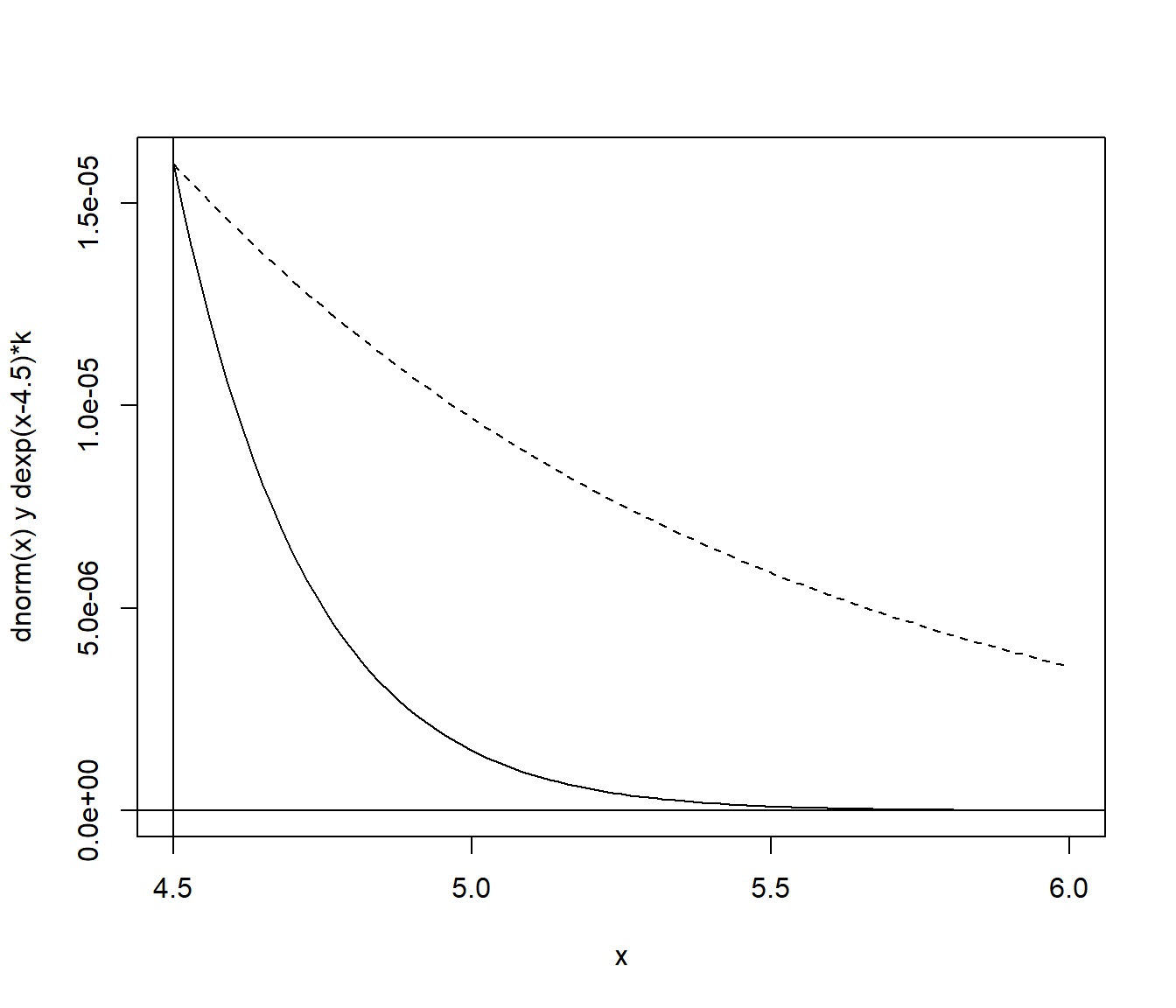
Objetivo a integrar (densidad objetivo truncada) y densidad auxiliar reescalada.

Figura 7.3: Objetivo a integrar (densidad objetivo truncada) y densidad auxiliar reescalada.

Generamos valores de la densidad auxiliar y calculamos los pesos:

set.seed(1)
nsim <- 10^3
y <- rexp(nsim) + 4.5    #  Y ~ g
w <- dnorm(y)/dexp(y - 4.5)

La aproximación por simulación sería mean(w * h(y)):

# h(x) <- function(x) x > 4.5  # (1 si x > 4.5 => h(y) = 1)
mean(w) # mean(w*h(y))
## [1] 3.144811e-06
pnorm(-4.5)  # valor teórico
## [1] 3.397673e-06

Representamos gráficamente la aproximación en función del número de simulaciones:

plot(cumsum(w)/1:nsim, type = "l", ylab = "Aproximación", xlab = "Iteraciones")
abline(h = pnorm(-4.5), lty = 2, col = "blue")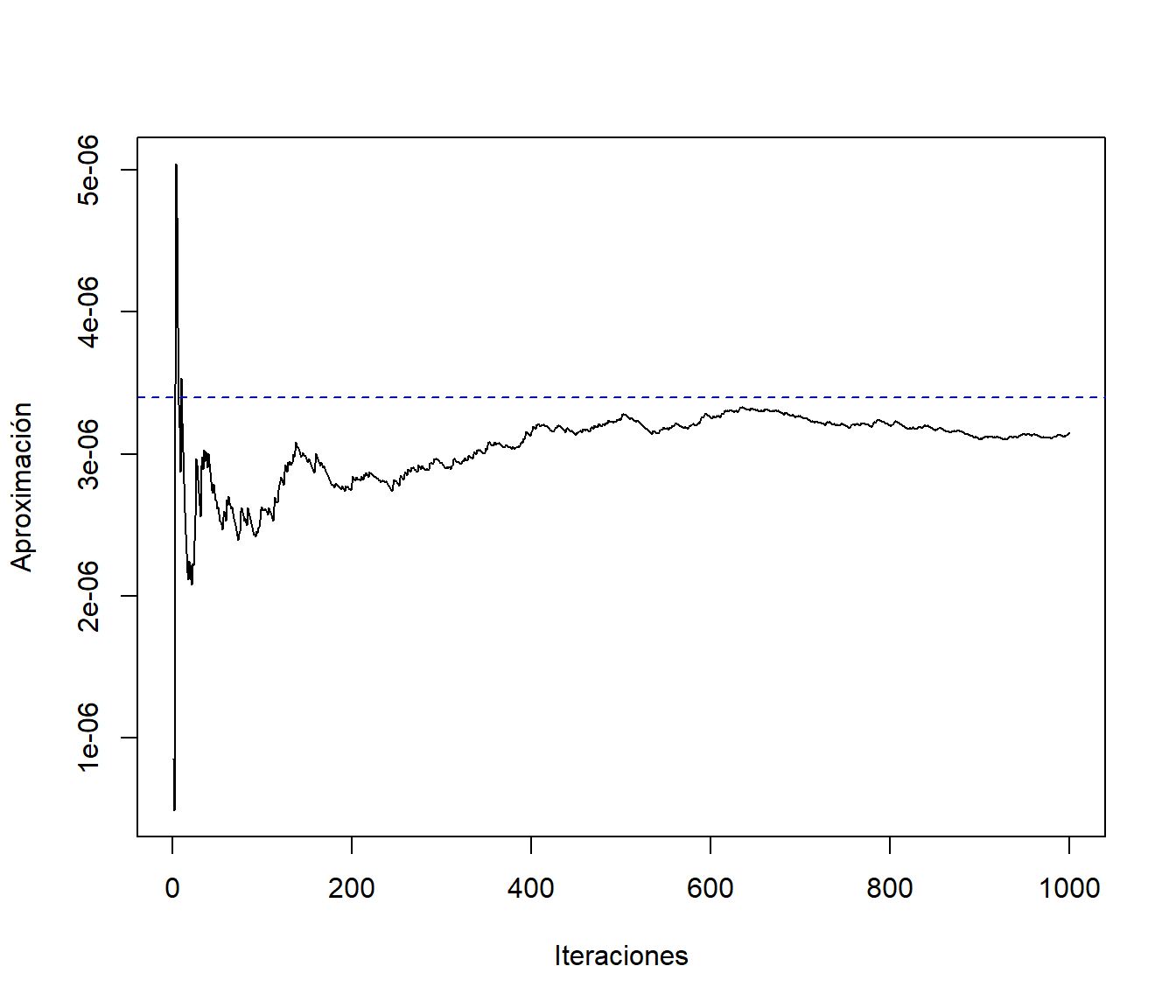
Convergencia de la aproximación de la integral mediante muestreo por importancia.

Figura 7.4: Convergencia de la aproximación de la integral mediante muestreo por importancia.

El error estándar de la aproximación sería sqrt(var(w * h(y))/nsim):

sqrt(var(w)/nsim) # sd(w*h(y))/sqrt(nsim)   
## [1] 1.371154e-07

Mientras que empleando la aproximación tradicional:

est <- mean(rnorm(nsim) > 4.5)
est
## [1] 0
sqrt(est * (1 - est)/nsim)
## [1] 0

Ejemplo 7.4 (muestreo por importancia con mala densidad auxiliar)

Supongamos que se pretende aproximar \(P\left(2<X<6\right)\) siendo \(X\sim Cauchy(0,1)\) empleando muestreo por importancia y considerando como densidad auxiliar la normal estándar \(Y\sim N(0,1)\). Representaremos gráficamente la aproximación y estudiaremos los pesos \(w(y_i)\).

Nota: En este caso van a aparecer problemas (la densidad auxiliar debería tener colas más pesadas que la densidad objetivo; sería adecuado si intercambiáramos las distribuciones objetivo y auxiliar, como en el Ejemplo 7.5 siguiente).

Se trata de aproximar pcauchy(6) - pcauchy(2), i.e. f(y) = dcauchy(y) y h(y) = (y > 2) * (y < 6), empleando muestreo por importancia con g(y) = dnorm(y).

nsim <- 10^5
set.seed(4321)
y <- rnorm(nsim)
w <- dcauchy(y)/dnorm(y) # w <- w/sum(w) si alguna es una cuasidensidad

La aproximación por simulación es mean(w(y) * h(y)):

mean(w * (y > 2) * (y < 6)) 
## [1] 0.09929348
pcauchy(6) - pcauchy(2)  # Valor teórico
## [1] 0.09501516

Si se estudia la convergencia:

plot(cumsum(w * (y > 2) * (y < 6))/1:nsim, type = "l", ylab = "Aproximación", xlab = "Iteraciones")
abline(h = pcauchy(6) - pcauchy(2), lty = 2, col = "blue")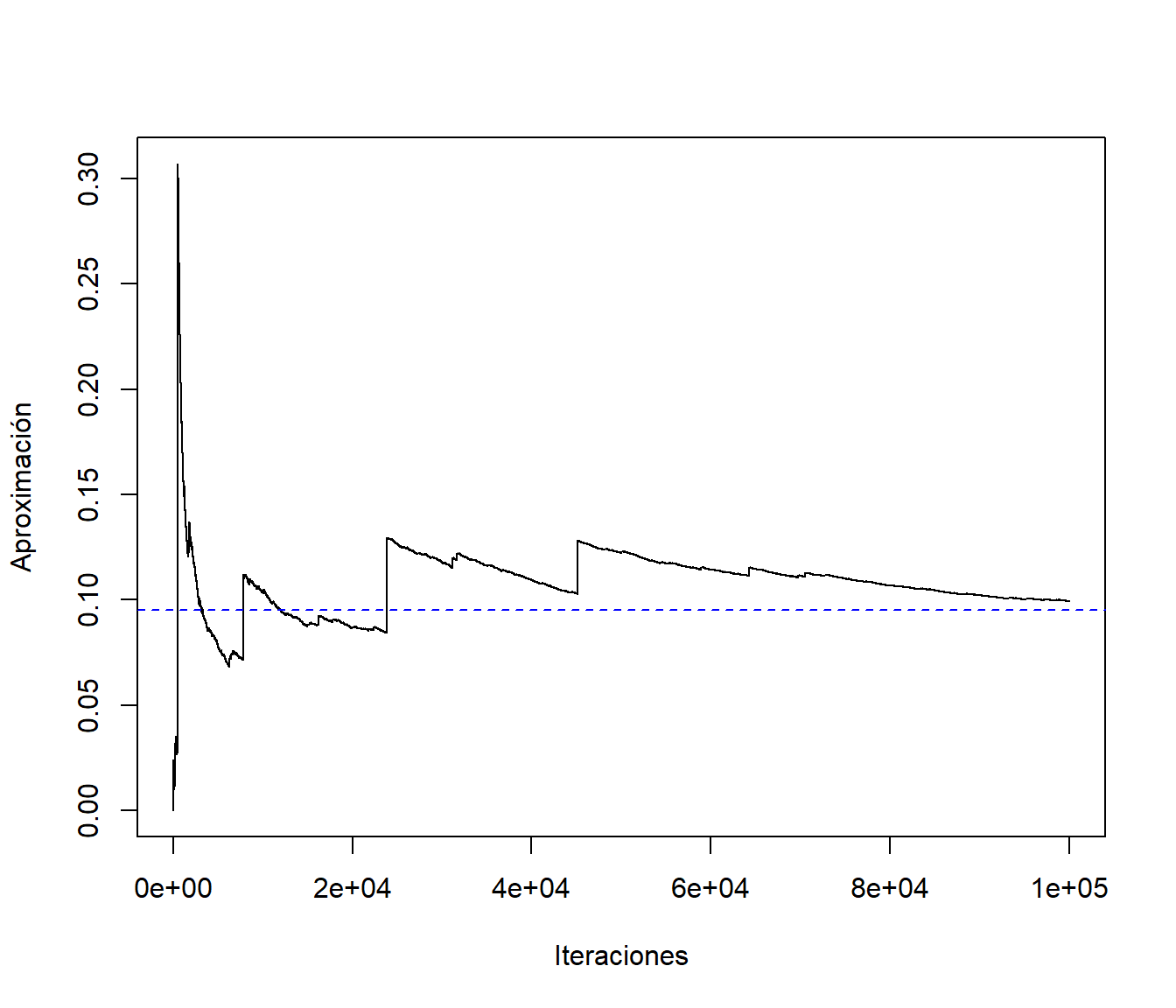
Gráfico de convergencia de la aproximación mediante muestreo por importancia con mala densidad auxiliar.

Figura 7.5: Gráfico de convergencia de la aproximación mediante muestreo por importancia con mala densidad auxiliar.

Lo que indica es una mala elección de la densidad auxiliar.

La distribución de los pesos debería ser homogénea. Por ejemplo, si los reescalamos para que su suma sea el número de valores generados, deberían tomar valores en torno a uno:

boxplot(nsim * w/sum(w))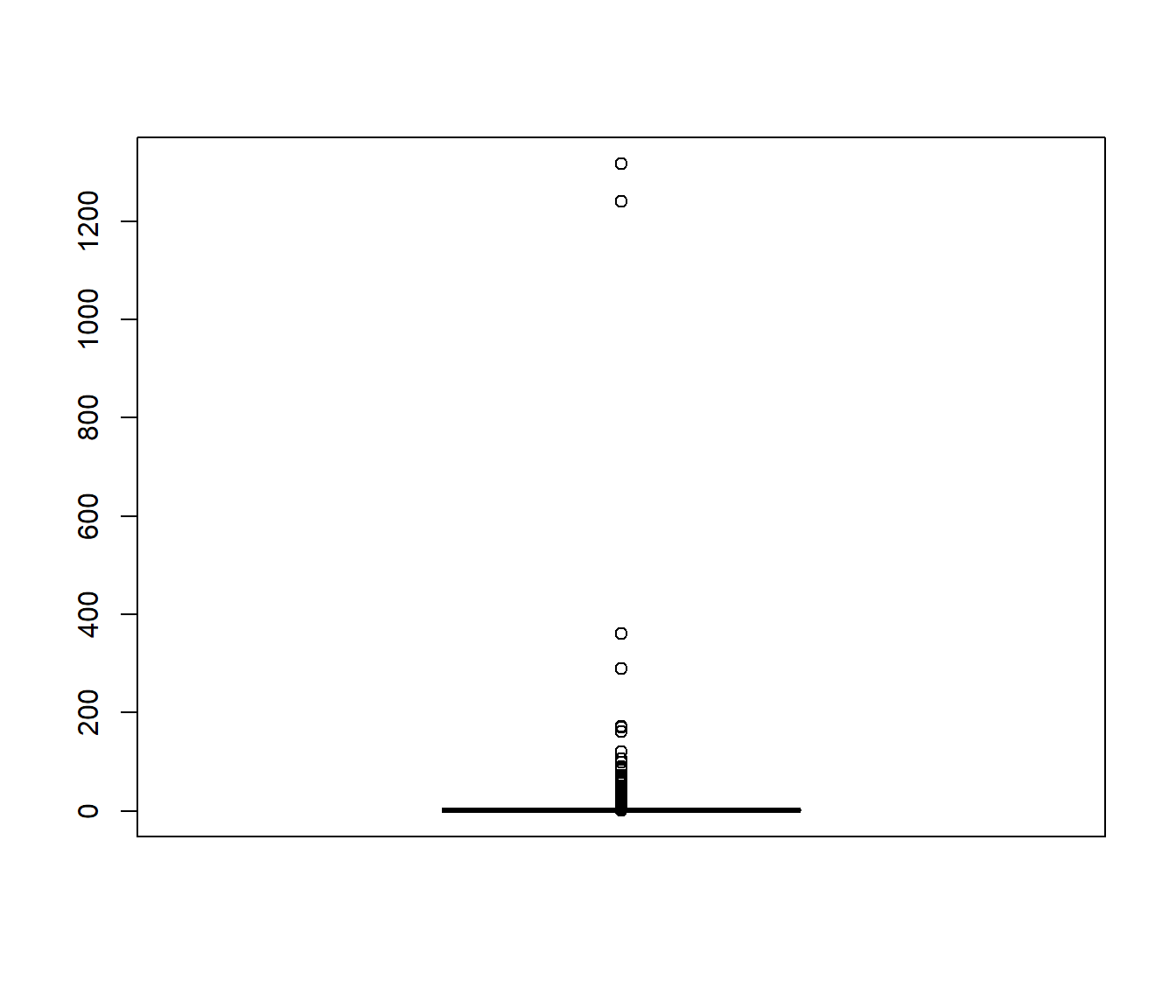
Gráfico de cajas de los pesos del muestreo por importancia reescalados (de forma que su media es 1).

Figura 7.6: Gráfico de cajas de los pesos del muestreo por importancia reescalados (de forma que su media es 1).

7.2.1 Remuestreo (del muestreo) por importancia

Cuando \(f\) y/o \(g\) son cuasi-densidades, para evitar calcular constantes normalizadoras, se emplea como aproximación: \[\theta \approx \frac{\sum\limits_{i=1}^n w(y_i) h\left( y_i\right) }{ \sum\limits_{i=1}^n w(y_i)}.\] De hecho este estimador es empleado muchas veces en lugar del anterior ya que, aunque en general no es insesgado, puede ser más eficiente si \(w(Y)\) y \(w(Y)h(Y)\) están altamente correlacionadas (e.g. Liu, 2004, p.35).

Adicionalmente, puede verse que con un muestreo de \(\left\{y_1, y_2, \ldots, y_n \right\}\) ponderado por \(w(y_i)\) (prob. \(=w(y_i)\left/ \sum\nolimits_{i=1}^n w(y_i) \right.\) ) se obtiene una simulación aproximada de \(f\) (Sample importance resampling, Rubin, 1987).

Ejemplo 7.5 (simulación de normal estándar a partir de Cauchy; Sampling Importance Resampling)

Generamos 1000 simulaciones de una distribución (aprox.) \(N(0,1)\) (densidad objetivo) mediante remuestreo del muestreo por importancia de \(10^{5}\) valores de una \(Cauchy(0,1)\) (densidad auxiliar).

Nota: En este caso f(y) = dnorm(y) y g(y) = dcauchy(y), al revés del Ejemplo 7.4 anterior.

# Densidad objetivo
# f <- dnorm # f <- function(x) ....

nsim <- 10^3
# El nº de simulaciones de la densidad auxiliar debe ser mucho mayor:
nsim2 <- 10^5
set.seed(4321)
y <- rcauchy(nsim2)
w <- dnorm(y)/dcauchy(y) # w <- w/sum(w) si alguna es una cuasidensidad

# Si se pidiera aproximar una integral
# h(y) = y si es la media # h <- function(y) y
# mean(w * h(y))

Sampling Importance Resampling:

rx <- sample(y, nsim, replace = TRUE, prob = w/sum(w))
hist(rx, freq = FALSE, breaks = "FD", ylim = c(0, 0.5))
lines(density(rx))
curve(dnorm, col = "blue", add = TRUE)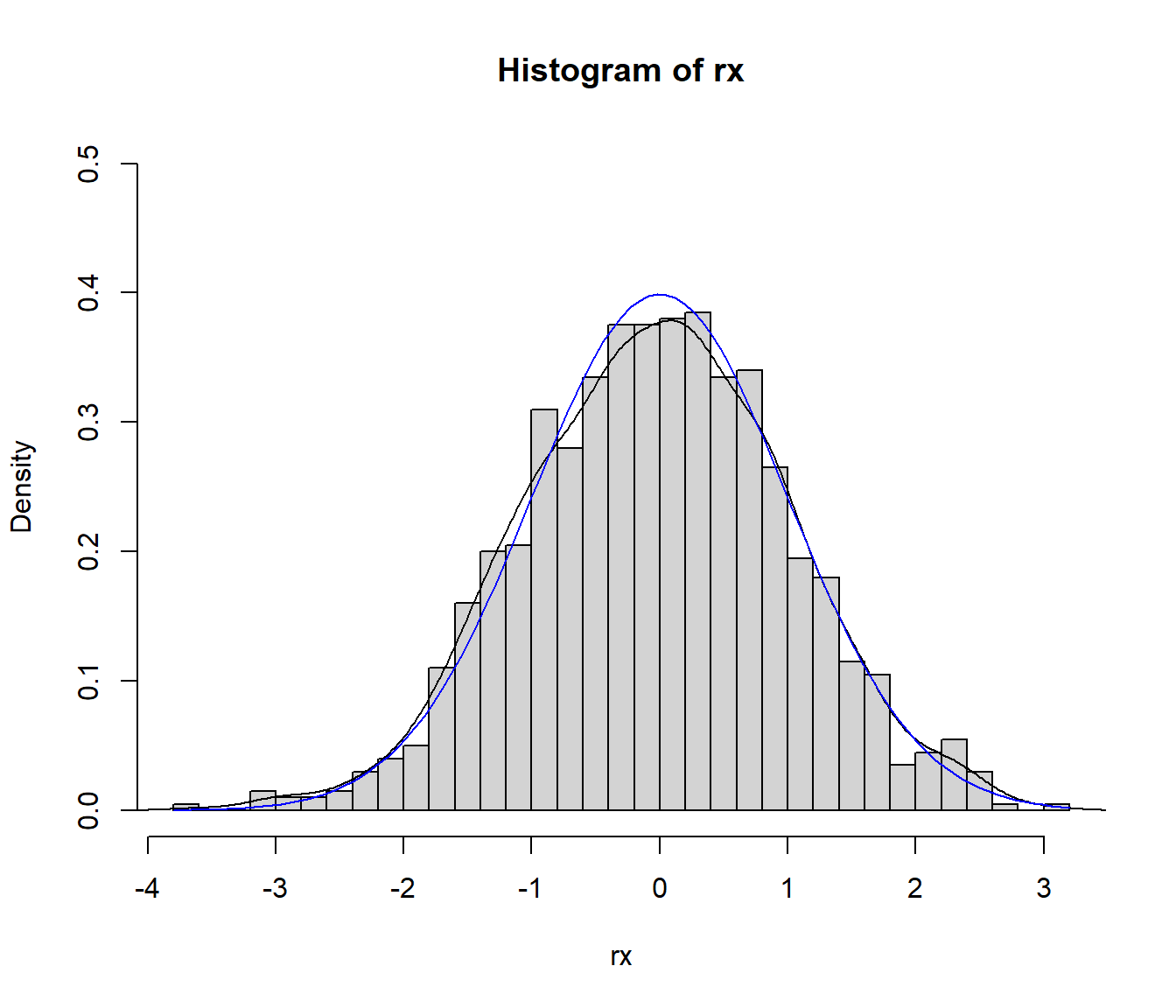
Distribución de los valores generados mediante remuestreo por importancia y densidad objetivo.

Figura 7.7: Distribución de los valores generados mediante remuestreo por importancia y densidad objetivo.

Nota: Si f o g fuesen cuasidensidades y se pidiese aproximar la integral, habría que reescalar los pesos w <- f(y)/g(y) en la aproximación por simulación, resultando sum(w * h(y))/sum(w) (media ponderada) y en el análisis de convergencia se emplearía cumsum(w * h(y))/cumsum(w).

Ejercicio 7.1 (propuesto)

Consideramos una variable aleatoria con densidad: \[f(x)\propto e^{-x}\cos^{2}(x),\text{ si }x>0.\]

  1. Aproximar mediante integración Monte Carlo la media de esta distribución (\(h(x)=x\)) empleando muestreo de importancia con distribución auxiliar una exponencial de parámetro \(\lambda=1\) a partir de 10000 simulaciones (OJO: se conoce la cuasi-densidad de la variable aleatoria de interés, emplear la aproximación descrita en apuntes).

  2. Generar 500 simulaciones (aprox.) de la distribución de interés mediante remuestreo del muestreo por importancia.

NOTA: En el último apartado, para comprobar que los valores generados proceden de la distribución objetivo, si representamos la cuasidensidad \(f^{\ast}(x) = e^{-x}\cos^{2}(x)\) junto con el histograma (en escala de densidades, freq = FALSE), hay que tener en cuenta que faltaría dividir la cuasidensidad por una constante normalizadora para poder compararlos directamente. Si no se reescala la cuasidensidad, podríamos compobar si la forma es similar (si la distribución de los valores generados es proporcional a la cuasidensidad, con mayor concentración donde la cuasidensidad se aleja de 0). En este caso (como \(g\) es una densidad) podríamos estimar la constante normalizadora (\(f(x) = \frac{1}{c}f^{\ast}(x)\)) a partir de los pesos del muestreo por importancia (c.approx <- mean(w); en este caso concreto \(c=\frac{3}{5}\)).