10.2 Bootstrap paramétrico

Supongamos que sabemos que la función de distribución poblacional pertenece a cierta familia paramétrica. Es decir \(F=F_{\theta }\) para algún vector \(d\)-dimensional \(\theta \in \Theta\). En ese caso parece lógico estimar \(\theta\) a partir de la muestra (denotemos \(\hat{\theta}\) un estimador de \(\theta\), por ejemplo el de máxima verosimilitud) y obtener remuestras de \(F_{\hat{\theta}}\) no de \(F_n\). Entonces, el bootstrap uniforme se modifica de la siguiente forma, dando lugar al llamado bootstrap paramétrico:

  1. Dada la muestra \(\mathbf{X}=\left( X_1,\ldots ,X_n \right)\), calcular \(\hat{\theta}\)

  2. Para cada \(i=1,\ldots ,n\) generar \(X_i^{\ast}\) a partir de \(F_{\hat{\theta}}\)

  3. Obtener \(\mathbf{X}^{\ast}=\left( X_1^{\ast},\ldots ,X_n^{\ast} \right)\)

  4. Calcular \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_{\hat{\theta}} \right)\)

  5. Repetir \(B\) veces los pasos 2-4 para obtener las réplicas bootstrap \(R^{\ast (1)}\), \(\ldots\), \(R^{\ast (B)}\)

  6. Utilizar esas réplicas bootstrap para aproximar la distribución en el muestreo de \(R\)

En el paso 2, debemos poder simular valores de la distribución \(F_{\hat{\theta}}\). Como ya hemos visto en la Sección 1.3, en R (y en la mayoría de lenguajes de programación y software estadístico) se dispone de rutinas que permiten simular la mayoría de las distribuciones paramétricas habituales. En otros casos habrá que emplear métodos generales, preferiblemente el método de inversión descrito en el Capítulo 4.

Una de las principales aplicaciones del bootstrap paramétrico es el contraste de hipótesis que se tratará en la Sección 11.3.1.

Ejemplo 10.2 (Inferencia sobre la media, continuación)

Continuando con el Ejemplo 9.2 del tiempo de vida de microorganismos, podríamos pensar en emplear bootstrap paramétrico para calcular un intervalo de confianza para la media poblacional.

La valided de los resultados dependerá en gran medida de que el modelo paramétrico sea adecuado para describir la variabilidad de los datos. En este caso parece razonable asumir una distribución exponencial (no lo es que el modelo admita tiempos de vida negativos, como ocurriría al asumir normalidad):

muestra <- simres::lifetimes
# Distribución bootstrap uniforme
# plot(ecdf(muestra), xlim = c(-.5, 3), ylab = "F(x)")
curve(ecdf(muestra)(x), xlim = c(-.5, 3), ylab = "F(x)", type = "s")
# Distribución bootstrap paramétrico normal
curve(pnorm(x, mean(muestra), sd(muestra)), lty = 2, add = TRUE)
# Distribución bootstrap paramétrico exponencial
curve(pexp(x, 1/mean(muestra)), lty = 3, add = TRUE)
legend("bottomright", legend = c("Empírica", "Aprox. normal", "Aprox. exponencial"), 
       lty = 1:3)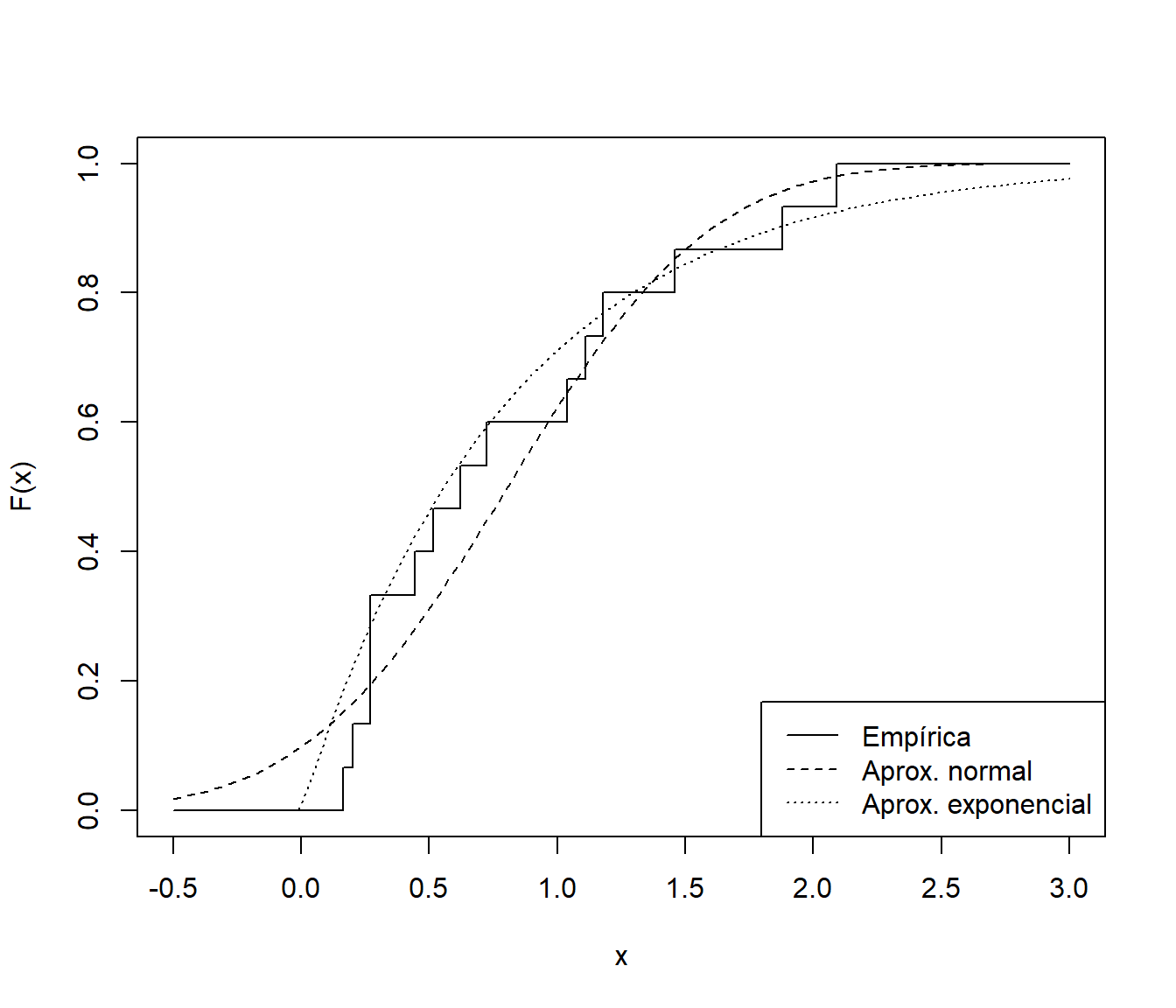
Distribución empírica de la muestra de tiempos de vida de microorganismos y aproximaciones paramétricas.

Figura 10.2: Distribución empírica de la muestra de tiempos de vida de microorganismos y aproximaciones paramétricas.

Podemos modificar fácilmente el código mostrado en el Ejemplo 9.2, de forma que se emplee bootstrap paramétrico (exponencial):

n <- length(muestra)
alfa <- 0.05
# Estimaciones muestrales
x_barra <- mean(muestra)
cuasi_dt <- sd(muestra)
# Remuestreo
set.seed(1)
B <- 1000
estadistico_boot <- numeric(B)
for (k in 1:B) {
  # remuestra <- sample(muestra, n, replace = TRUE)
  remuestra <- rexp(n, 1/x_barra)
  x_barra_boot <- mean(remuestra)
  cuasi_dt_boot <- sd(remuestra)
  estadistico_boot[k] <- sqrt(n) * (x_barra_boot - x_barra)/cuasi_dt_boot
}
# Aproximación Monte Carlo de los ptos críticos:
pto_crit <- quantile(estadistico_boot, c(alfa/2, 1 - alfa/2))
# Construcción del IC
ic_inf_boot <- x_barra - pto_crit[2] * cuasi_dt/sqrt(n)
ic_sup_boot <- x_barra - pto_crit[1] * cuasi_dt/sqrt(n)
IC_boot <- c(ic_inf_boot, ic_sup_boot)
names(IC_boot) <- paste0(100*c(alfa/2, 1-alfa/2), "%")
IC_boot
##      2.5%     97.5% 
## 0.5319787 1.3961382

Para emplear el paquete boot, como se comentó en la Sección 9.3.1, habría que establecer en la llamada a la función boot() los argumentos: sim = "parametric", mle igual a los parámetros necesarios para la simulación y ran.gen = function(data, mle), una función de los datos originales y de los parámetros que devuelve los datos generados. En este caso además, la función statistic no necesita el vector de índices como segundo parámetro. Por ejemplo, para calcular el intervalo de confianza para la media del tiempo de vida de los microorganismos, podríamos utilizar el siguiente código:

library(boot)
ran.gen.exp <- function(data, mle) {
    # Función para generar muestras aleatorias exponenciales
    # mle contendrá la media de los datos originales
    out <- rexp(length(data), 1/mle)
    out
}

statistic <- function(data){
    c(mean(data), var(data)/length(data))
}

set.seed(1)
res.boot <- boot(muestra, statistic, R = B, sim = "parametric",
                 ran.gen = ran.gen.exp, mle = mean(muestra))

boot.ci(res.boot, type = "stud")
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = res.boot, type = "stud")
## 
## Intervals : 
## Level    Studentized     
## 95%   ( 0.5308,  1.4061 )  
## Calculations and Intervals on Original Scale

Ejemplo 10.3 (Inferencia sobre el máximo de una distribución uniforme, continuación) En el Ejemplo 10.1 la distribución poblacional era uniforme. Si se dispusiese de esa información, lo natural sería utilizar un bootstrap paramétrico, consistente en obtener las remuestras bootstrap a partir de una distribución uniforme con parámetro estimado: \[\mathbf{X}^{\ast}=\left( X_1^{\ast}\text{, }X_2^{\ast}\text{, }\ldots \text{, }X_n^{\ast} \right), \text{ con } X_i^{\ast} \sim \mathcal{U}\left( 0,\hat{\theta}\right).\] En estas circunstancias es muy sencillo obtener la distribución en el remuestreo de \(\hat{\theta}^{\ast}\), ya que su deducción es totalmente paralela a la de la distribución en el muestreo de \(\hat{\theta}\). Así, la función de densidad de \(\hat{\theta}^{\ast}\) es \[\hat{g}\left( x \right) =\frac{n}{\hat{\theta}}\left( \frac{x}{\hat{\theta}} \right)^{n-1},\text{ si }x\in \left[ 0,\hat{\theta}\right] .\]

Con lo cual, al utilizar un bootstrap paramétrico, la distribución en el remuestreo de \(R^{\ast}=R\left( \mathbf{X}^{\ast},F_{\hat{ \theta}} \right) =\hat{\theta}^{\ast}-\hat{\theta}\) imita a la distribución en muestreo de \(R=R\left( \mathbf{X},F \right) =\hat{\theta}-\theta\).

Para implementarlo en la práctica podríamos emplear un código muy similar al del ejemplo original :

# Remuestreo
B <- 2000
maximo <- numeric(B)
estadistico <- numeric(B)
for (k in 1:B) {
    remuestra <- runif(n) * theta_est
    maximo[k] <- max(remuestra)
    estadistico[k] <- maximo[k] - theta_est
}
# Distribución estadístico
xlim <- c(-theta/2, 0) # c(-theta, 0)
hist(estadistico, freq = FALSE, main = "", breaks = "FD", 
     border = "darkgray", xlim = xlim)
lines(density(estadistico))
rug(estadistico, col = "darkgray")
curve(n/theta * ((x + theta)/theta)^(n - 1), col = "blue", lty = 2, lwd = 2, 
      add = TRUE)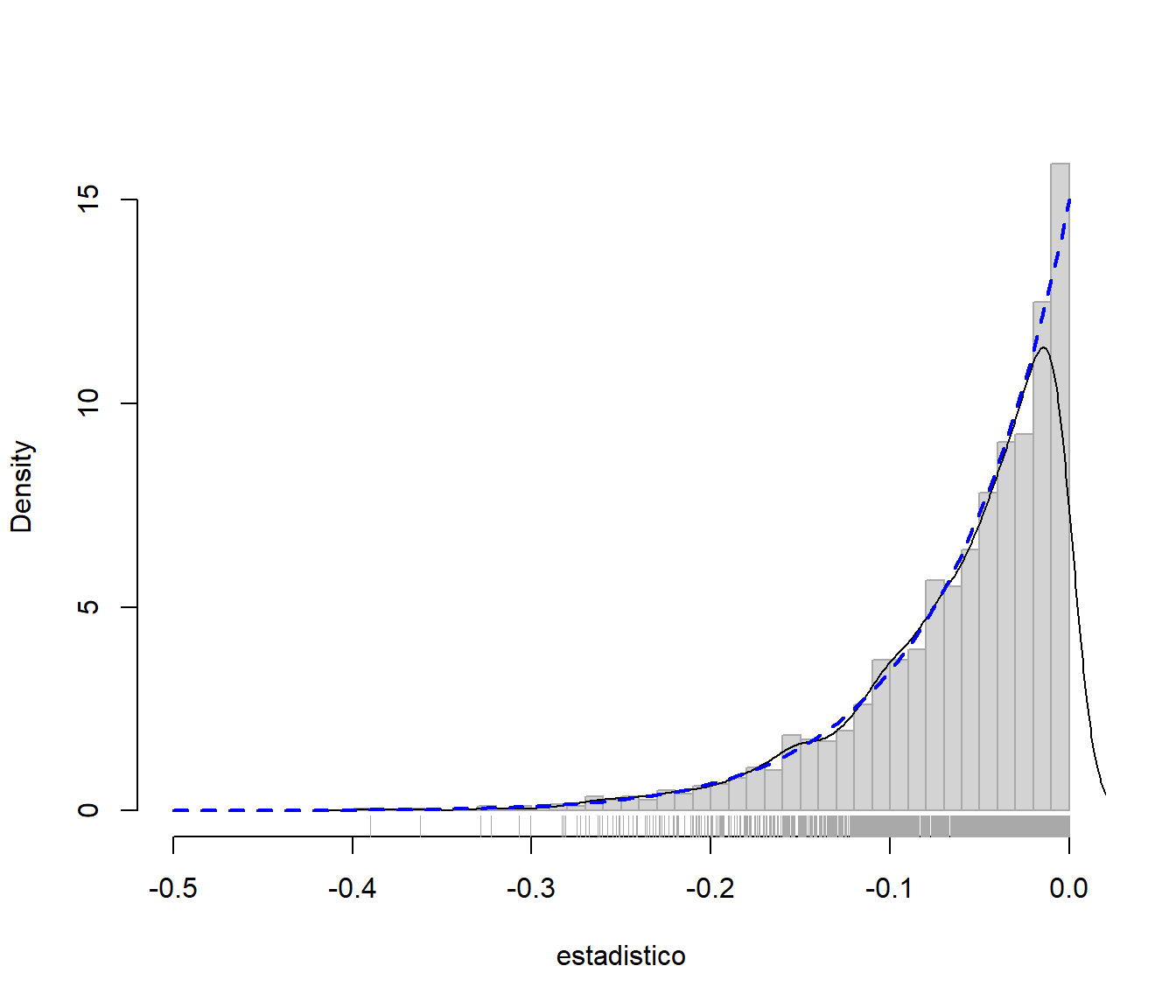
Distribución bootstrap paramétrica y distribución poblacional.

Figura 10.3: Distribución bootstrap paramétrica y distribución poblacional.