5.2 Método de la tabla guía

También conocido como método de búsqueda indexada (Indexed Search), la idea consiste en construir \(m\) subintervalos equiespaciados en \([0,1]\) de la forma: \[I_{j}=\left[ u_{j},u_{j+1}\right) =\left[ \frac{j-1}{m},\frac{j}{m}\right) \text{ para }j=1,2,\ldots ,m\] y utilizarlos como punto de partida para la búsqueda. En una tabla guía se almacenan los indices de los cuantiles correspondientes a los extremos inferiores de los intervalos: \[g_{j}=Q_{\mathcal{I}}(u_{j})=\inf \left\{ i:F_{i}\geq u_{j}=\frac{j-1}{m}\right\}\]

El punto de partida para un valor \(U\) será \(g_{j_{0}}\) con: \[j_{0}=\left\lfloor mU\right\rfloor +1\]

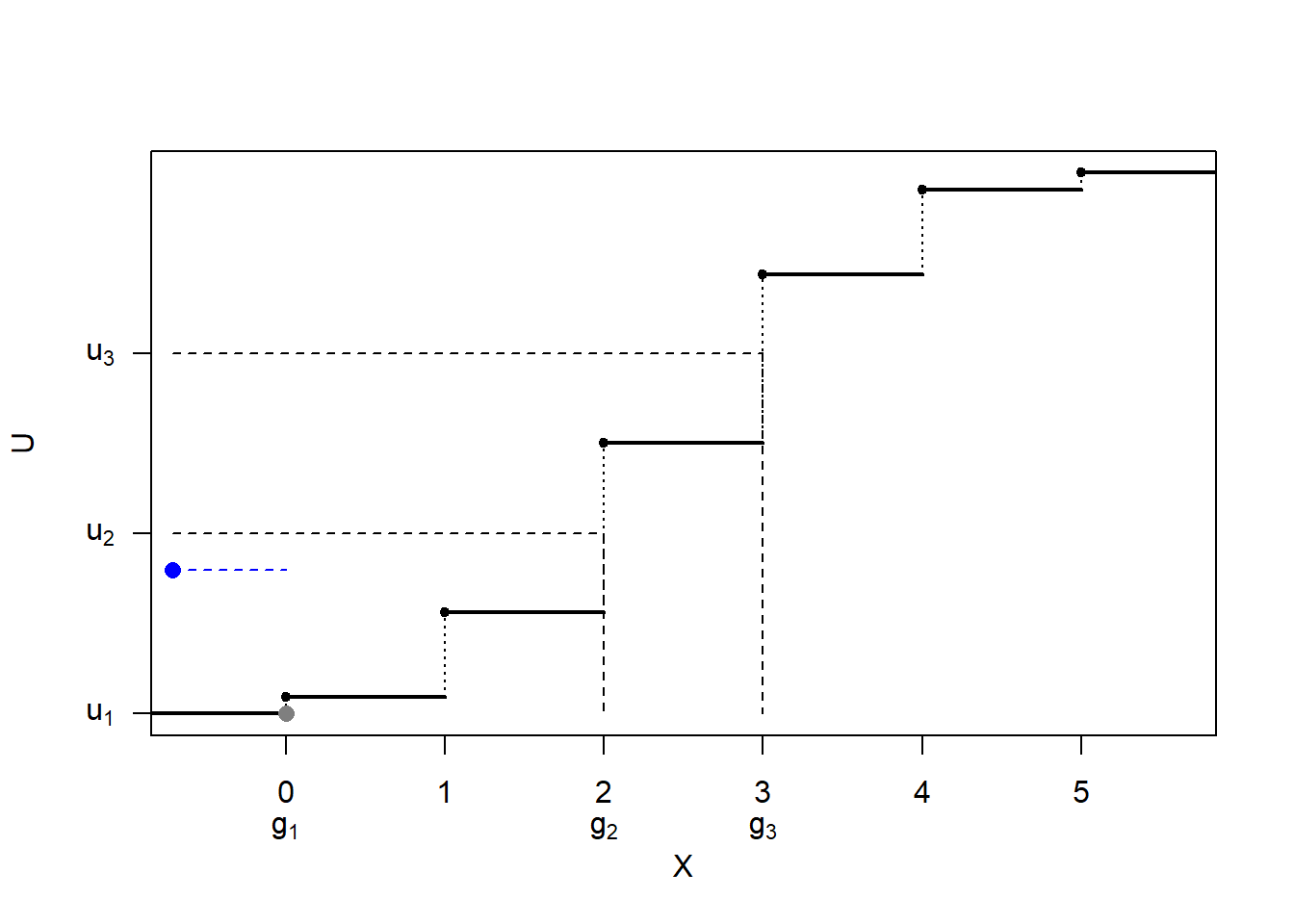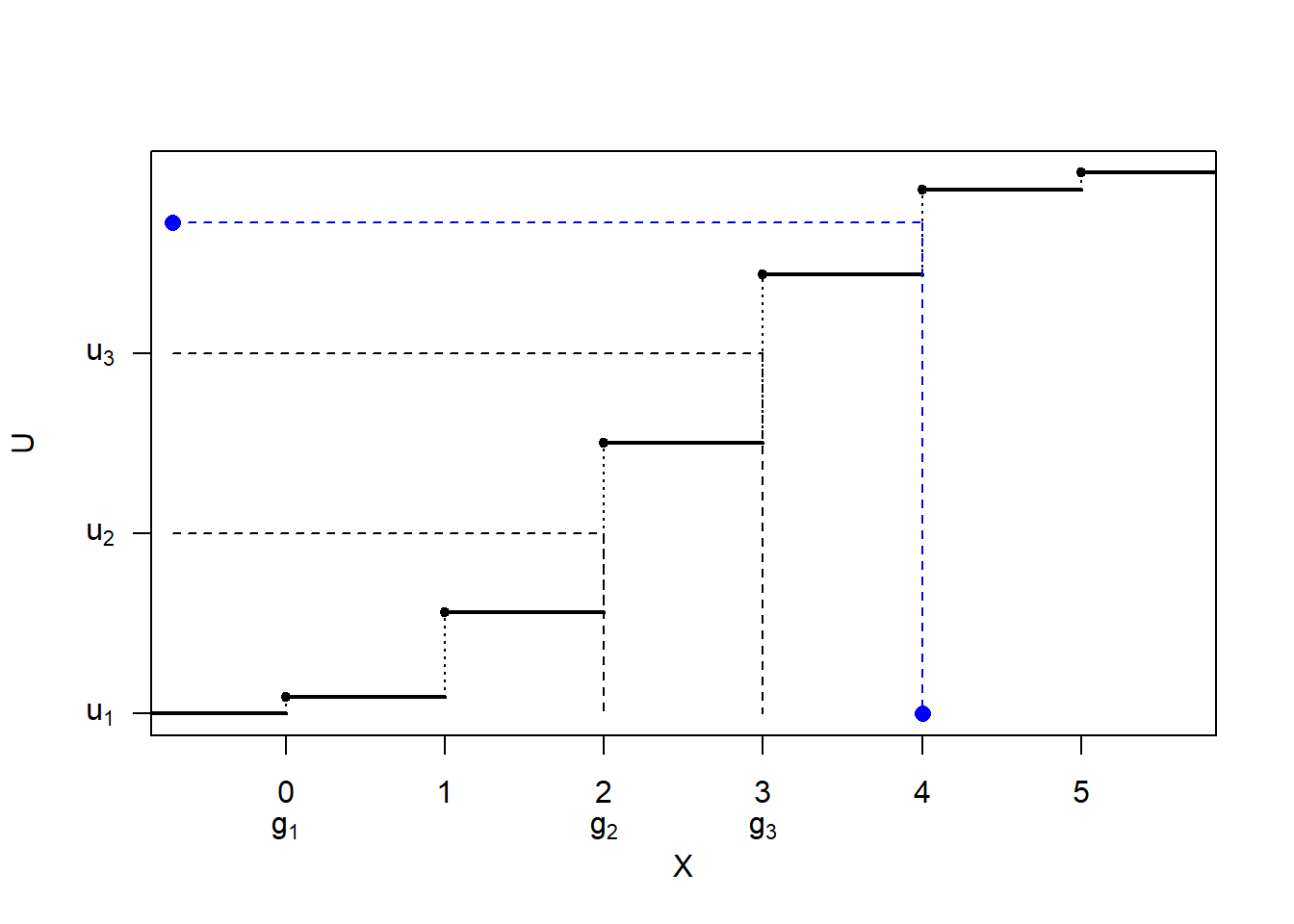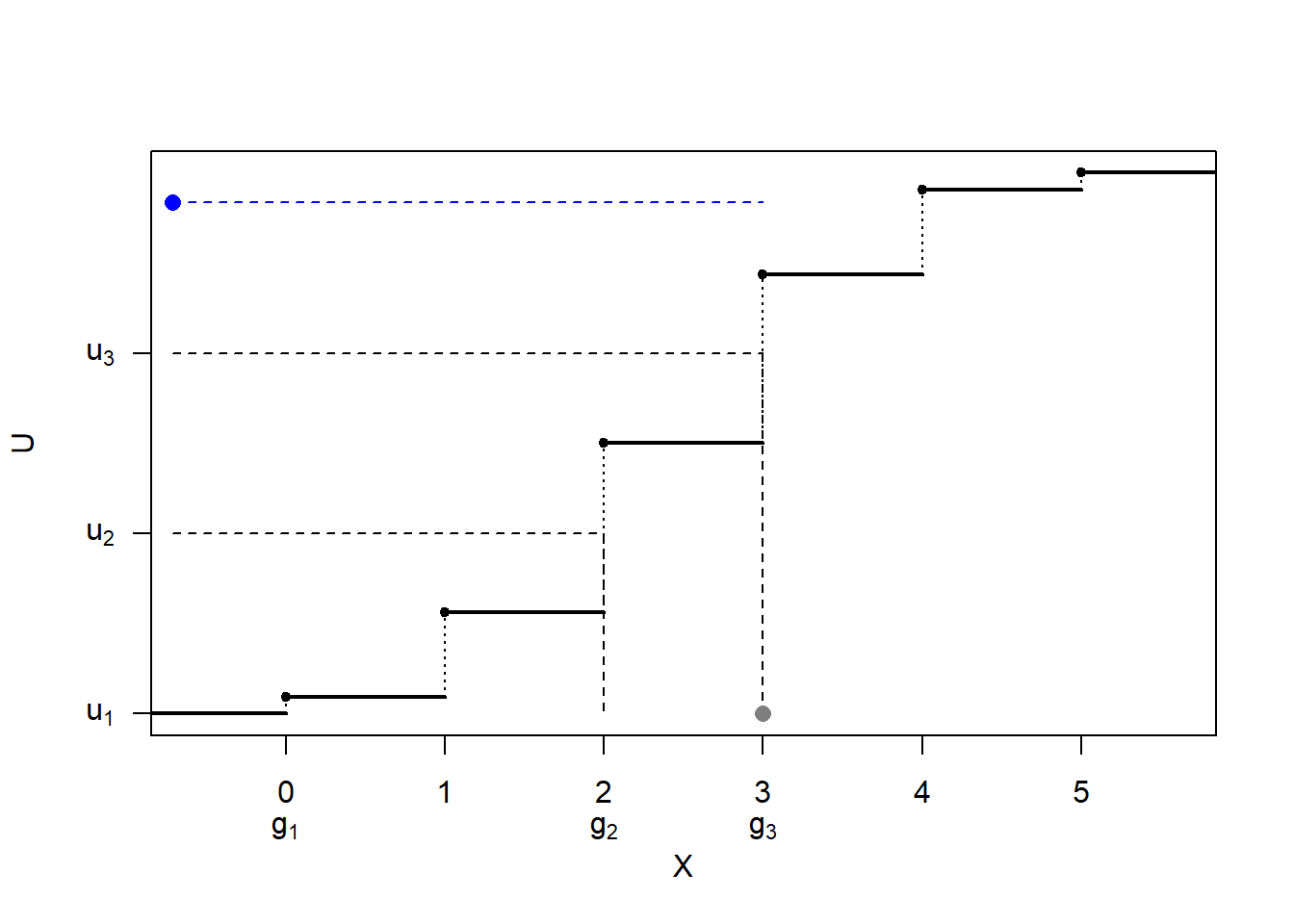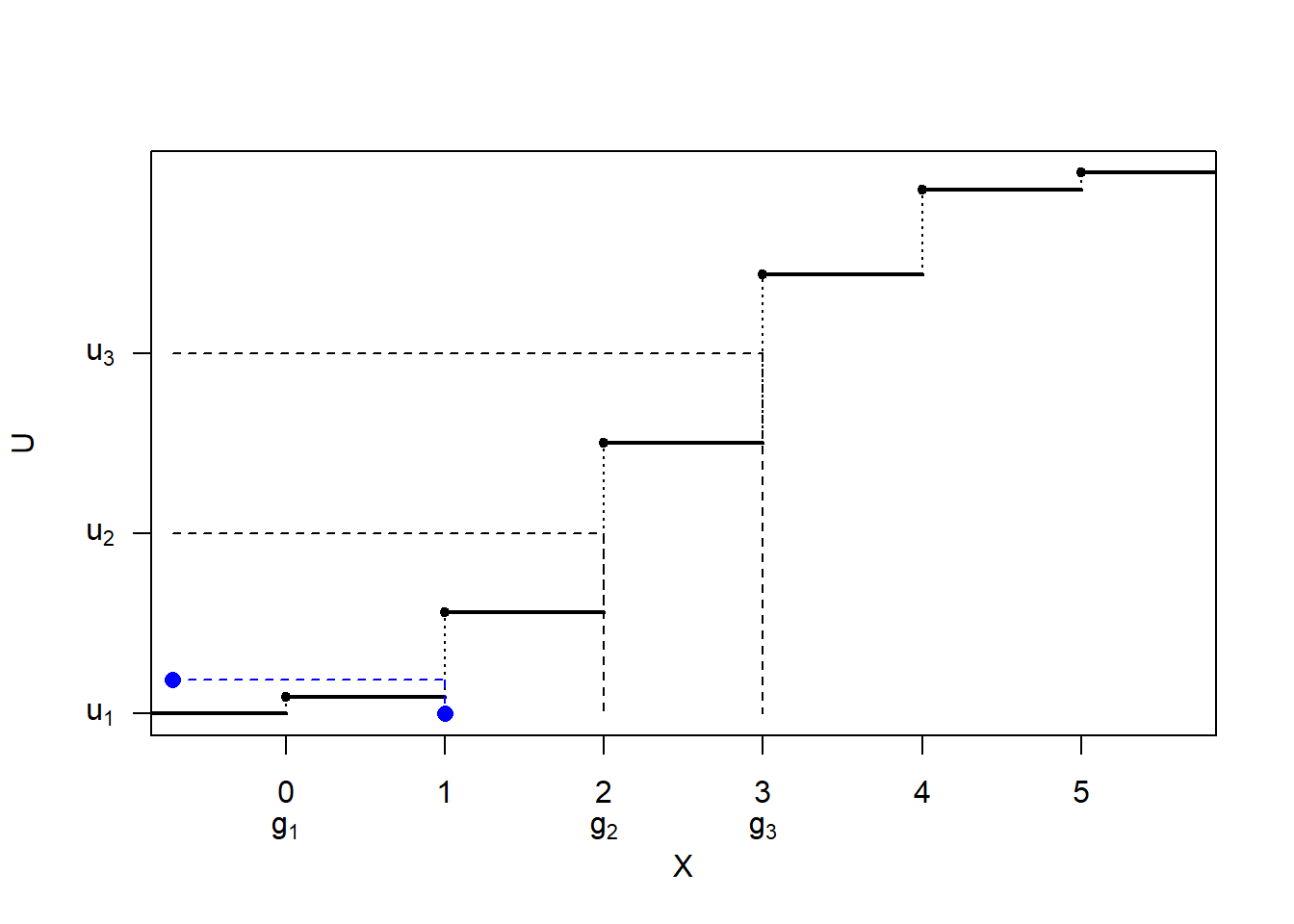
Figura 5.3: Ilustración de la simulación de una distribución discreta mediante tabla guía.

En este caso, puede verse que una cota del número medio de comparaciones es: \[E\left( N\right) \leq 1+\frac{n}{m}\]

Algoritmo 5.4 (de simulación mediante tabla guía; Chen y Asau, 1974)

Inicialización:

1. Hacer \(F_{1}=p_{1}\).

2. Desde \(i=2\) hasta \(n\) hacer \(F_{i}=F_{i-1}+p_{i}\).

Cálculo de la tabla guía:

1. Hacer \(g_{1}=1\) e \(i=1\).

2. Desde \(j=2\) hasta \(m\) hacer

   2.a Mientras \((j-1)/m>F_{i}\) hacer \(i=i+1\).

   2.b \(g_{j}=i\)

Simulación mediante tabla guía:

1. Generar \(U\sim \mathcal{U}\left( 0,1\right)\).

2. Hacer \(j=\left\lfloor mU\right\rfloor +1\).

3. Hacer \(i=g_{j}\).

4. Mientras \(U>F_{i}\) hacer \(i=i+1\).

5. Devolver \(X=x_{i}\).

Este algoritmo está implementado en la función simres::rpmf.table() (fichero rpmf.R) y devuelve también el número de comparaciones en un atributo ncomp:

rpmf.table

## function(x, prob = 1/length(x), m, n = 1000, as.factor = FALSE) {
##   # Inicializar tabla y FD
##   Fx <- cumsum(prob)
##   g <- rep(1,m)
##   i <- 1
##   for(j in 2:m) {
##     while (Fx[i] < (j-1)/m) i <- i + 1
##     g[j] <- i
##   }
##   ncomp <- i - 1
##   # Generar valores
##   X <- numeric(n)
##   U <- runif(n)
##   for(j in 1:n) {
##     i <- i0 <- g[floor(U[j] * m) + 1]
##     while (Fx[i] < U[j]) i <- i + 1
##     ncomp <- ncomp + i - i0
##     X[j] <- x[i]
##   }
##   if(as.factor) X <- factor(X, levels = x)
##   attr(X, "ncomp") <- ncomp
##   return(X)
## }
## <bytecode: 0x000001c2be34fe00>
## <environment: namespace:simres>

Ejemplo 5.3 (Simulación de una binomial mediante tabla guía)

Repetimos la simulación del Ejemplo 5.1 anterior empleando esta rutina con \(m=n-1\).

set.seed(1)
system.time( rx <- rpmf.table(x, pmf, n-1, nsim) )

##    user  system elapsed 
##    0.02    0.00    0.02

Número medio de comparaciones:

ncomp <- attr(rx, "ncomp")
ncomp/nsim

## [1] 0.55951

sum((1:length(x))*pmf) # Numero esperado con búsqueda secuencial

## [1] 6

Análisis de los resultados:

res <- table(rx)/nsim
plot(res, ylab = "frecuencia relativa", xlab = "valores")
points(x, pmf, pch = 4, col = "blue")  # Comparación teórica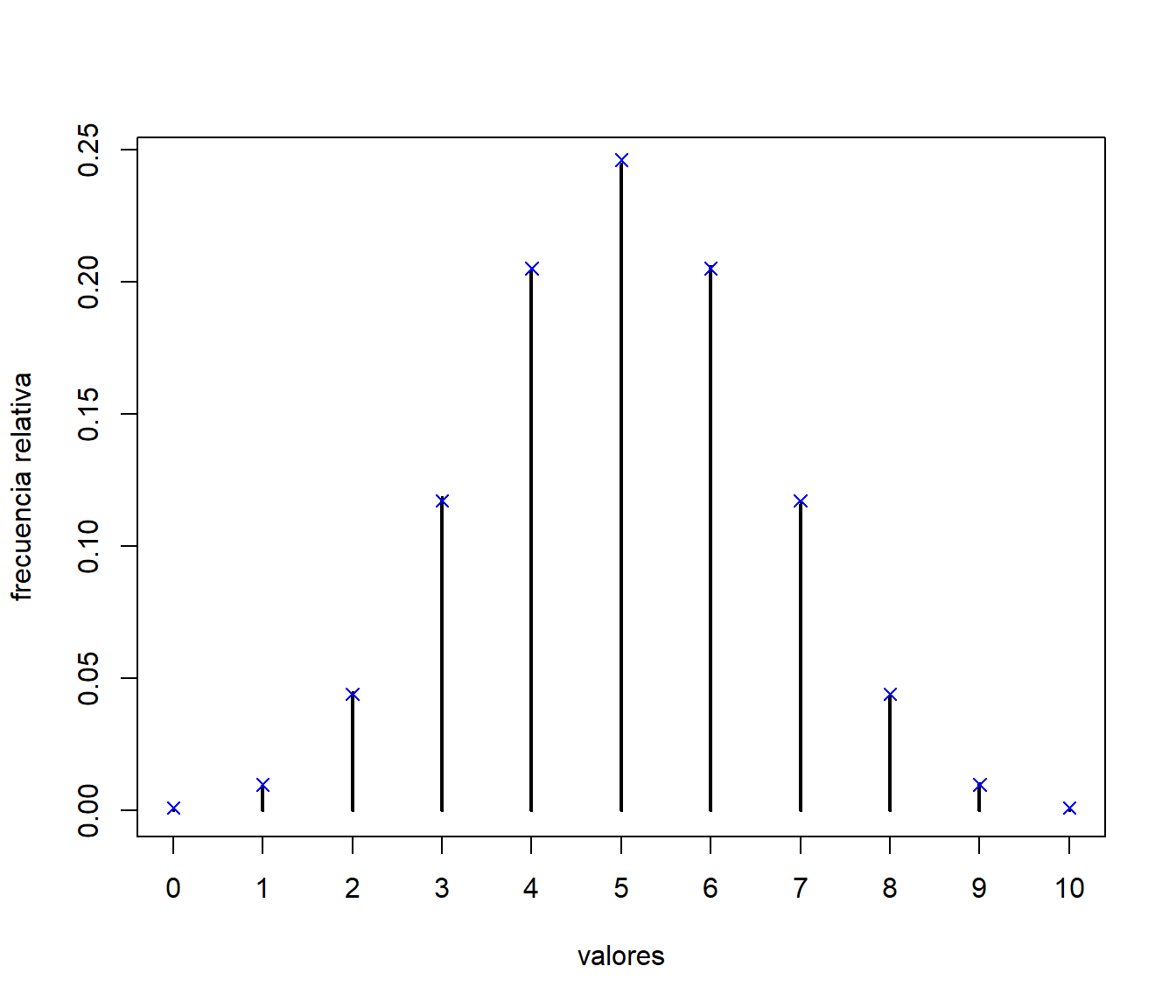

Figura 5.4: Comparación de las frecuencias relativas de los valores generados, mediante el método de la tabla guía, con las probabilidades teóricas.