5.7 Ejercicios

Ejercicio 5.1 (Simulación de una distribución mixta mediante el método de inversión generalizado)

Consideramos la variable aleatoria con función de distribución dada por: \[F(x)=\left\{ \begin{array} [c]{cl}0 & \mbox{si $x<0$}\\ \frac{x}{2}+\frac{1}{10} & \mbox{si $x\in[0,\frac{1}{5})$}\\ x+\frac{1}{10} & \mbox{si $x\in[\frac{1}{5},\frac{9}{10}]$}\\ 1 & \mbox{en otro caso} \end{array} \right.\]

Nota: Esta variable toma los valores 0 y 1/5 con probabilidad 1/10.

Esta función está implementada en el siguiente código:

fdistr <- function(x) {
ifelse(x < 0, 0,
    ifelse(x < 1/5, x/2 + 1/10,
        ifelse(x <= 9/10, x + 1/10, 1) ) )
}

Como es una función vectorial podemos emplear curve() para representarla:

curve(fdistr, from = -0.1, to = 1.1, type = 's', main = '')
abline(h = c(1/10, 2/10, 3/10), lty = 2) # Discontinuidades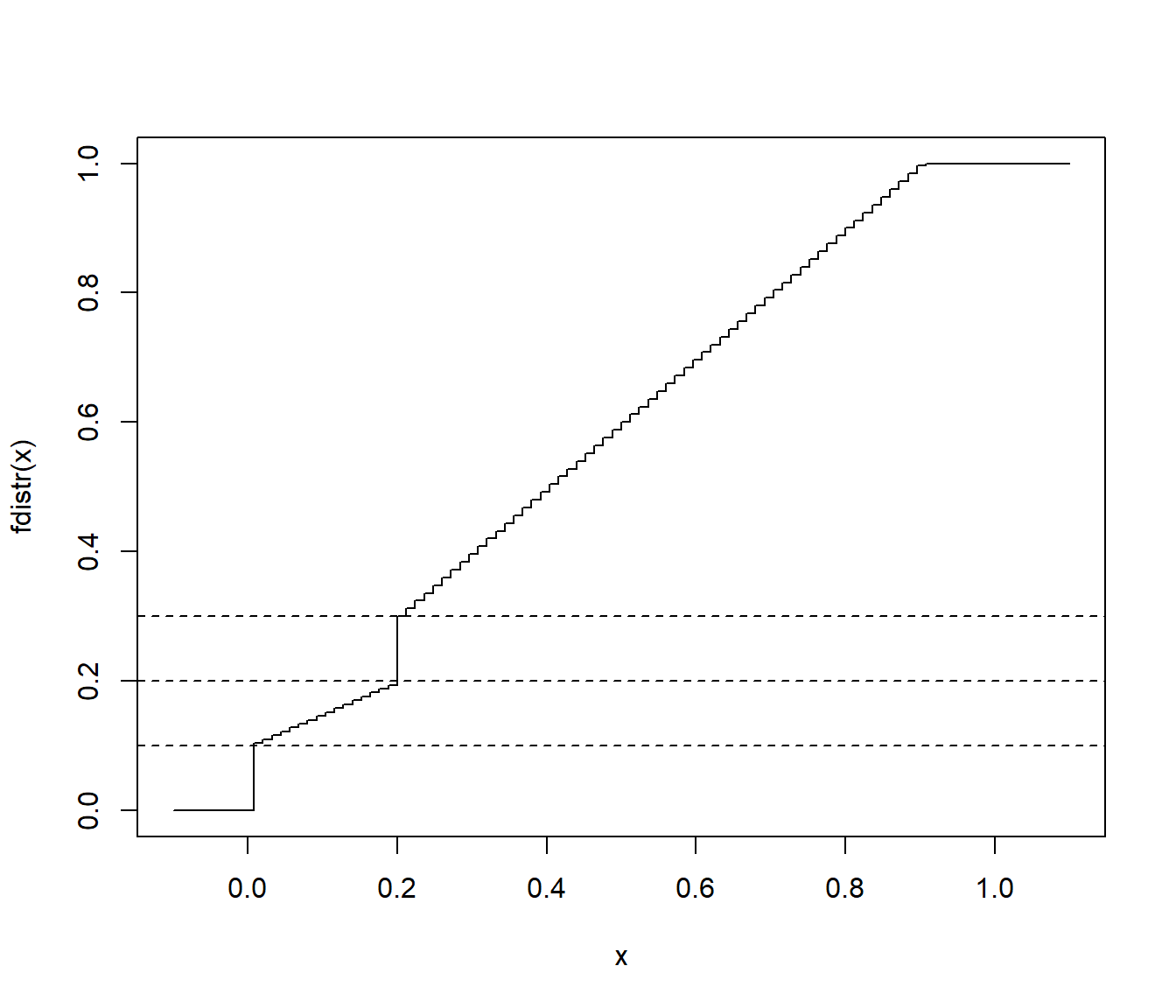
Función de distribución mixta (con discontinuidades en 0 y 1/5).

Figura 5.7: Función de distribución mixta (con discontinuidades en 0 y 1/5).

  1. Diseñar un algoritmo basado en el método de inversión generalizado para generar observaciones de esta variable.

  2. Implementar el algoritmo en una función que permita generar \(nsim\) valores de esta variable.

Ver solución en Sección D.3.1.

Ejercicio 5.2 (distribución hipergeométrica)

Se pretende simular \(nsim=10^{4}\) observaciones de una variable hipergeométrica (dhyper(x, m, n, k)) de parámetros \(m\) los dos últimos dígitos del DNI, \(n=100-m\) y \(k=20\).

  1. Comprobar que el rango de posibles valores de esta variable es max(0, k-n):min(m, k). Generar los valores empleando el método de la transformación cuantil usando búsqueda secuencial. Obtener el tiempo de CPU empleado. Aproximar por simulación la función de masa de probabilidad, representarla gráficamente y compararla con la teórica. Calcular también la media muestral (compararla con la teórica \(km/(m+n)\)) y el número medio de comparaciones para generar cada observación.

  2. Repetir el apartado anterior: ordenando previamente las probabilidades en orden decreciente, empleando la función sample de R, mediante una tabla guía (con \(k-1\) subintervalos) y usando el método de Alias.