8.3 Variables de control
En este caso se trata de sacar partido tanto a una covarianza positiva como negativa. La idea básica es emplear una variable \(Y\), con media conocida \(\mu_{Y}\), para controlar la variable \(X\) (con media desconocida), de forma que ambas variables estén “suficientemente” correlacionadas. La versión “controlada” de \(X\) será: \[X^{\ast}=X+\alpha \left( Y-\mu_{Y}\right)\] con \(E(X^{\ast})=E(X)=\theta\). Puede verse que \(Var(X^{\ast})=Var(X)+\alpha^{2}Var(Y)+2\alpha Cov(X,Y)\) es mínima para: \[\alpha^{\ast}=-\frac{Cov(X,Y)}{Var(Y)},\] con \(Var(X^{\ast}) = Var(X) \left( 1-\rho^{2} \left( X, Y \right) \right)\) (lo que supone una reducción del \(100\rho^{2}\left( X, Y \right) \%\)).
En la práctica normalmente \(\alpha^{\ast}\) no es conocida. Para estimarlo se puede realizar ajuste lineal de \(X\) sobre \(Y\) (a partir de los datos simulados \(X_{i}\) e \(Y_{i}\), \(1\leq i\leq n\)):
Si \(\hat{x}=\hat{\beta}_{0}+\hat{\beta}_{1}y\) es la recta ajustada, con \(\hat{\beta}_{1} = \dfrac{S_{XY}}{S_{Y}^{2}}\) y \(\hat{\beta}_{0} = \overline{X}-\hat{\beta}_{1}\overline{Y}\), la estimación sería: \[\hat{\alpha}^{\ast}=-\hat{\beta}_{1}\]
Adicionalmente, para aproximar \(\theta\): \[\begin{aligned} \hat{\theta} & =\overline{X}^{\ast}=\overline{X}-\hat{\beta}_{1}\left( \overline{Y}-\mu_{Y}\right) \\ & =\hat{\beta}_{0}+\hat{\beta}_{1}\mu_{Y} \end{aligned}\]
Si \(\mu_{Y}=0\Rightarrow \hat{\theta}=\overline{X}^{\ast}=\hat{\beta}_{0}\).
Ejemplo 8.4 (Integración Monte Carlo con variables de control)
Continuando con los ejemplos 8.1 y 8.3, aproximaremos la integral empleando la variable \(U\sim\mathcal{U}(0,2)\) para controlar la variable \(e^{U}\).
Se trata de calcular la media de \(exp(\mathcal{U}(a,b))\):
a <- 0; b <- 2
teor <- (exp(b)-exp(a))/(b-a)
teor## [1] 3.1945Aproximación clásica por simulación:
set.seed(54321)
nsim <- 1000
u <- runif(nsim, a, b)
expu <- exp(u)
mean(expu) ## [1] 3.1821Con variable control:
plot(u, expu)
reg <- lm(expu ~ u)$coef
abline(reg, col='blue')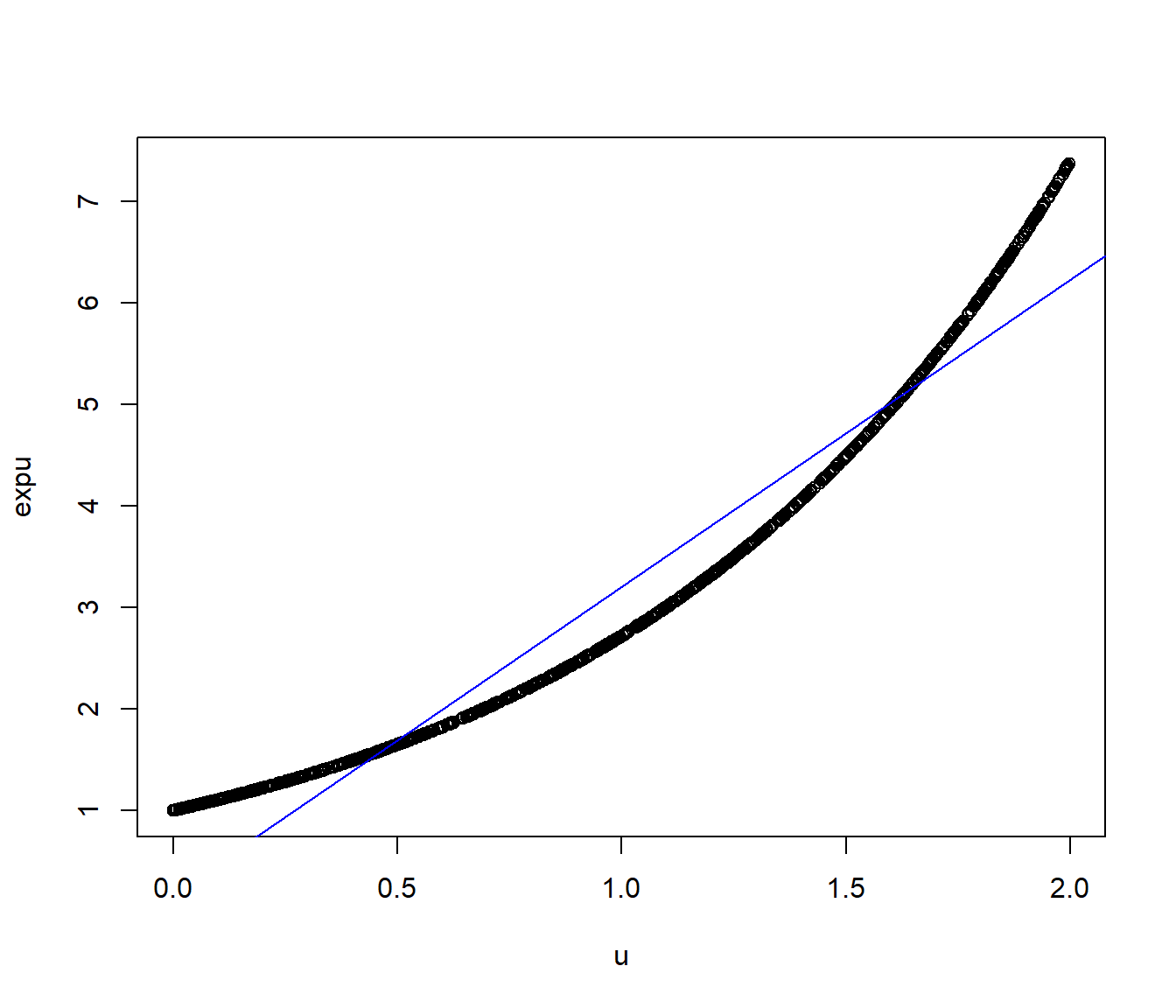
# summary(lm(expu ~ u)) # R-squared: 0.9392
reg[1]+reg[2] # Coincidirá con la solución mean(expuc)## (Intercept)
## 3.2049Lo siguiente ya no sería necesario:
expuc <- expu - reg[2]*(u-1)
mean(expuc) ## [1] 3.2049Estimación del porcentaje de reducción en la varianza:
100*(var(expu)-var(expuc))/var(expu)## [1] 93.916