D.3 Capítulo 5 Simulación de variables discretas

D.3.1 Ejercicio 5.1

Enunciado 5.1 (Simulación de una distribución mixta mediante el método de inversión generalizado):

Consideramos la variable aleatoria con función de distribución dada por: \[F(x)=\left\{ \begin{array} [c]{cl}0 & \mbox{si $x<0$}\\ \frac{x}{2}+\frac{1}{10} & \mbox{si $x\in[0,\frac{1}{5})$}\\ x+\frac{1}{10} & \mbox{si $x\in[\frac{1}{5},\frac{9}{10}]$}\\ 1 & \mbox{en otro caso} \end{array} \right.\]

Esta función está implementada en el siguiente código:

fdistr <- function(x) {
ifelse(x < 0, 0,
    ifelse(x < 1/5, x/2 + 1/10,
        ifelse(x <= 9/10, x + 1/10, 1) ) )
}

Como es una función vectorial podemos emplear curve() para representarla:

curve(fdistr, from = -0.1, to = 1.1, type = 's', main = '')
abline(h = c(1/10, 2/10, 3/10), lty = 2) # Discontinuidades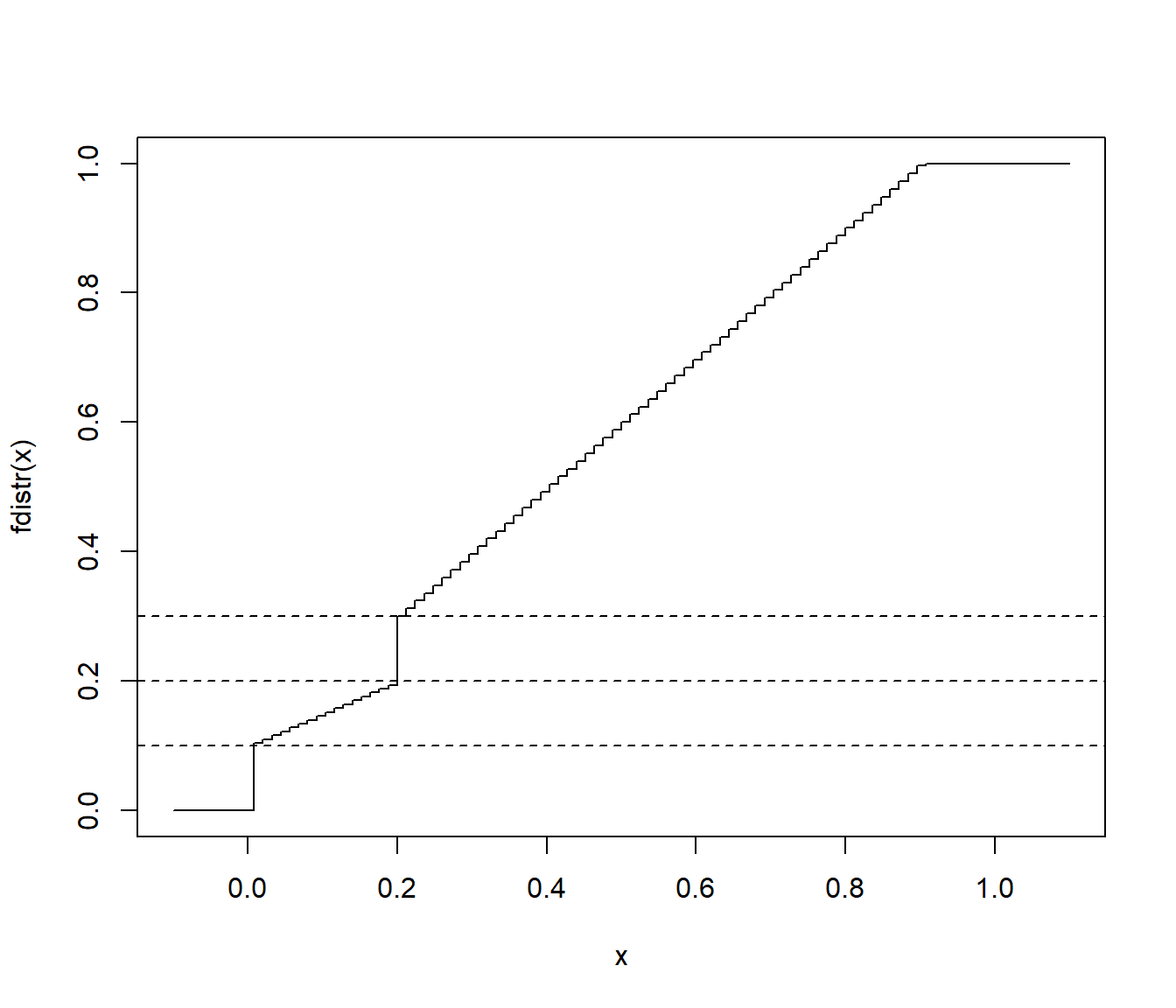
Función de distribución mixta (con discontinuidades en 0 y 1/5).

Figura D.4: Función de distribución mixta (con discontinuidades en 0 y 1/5).

Nota: Esta variable toma los valores 0 y 1/5 con probabilidad 1/10.

  1. Diseñar un algoritmo basado en el método de inversión generalizado para generar observaciones de esta variable.

  2. Implementar el algoritmo en una función que permita generar \(nsim\) valores de esta variable.

  1. El algoritmo general es siempre el mismo. Empleando la función cuantil: \[Q\left( u\right) = \inf \left\{ x\in \mathbb{R}:F\left( x\right) \geq u\right\},\] el algoritmo sería:

    1. Generar \(U\sim \mathcal{U}\left( 0,1\right)\)

    2. Devolver \(X=Q\left( U\right)\)

    En este caso concreto:

    1. Generar \(U\sim \mathcal{U}\left( 0,1\right)\)

    2. Si \(U < \frac{1}{10}\) devolver \(X = 0\)

    3. En caso contrario, si \(U < \frac{2}{10}\) devolver \(X = 2(U - \frac{1}{10})\)

    4. En caso contrario, si \(U < \frac{3}{10}\) devolver \(X = \frac{2}{10}\)

    5. En caso contrario devolver \(X = U - \frac{1}{10}\)

  2. El algoritmo de simulación se puede implementar a partir de la función cuantil (vectorial):

    # Función cuantil:
fquant <- function(u) 
  ifelse(u < 1/10, 0,
         ifelse(u < 2/10, 2*(u - 1/10),
                ifelse(u < 3/10, 1/5, u - 1/10) ) )
# Función para generar nsim valores:
rx <- function(nsim) fquant(runif(nsim))

    Ejemplo:

    set.seed(1)
nsim <- 10^4
system.time(simx <- rx(nsim))
    ##    user  system elapsed 
##       0       0       0
    hist(simx, breaks = "FD", freq = FALSE)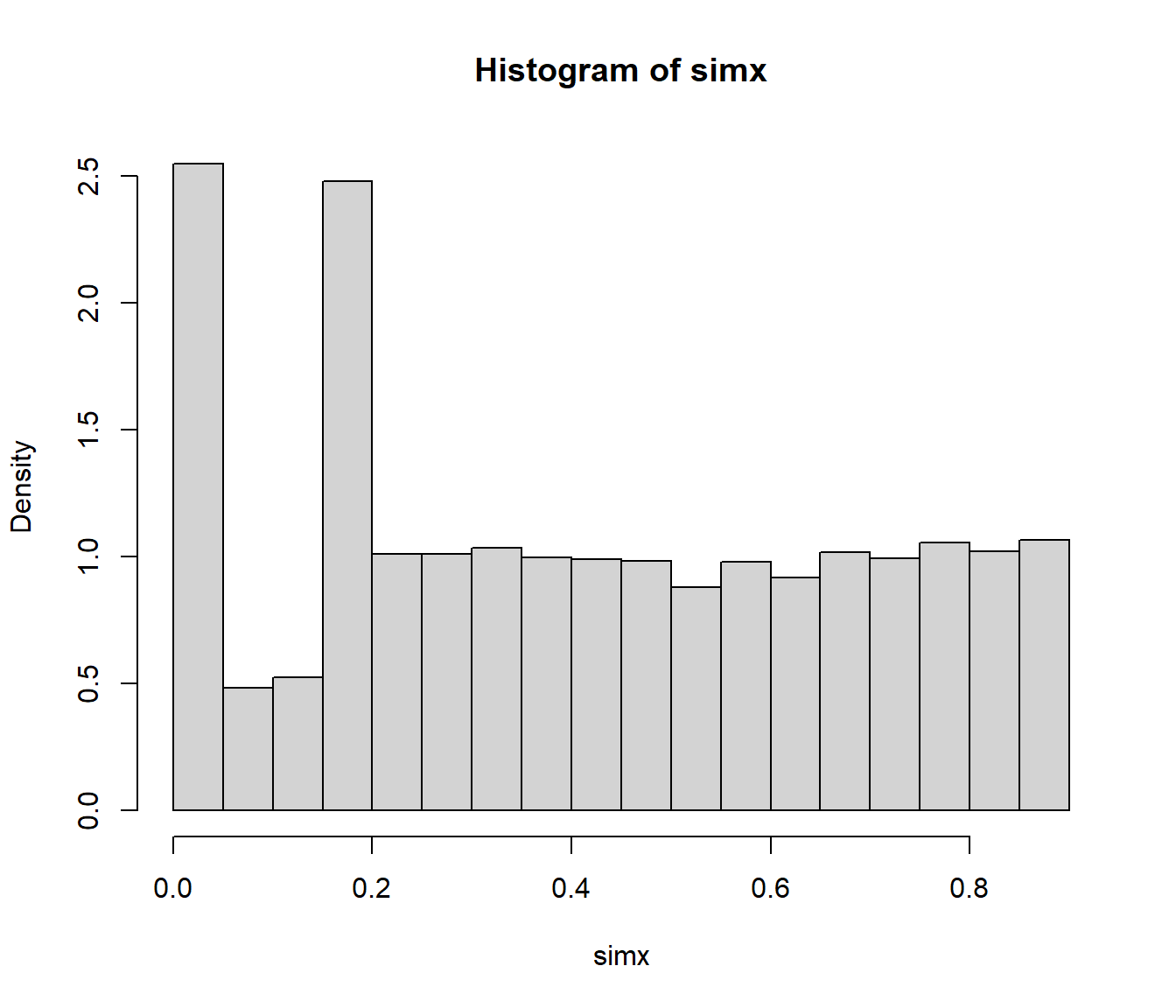

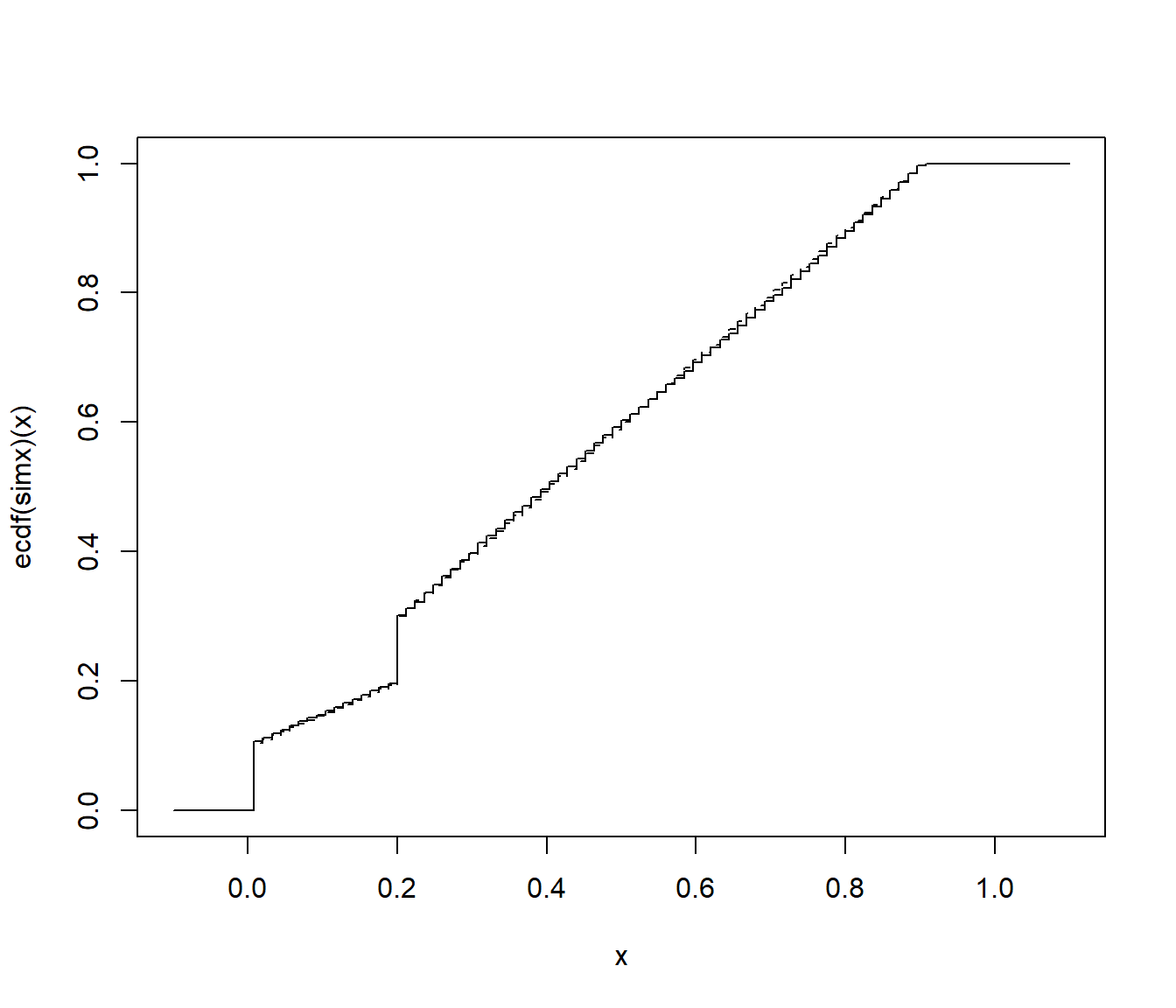
    En este caso como no es una variable absolutamente continua mejor emplear la función de distribución para compararla con la teórica:

    curve(ecdf(simx)(x), from= -0.1, to = 1.1, type = "s")
curve(fdistr(x), type = "s", lty = 2, add = TRUE)