3.1 Convergencia

Supongamos que estamos interesados en aproximar la media teórica \(\mu = E\left( X\right)\) a partir de una secuencia i.i.d. \(X_{1}\), \(X_{2}\), \(\ldots\), \(X_{n}\) obtenida mediante simulación, utilizando para ello la media muestral \(\bar{X}_{n}\). Una justificación teórica de la validez de esta aproximación es la ley (débil10) de los grandes números:

Teorema 3.1 (Ley débil de los grandes números; Khintchine, 1928)
Si \(X_{1}\), \(X_{2}\), \(\ldots\) es una secuencia de variables aleatorias independientes e idénticamente distribuidas con media finita \(E\left( X_{i}\right) =\mu\) (i.e. \(E\left( \left\vert X_{i} \right\vert \right) < \infty\)) entonces \(\overline{X}_{n}=\left( X_{1}+\ldots +X_{n}\right) /n\) converge en probabilidad a \(\mu\): \[\overline{X}_{n}\ \overset{p}{ \longrightarrow }\ \mu\] Es decir, para cualquier \(\varepsilon >0\): \[\lim\limits_{n\rightarrow \infty }P\left( \left\vert \overline{X}_{n}-\mu \right\vert <\varepsilon \right) = 1.\]

Ejemplo 3.1 (Aproximación de una probabilidad)

Simulamos una variable aleatoria \(X\) con distribución de Bernoulli de parámetro \(p=0.5\):

p <- 0.5
set.seed(1)
nsim <- 10000 # nsim <- 100
rx <- runif(nsim) < p # rbinom(nsim, size = 1, prob = p)

La aproximación por simulación de \(E(X) = p\) será:

mean(rx) 
## [1] 0.5047

Podemos generar un gráfico con la evolución de la aproximación:

plot(cumsum(rx)/1:nsim, type = "l", lwd = 2, xlab = "Número de generaciones", 
     ylab = "Proporción muestral", ylim = c(0, 1))
abline(h = mean(rx), lty = 2)
# valor teórico
abline(h = p)
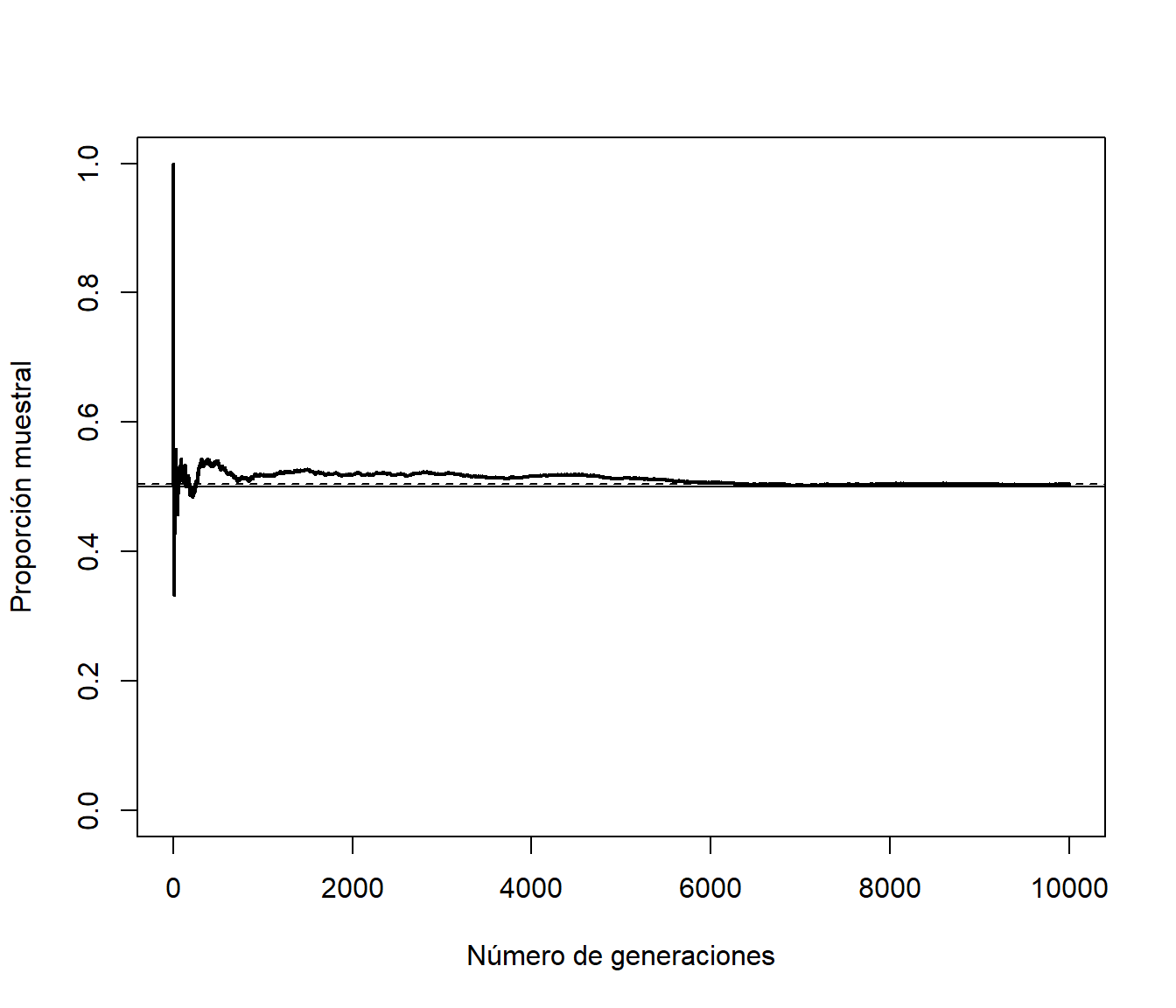
Aproximación de la proporción en función del número de generaciones.

Figura 3.1: Aproximación de la proporción en función del número de generaciones.

3.1.1 Detección de problemas de convergencia

En la ley débil se requiere como condición suficiente que \(E\left( \left\vert X_{i} \right\vert \right) < \infty\), en caso contrario la media muestral puede no converger a una constante. Un ejemplo conocido es la distribución de Cauchy:

set.seed(1)
nsim <- 10000
rx <- rcauchy(nsim) # rx <- rt(nsim, df = 2)
plot(cumsum(rx)/1:nsim, type = "l", lwd = 2, 
     xlab = "Número de generaciones", ylab = "Media muestral")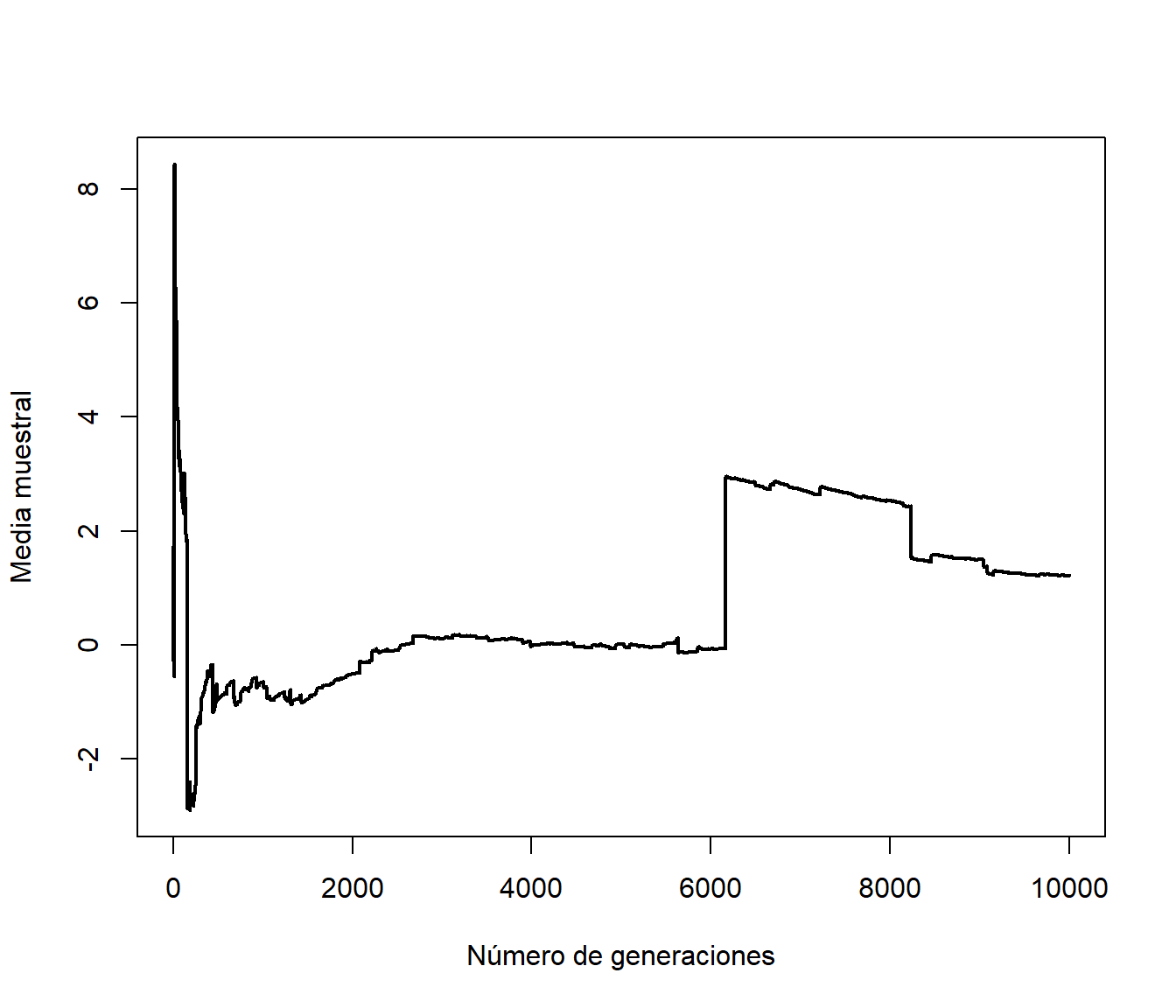
Evolución de la media muestral de una distribución de Cauchy en función del número de generaciones.

Figura 3.2: Evolución de la media muestral de una distribución de Cauchy en función del número de generaciones.

Como conclusión, para detectar problemas de convergencia es especialmente recomendable representar la evolución de la aproximación de la característica de interés (sobre el número de generaciones), además de realizar otros análisis descriptivos de las simulaciones. Por ejemplo, en este caso podemos observar los valores que producen estos saltos mediante un gráfico de cajas:

boxplot(rx)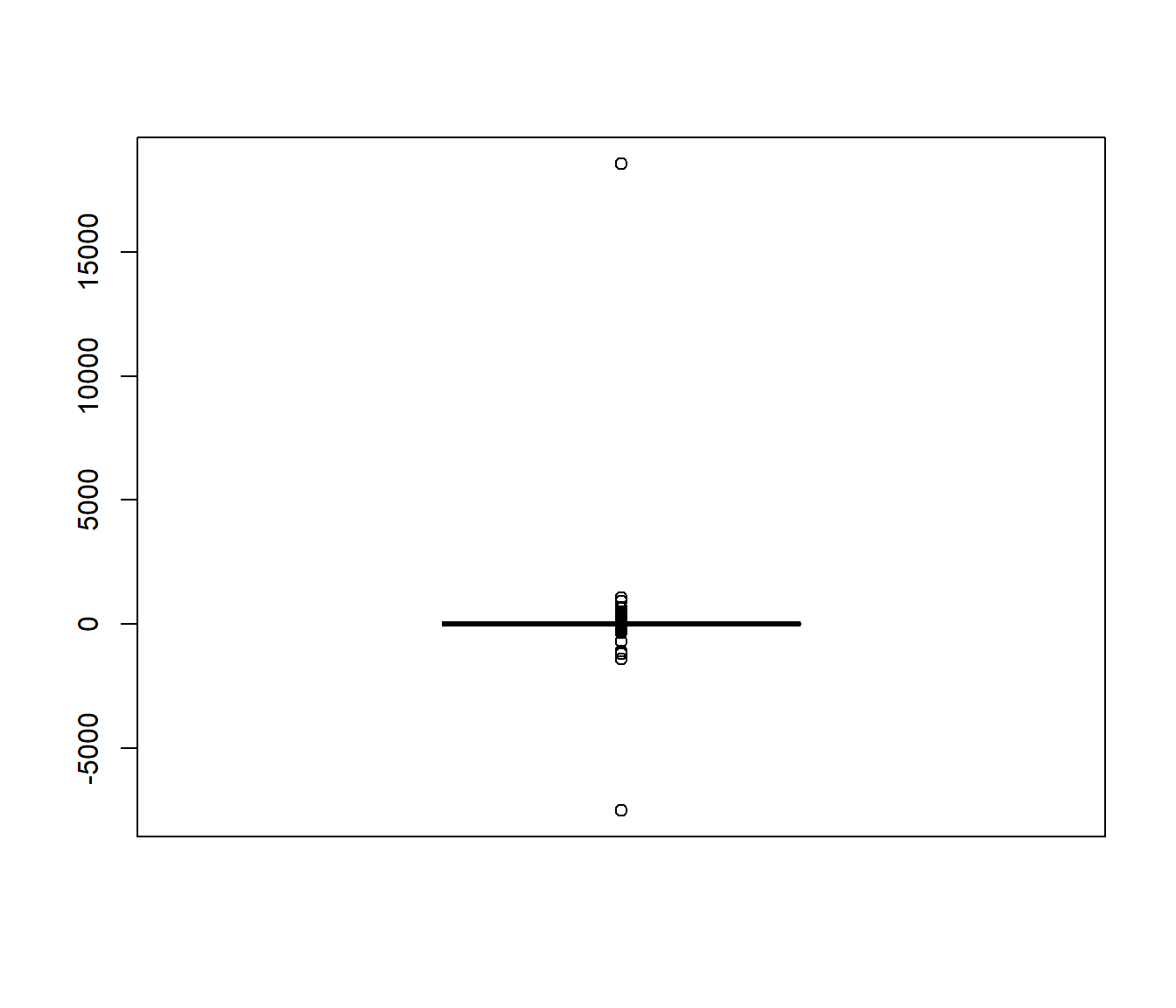
Gráfico de cajas de 10000 generaciones de una distribución de Cauchy.

Figura 3.3: Gráfico de cajas de 10000 generaciones de una distribución de Cauchy.

3.1.2 Precisión

Una forma de medir la precisión de un estimador es utilizando su varianza, o también su desviación típica que recibe el nombre de error estándar. En el caso de la media muestral \(\overline{X}_{n}\), suponiendo además que \(Var\left( X_{i}\right) = \sigma^{2}<\infty\), un estimador insesgado de \(Var\left( \overline{X}_{n}\right) =\sigma ^{2}/n\) es: \[\widehat{Var}\left( \overline{X}_{n}\right) = \frac{\widehat{S}_n^{2}}{n}\] donde: \[\widehat{S}_{n}^{2}=\dfrac{1}{n-1}\sum\limits_{i=1}^{n}\left( X_{i}- \overline{X}\right) ^{2}\] es la cuasi-varianza muestral11.

Los valores obtenidos servirían como medidas básicas de la precisión de la aproximación, aunque su principal aplicación es la construcción de intervalos de confianza. Si se endurecen las suposiciones de la ley débil de los grandes números (Teorema 3.1), exigiendo la existencia de varianza finita (\(E\left( X_{i}^2 \right) < \infty\)), se dispone de un resultado más preciso sobre las variaciones de la aproximación por simulación en torno al límite teórico.

Teorema 3.2 (central del límite CLT)

Si \(X_{1}\), \(X_{2}\), \(\ldots\) es una secuencia de variables aleatorias independientes e idénticamente distribuidas con \(E\left( X_{i}\right) =\mu\) y \(Var\left( X_{i}\right) = \sigma ^{2}<\infty\), entonces la media muestral estandarizada converge en distribución a una normal estándar: \[Z_{n}=\frac{\overline{X}_{n}-\mu }{\frac{\sigma }{\sqrt{n}}} \overset{d}{ \longrightarrow } N(0,1).\] Es decir, \(\lim\limits_{n\rightarrow \infty }F_{Z_{n}}(z)=\Phi (z)\).

Por tanto, un intervalo de confianza asintótico para \(\mu\) es: \[IC_{1-\alpha }(\mu ) = \left( \overline{X}_{n} - z_{1-\alpha /2}\dfrac{\widehat{S}_{n}}{\sqrt{n}},\ \overline{X}_n+z_{1-\alpha /2}\dfrac{\widehat{S}_{n}}{\sqrt{n}} \right).\]

También podemos utilizar el error máximo (con nivel de confianza \(1-\alpha\)) de la estimación \(z_{1-\alpha /2}\dfrac{\widehat{S}_{n}}{\sqrt{n}}\) como medida de su precisión.

El CLT es un resultado asintótico. En la práctica la convergencia es aleatoria, ya que depende de la muestra simulada (las generaciones pseudoaleatorias). Además, la convergencia puede considerarse lenta, en el sentido de que, por ejemplo, para doblar la precisión (disminuir el error a la mitad), necesitaríamos un número de generaciones cuatro veces mayor (Ver Sección 3.2). Pero una ventaja es que este error no depende del número de dimensiones (en el caso multidimensional puede ser mucho más rápida que otras alternativas numéricas; ver Apéndice B).

Ejemplo 3.2 (Aproximación de la media de una distribución normal)

Como ejemplo simulamos valores de una normal estándar:

xsd <- 1
xmed <- 0
set.seed(1)
nsim <- 1000
rx <- rnorm(nsim, xmed, xsd)

La aproximación por simulación de la media será:

mean(rx)
## [1] -0.01164814

Como medida de la precisión de la aproximación podemos utilizar el error máximo:

2*sd(rx)/sqrt(nsim)
## [1] 0.06545382

(es habitual emplear 2 en lugar de 1.96, lo que se correspondería con \(1 - \alpha = 0.9545\) en el caso de normalidad). Podemos añadir también los correspondientes intervalos de confianza al gráfico de convergencia:

n <- 1:nsim
est <- cumsum(rx)/n
# (cumsum(rx^2) - n*est^2)/(n-1) # Cuasi-varianzas muestrales
esterr <- sqrt((cumsum(rx^2)/n - est^2)/(n-1)) # Errores estándar de la media
plot(est, type = "l", lwd = 2, xlab = "Número de generaciones", 
     ylab = "Media y rango de error", ylim = c(-1, 1))
abline(h = est[nsim], lty=2)
lines(est + 2*esterr, lty=3)
lines(est - 2*esterr, lty=3)
abline(h = xmed)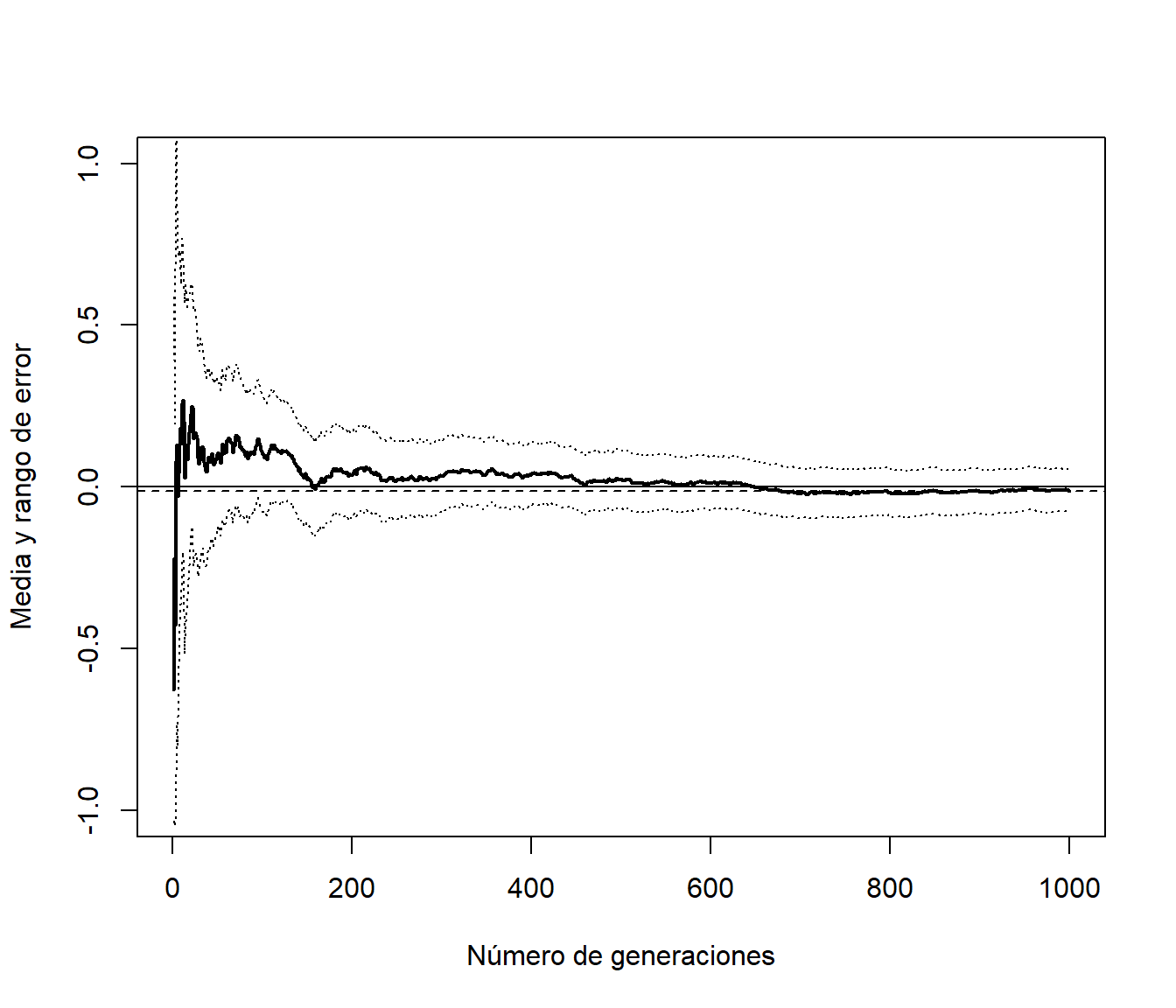
Gráfico de convergencia incluyendo el error de la aproximación.

Figura 3.4: Gráfico de convergencia incluyendo el error de la aproximación.

Podemos generar este gráfico empleando la función conv.plot() (o mc.plot()) del paquete simres (fichero mc.plot.R).

  1. La ley fuerte establece la convergencia casi segura.↩︎

  2. Esto sería también válido para el caso de una proporción, donde \(E(X) = p\), \(Var(X) = p(1-p)\) y \(\hat{p}_{n} = \overline{X}_{n}\), obteniéndose que: \[\widehat{Var}\left( \hat{p}_{n}\right) = \frac{\widehat{S}_n^{2}}{n} = \frac{\hat{p}_{n}(1-\hat{p}_{n})}{n-1},\] aunque lo más habitual es emplear: \[\frac{S_n^{2}}{n} = \frac{\hat{p}_{n}(1-\hat{p}_{n})}{n},\] donde \(S_n^{2}\) es la varianza muestral. Hay que tener en cuenta que en simulación el número de generaciones es normalmente grande y en la práctica no va haber diferencias apreciables.↩︎