5.6 Métodos específicos para generación de distribuciones notables
Los comentarios al principio de la Sección 4.5 para el caso de variables continuas serían válidos también para distribuciones notables discretas.
Entre los distintos métodos disponibles para la generación de las distribuciones discretas más conocidas podríamos destacar el de la distribución binomial negativa mediante el método de composición (Sección 4.4).
La distribución binomial negativa, \(\mathcal{BN}(r, p)\), puede interpretarse como el número de fracasos antes del \(r\)-ésimo éxito26 y su función de masa de probabilidad es \[P(X = i) = \binom{i+r-1}i p^r (1-p)^i \text{, para }i=0,1,\ldots\]
A partir de la propiedad (ver e.g. Devroye, 1986, pp. 488-489) \[X|_{Y} \sim \mathcal{Pois}\left( Y\right) \text{, }Y \sim \mathcal{Gamma} \left( r, \frac{p}{1-p}\right) \Rightarrow X \sim \mathcal{BN}(r, p)\] se puede deducir el siguiente método específico de simulación.
Algoritmo 5.8 (distribución binomial negativa)
Simular \(L \sim \mathcal{Gamma}\left( r, \frac{p}{1-p} \right)\).
Simular \(X \sim \mathcal{Pois} \left( L\right)\).
Devolver \(X\).
La función rnbinom() implementa este algoritmo internamente27,
y podemos imitar su funcionamiento con el siguiente código:
r <- 5
p <- 0.5
nsim <- 10^4
set.seed(1)
lambda <- rgamma(nsim, r, p/(1-p))
rx <- rpois(nsim, lambda)Como comprobación de que el algoritmo está bien implementado (es un método exacto de simulación), comparamos las aproximaciones de las probabilidades de los valores generados con los valores teóricos:
res <- table(rx)/nsim
plot(res, ylab = "frecuencia relativa", xlab = "valores")
x <- 0:max(as.numeric(names(res)))
points(x, dnbinom(x, r, p), pch = 4, col = "blue") # Comparación teórica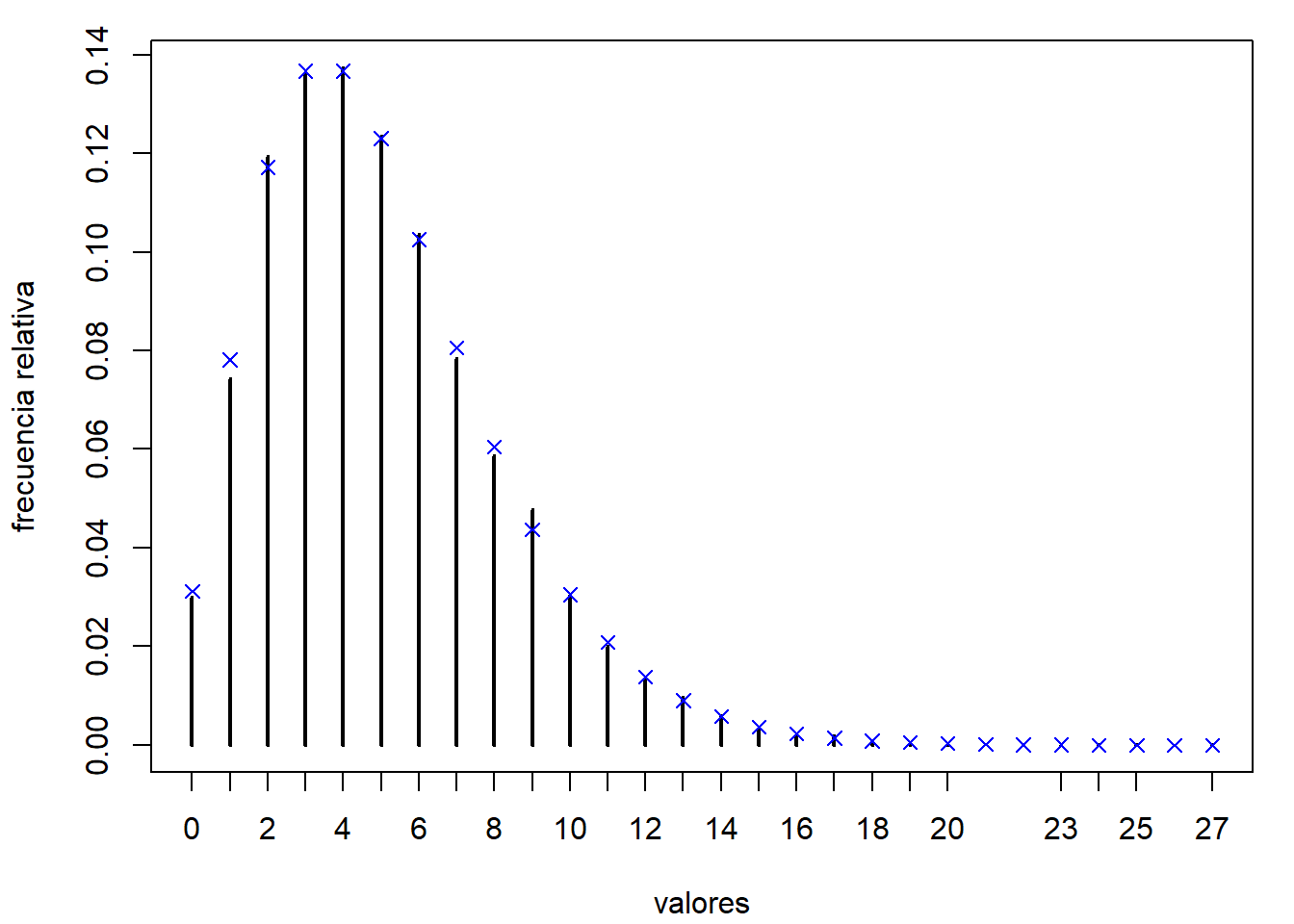
Figura 5.8: Comparación de las frecuencias relativas de los valores generados de la distribución binomial negativa, mediante composición, con las probabilidades teóricas.
Esta propiedad es el motivo de que a la distribución geométrica se la denomine también distribución Gamma-Poisson. Empleando una aproximación similar podríamos generar otras distribuciones, como la Beta-Binomial, empleadas habitualmente en inferencia bayesiana.
Bibliografía
La distribución binomial negativa es una generalización de la geométrica y, debido a su reproductividad en el parámetro \(r\), podría simularse como suma de \(r\) variables geométricas. Sin embargo, este algoritmo puede ser muy costoso en tiempo de computación si \(r\) es elevado.↩︎