5.5 Otros métodos
Muchos de los métodos descritos en el Capítulo 4 para variables continuas son directamente aplicables al caso discreto:
Aceptación-Rechazo (Sección 4.2): En principio habría que considerar una variable auxiliar discreta con el mismo soporte, pero también hay modificaciones para variables auxiliares continuas.
Método de composición (Sección 4.4): es uno de los más empleados, por ejemplo en el método de Alias (Sección 5.3) y para simular la distribución binomial negativa (Sección 5.6).
Hay otros métodos que tratan de reducir el número medio de comparaciones de la búsqueda secuencial, por ejemplo los árboles (binarios) de Huffman (e.g. Cao, 2002, Sección 4.2). Estos métodos son muy poco eficientes para simular variables discretas pero pueden resultar de utilidad para diseñar experimentos de simulación más complejos (la idea es la misma, preocuparse principalmente por los sucesos más probables).
En ocasiones el método de la transformación cuantil puede acelerarse computacionalmente porque, mediante cálculos directos, es posible encontrar el valor de la función cuantil en cualquier \(U\), evitando el bucle de búsqueda. Normalmente se realiza mediante truncamiento de una distribución continua auxiliar.
Ejemplo 5.6 (distribución geométrica)
La función de masa de probabilidad de una distribución geométrica, \(X =\) “número de fracasos antes del primer éxito” \(\sim \mathcal{Geom}(p)\), es: \[P(X = i) = p(1-p)^i \text{, } i = 0, 1, \ldots\] siendo \(p\) la probabilidad de éxito.
Esta distribución podría simularse fácilmente a partir de su definición aunque el algoritmo resultante puede ser muy poco eficiente (especialmente si \(p\) es pequeña). Un algoritmo más eficiente, equivalente a emplear la expresión explícita de su función cuantil (e.g. Cao Abad, 2002, sec. 4.1.2), consiste en truncar generaciones de una variable aleatoria auxiliar con distribución exponencial.
Si \(T \sim \mathcal{Exp}(\lambda)\), con función de distribución \(G(t) = 1-e^{-\lambda t}\) si \(t \geq 0\), se tiene que25: \[\begin{aligned} P\left( \left\lfloor T \right\rfloor = i \right) & = P(i \leq T < i + 1 ) = G(i + 1) - G(i) \\ & = 1-e^{-\lambda (i+1)} - \left(1-e^{-\lambda i}\right) = e^{-\lambda i} - e^{-\lambda (i+1)}\\ & = e^{-\lambda i }\left(1-e^{-\lambda}\right) = \left(1-e^{-\lambda}\right) \left(e^{-\lambda}\right)^i \\ & = p(1-p)^i, \end{aligned}\] tomando \(p=1-e^{-\lambda}\). De donde se obtendría el algoritmo:
Algoritmo 5.7 (distribución geométrica mediante truncamiento)
Hacer \(\lambda = -\ln(1 - p)\).
Generar \(U \sim \mathcal{U}(0, 1)\).
Hacer \(T = -\frac{\ln U}{\lambda}\).
Devolver \(X = \left\lfloor T \right\rfloor\).
El siguiente código emplea una versión vectorizada de este algoritmo para generar nsim valores de una distribución geométrica de parámetro p:
p <- 0.3
nsim <- 10^4
set.seed(1)
rx <- floor(rexp(nsim, rate = -log(1 - p)))Como comprobación de que el algoritmo está bien implementado (es un método exacto de simulación), comparamos las aproximaciones de las probabilidades de los valores generados con los valores teóricos:
res <- table(rx)/nsim
plot(res, ylab = "frecuencia relativa", xlab = "valores")
x <- 0:max(as.numeric(names(res)))
points(x, dnbinom(x, 1, p), pch = 4, col = "blue") # Comparación teórica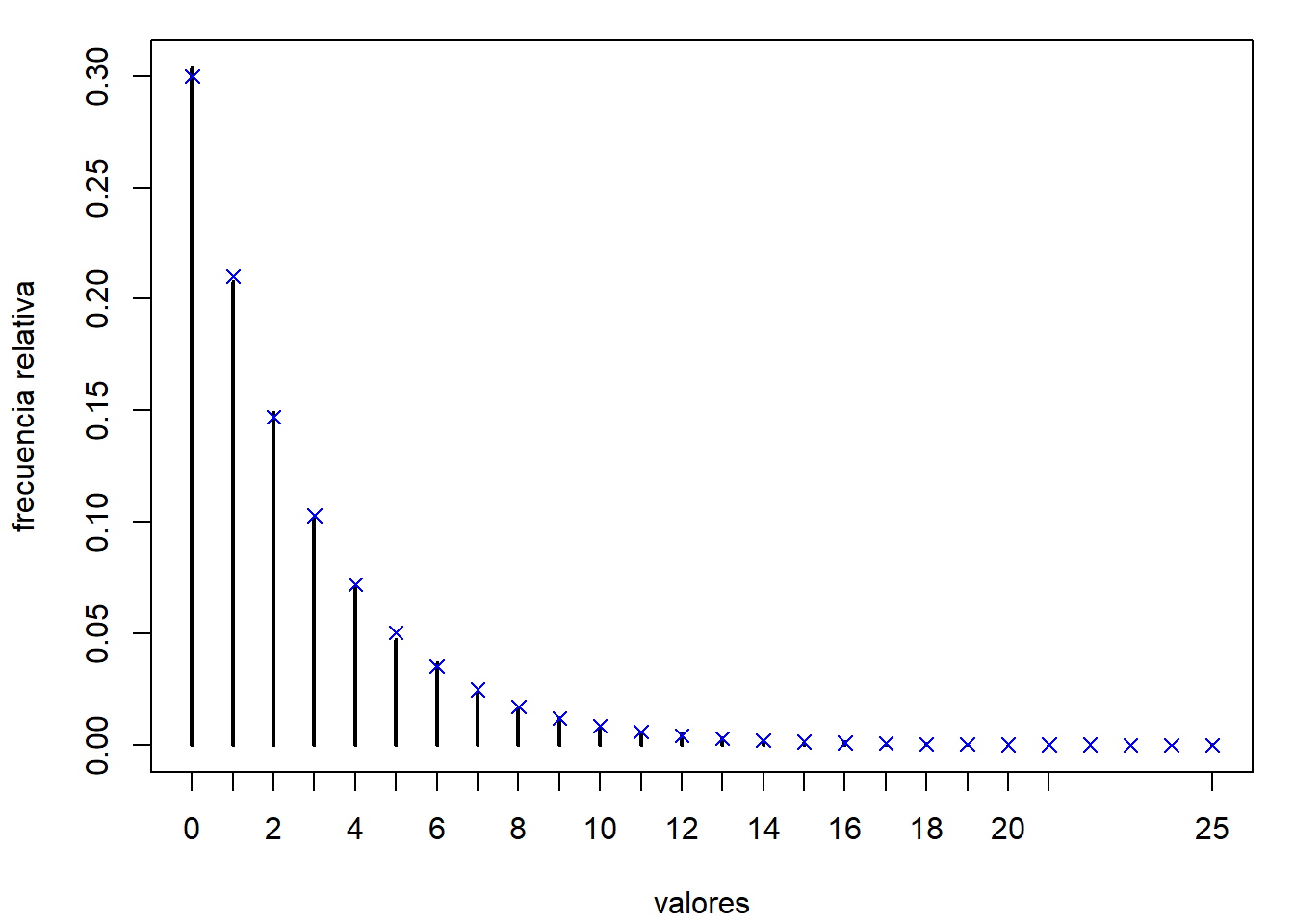
Figura 5.7: Comparación de las frecuencias relativas de los valores generados de la distribución geométrica, mediante truncamiento, con las probabilidades teóricas.
Bibliografía
Es equivalente a considerar \(\left\lceil T \right\rceil -1\) ya que la distribución exponencial es absolutamente continua.↩︎