2.1 Generadores congruenciales lineales

En los generadores congruenciales lineales se considera una combinación lineal de los últimos \(k\) enteros generados y se calcula su resto al dividir por un entero fijo \(m\). En el método congruencial simple (de orden \(k = 1\)), partiendo de una semilla inicial \(x_0\), el algoritmo secuencial es el siguiente: \[\begin{aligned} x_{i} & = (ax_{i-1}+c) \bmod m \\ u_{i} & = \dfrac{x_{i}}{m} \\ i & =1,2,\ldots \end{aligned}\] donde \(a\) (multiplicador), \(c\) (incremento) y \(m\) (módulo) son enteros positivos⁶ fijados de antemano (los parámetros de este generador). Si \(c=0\) el generador se denomina congruencial multiplicativo (Lehmer, 1951) y en caso contrario se dice que es mixto (Rotenburg, 1960).

Obviamente los parámetros y la semilla determinan los valores generados, que también se pueden obtener de forma no recursiva: \[x_{i}=\left( a^{i}x_0+c\frac{a^{i}-1}{a-1}\right) \bmod m\]

Este método está implementado⁷ en la función rlcg() del paquete simres, imitando el funcionamiento del generador uniforme de R (ver también simres::rng(); fichero rng.R):

simres::rlcg

## function(n, seed = as.numeric(Sys.time()), a = 7^5, c = 0, m = 2^31 - 1) {
##   u <- numeric(n)
##   for(i in 1:n) {
##     seed <- (a * seed + c) %% m
##     u[i] <- seed/m # (seed + 1)/(m + 1)
##   }
##   # Almacenar semilla y parámetros
##   assign(".rng", list(seed = seed, type = "lcg",
##           parameters = list(a = a, c = c, m = m)), envir = globalenv())
##   # .rng <<- list(seed = seed, type = "lcg", parameters = list(a = a, c = c, m = m))
##   # Para continuar con semilla y parámetros:
##   #   with(.rng, rlcg(n, seed, parameters$a, parameters$c, parameters$m))
##   # Devolver valores
##   return(u)
## }
## <bytecode: 0x00000239854a5308>
## <environment: namespace:simres>

Ejemplos de parámetros:

\(c=0\), \(a=2^{16}+3=65539\) y \(m=2^{31}\), generador RANDU de IBM (no recomendable como veremos más adelante).
\(c=0\), \(a=7^{5}=16807\) y \(m=2^{31}-1\) (primo de Mersenne), Park y Miller (1988) minimal standar, empleado por las librerías IMSL y NAG.
\(c=0\), \(a=48271\) y \(m=2^{31}-1\) actualización del minimal standar propuesta por Park, Miller y Stockmeyer (1993).

A pesar de su simplicidad, una adecuada elección de los parámetros permite obtener de manera eficiente secuencias de números “aparentemente” i.i.d. \(\mathcal{U}(0,1)\). Durante los primeros años, el procedimiento habitual consistía en escoger \(m\) de forma que se pudiera realizar eficientemente la operación del módulo, aprovechando la arquitectura del ordenador (por ejemplo \(m = 2^{31}\) si se emplean enteros con signo de 32 bits). Posteriormente se seleccionaban \(c\) y \(a\) de forma que el período \(p\) fuese lo más largo posible (o suficientemente largo), empleando los resultados mostrados a continuación.

Teorema 2.1 (Hull y Dobell, 1962)
Un generador congruencial tiene período máximo (\(p=m\)) si y solo si:

\(c\) y \(m\) son primos relativos (i.e. \(m.c.d.(c, m) = 1\)).
\(a-1\) es múltiplo de todos los factores primos de \(m\) (i.e. \(a \equiv 1 \bmod q\), para todo \(q\) factor primo de \(m\)).
Si \(m\) es múltiplo de \(4\), entonces \(a-1\) también lo ha de ser (i.e. \(m \equiv 0 \bmod 4\Rightarrow a \equiv 1 \bmod 4\)).

Algunas consecuencias:

Si \(m\) primo, \(p=m\) si y solo si \(a=1\).
Un generador multiplicativo no cumple la condición 1 (\(m.c.d.(0, m)=m\)).

Teorema 2.2
Un generador multiplicativo tiene período máximo (\(p=m-1\)) si:

\(m\) es primo.
\(a\) es una raiz primitiva de \(m\) (i.e. el menor entero \(q\) tal que \(a^{q}=1 \bmod m\) es \(q=m-1\)).

Sin embargo, además de preocuparse de la longitud del ciclo, sería mucho más importante que las secuencias generadas se comporten de forma similar a muestras aleatorias simple de una \(\mathcal{U}(0,1)\). Uno de los principales problemas con este tipo de generadores (y con muchos otros) es que los valores generados pueden mostrar una estructura reticular. Este es el caso del generador RANDU de IBM muy empleado en la década de los 70 y que muestra una clara estructura reticular cuando se consideran más de dos dimensiones (aunque ya se detectó este problema en 1963 se siguió utilizando hasta los 90). Para ilustrar este problema podríamos emplear el conjunto de datos randu del paquete base datasets que contiene 400 tripletas de números sucesivos generados con la implementación de VAX/VMS 1.5 (de 1977, y que no se corrigió hasta la versión 2.0 de 1980). Aunque también podemos emplear el siguiente código⁸ (ver Figura 2.1):

library(simres)
system.time(u <- rlcg(n = 9999, 
          seed = 543210, a = 2^16 + 3, c = 0, m = 2^31))

##    user  system elapsed 
##    0.00    0.00    0.02

# xyz <- matrix(u, ncol = 3, byrow = TRUE)
xyz <- stats::embed(u, 3)
library(plot3D)
# points3D(xyz[,1], xyz[,2], xyz[,3], colvar = NULL, phi = 60, 
#          theta = -50, pch = 21, cex = 0.2)
points3D(xyz[,3], xyz[,2], xyz[,1], colvar = NULL, phi = 60, 
         theta = -50, pch = 21, cex = 0.2)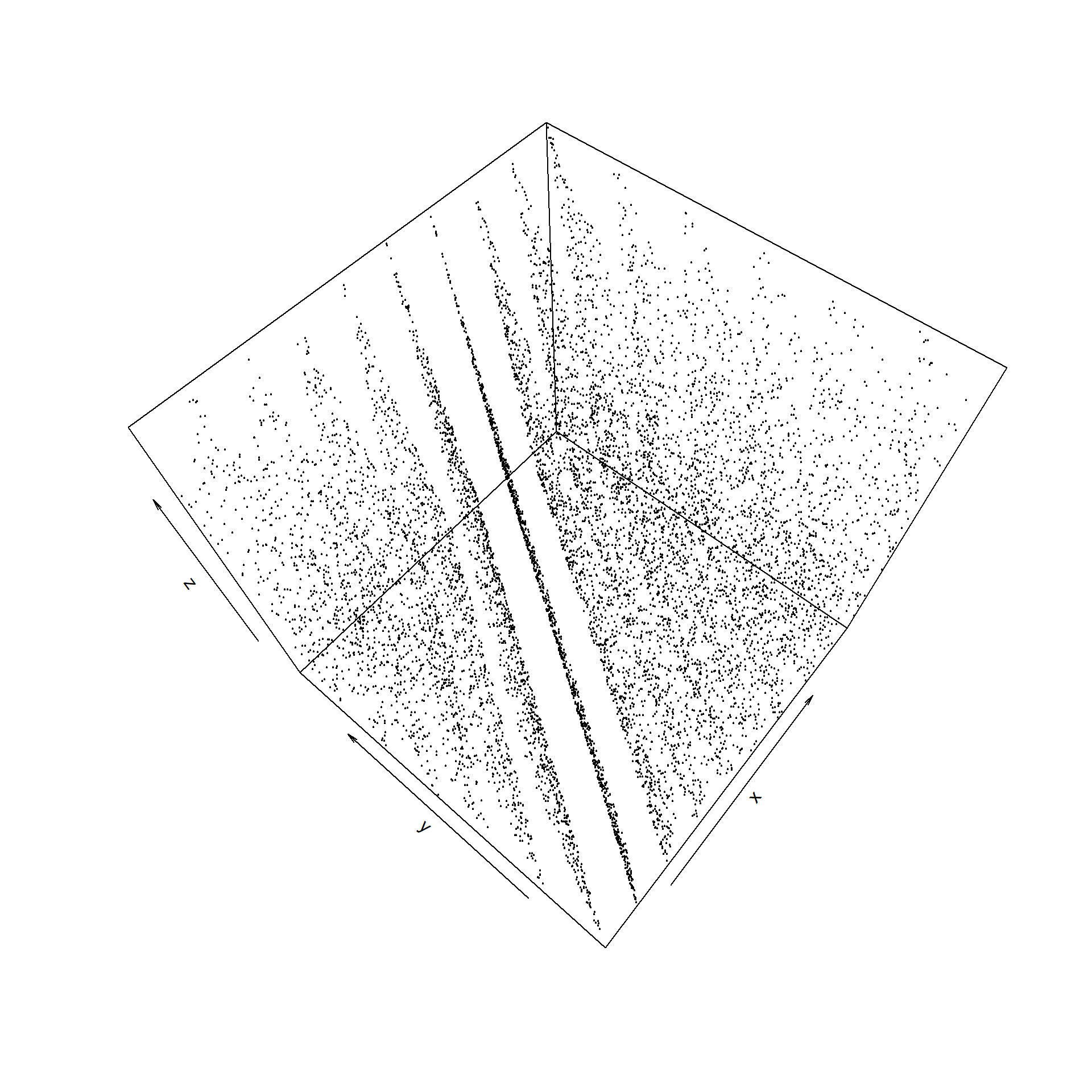

Figura 2.1: Grafico de dispersión de tripletas del generador RANDU de IBM (contenidas en 15 planos).

En general todos los generadores de este tipo van a presentar estructuras reticulares. Marsaglia (1968) demostró que las k-uplas de un generadores multiplicativo están contenidas en a lo sumo \(\left(k!m\right)^{1/k}\) hiperplanos paralelos (rtrunc((factorial(3)*2³¹⁾(1/3))` como máximo con \(k=3\) y \(m=2^{31}\)). Por tanto habría que seleccionar adecuadamente los parámetros del generador congruencial de forma que la estructura reticular sea imperceptible, teniendo en cuenta el número de datos que se pretende generar (por ejemplo de forma que la distancia mínima entre los puntos sea próxima a la esperada en teoría). Para más detalles sobre la estructura reticular ver por ejemplo Ripley (1987, Sección 2.7).

Se han propuesto diversas pruebas (ver Sección 2.3) para determinar si un generador tiene problemas de este tipo y se han realizado numerosos estudios para determinadas familias (e.g. Park y Miller, 1988, estudiaron los multiplicadores adecuados para \(m=2^{31}-1\)). En ciertos contextos muy exigentes (por ejemplo en criptografía), se recomienda considerar un “periodo de seguridad” \(\approx \sqrt{p}\) para evitar este tipo de problemas.

Aunque estos generadores tienen limitaciones en su capacidad para producir secuencias muy largas de números i.i.d. \(\mathcal{U}(0,1)\), son un elemento básico en generadores más avanzados (incluyendo el empleado por defecto en R) como veremos en la siguiente sección.

Ejemplo 2.1

Consideramos el generador congruencial, de ciclo máximo, definido por: \[\begin{aligned} x_{n+1} & =(5x_{n}+1)\ \bmod\ 512,\nonumber\\ u_{n+1} & =\frac{x_{n+1}}{512},\ n=0,1,\dots\nonumber \end{aligned}\]

Generar 500 valores de este generador, obtener el tiempo de CPU, representar su distribución mediante un histograma (en escala de densidades) y compararla con la densidad teórica.
```
set.rng(321, "lcg", a = 5, c = 1, m = 512)  # Establecer semilla y parámetros
nsim <- 500
system.time(u <- rng(nsim)) 
```
```
##    user  system elapsed 
##       0       0       0
```
```
hist(u, freq = FALSE)
abline(h = 1)                   # Densidad uniforme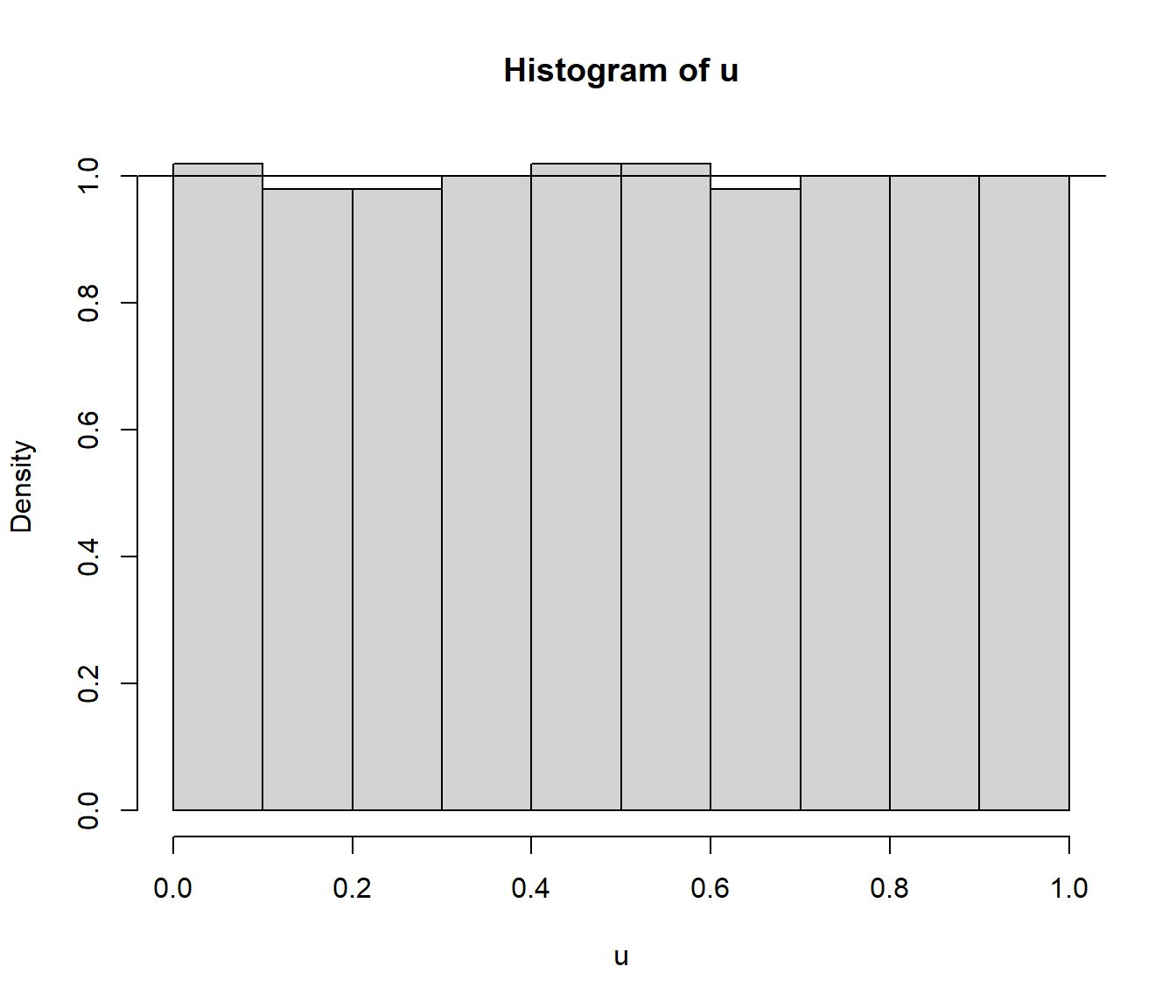
```
Figura 2.2: Histograma de los valores generados.

En este caso concreto la distribución de los valores generados es aparentemente más uniforme de lo que cabría esperar, lo que induciría a sospechar de la calidad de este generador (ver Ejemplo 2.2 en Sección 2.3).
Calcular la media de las simulaciones (mean) y compararla con la teórica.

La aproximación por simulación de la media teórica es:
```
mean(u)
```
```
## [1] 0.4999609
```
La media teórica es 0.5. Error absoluto \(3.90625\times 10^{-5}\).
Aproximar (mediante simulación) la probabilidad del intervalo \((0.4;0.8)\) y compararla con la teórica.

La probabilidad teórica es 0.8 - 0.4 = 0.4

La aproximación mediante simulación:
```
sum((0.4 < u) & (u < 0.8))/nsim
```
```
## [1] 0.402
```
```
mean((0.4 < u) & (u < 0.8))     # Alternativa
```
```
## [1] 0.402
```

Se supone además que \(a\), \(c\) y \(x_0\) son menores que \(m\), ya que, dadas las propiedades algebraicas de la suma y el producto en el conjunto de clases de resto módulo \(m\) (que es un anillo), cualquier otra elección de valores mayores o iguales que \(m\) tiene un equivalente verificando esta restricción.↩︎
Aunque de forma no muy eficiente. Para evitar problemas computacionales, se recomienda realizar el cálculo de los valores empleando el método de Schrage (ver Bratley et al., 1987; L’Ecuyer, 1988).↩︎
La función stats::embed(u, 3) devuelve una matriz en la que la fila i-ésima contiene los valores u[i+2], u[i+1] y u[i]. Además, en lugar de la función plot3D::points3D() se podría utilizar la función plot3d() del paquete rgl, y rotar la figura (pulsando con el ratón) para ver los hiperplanos rgl::plot3d(xyz).↩︎