5.1 Método de la transformación cuantil
Este método es una adaptación del método de inversión (válido para el caso continuo) a distribuciones discretas, por lo que también se denomina método de inversión generalizado. En este caso, la función de distribución es: \[F\left( x\right) =\sum_{x_{j}\leq x}p_{j},\] y la distribución de la variable aleatoria \(F\left( X\right)\) no es uniforme (es una variable aleatoria discreta que toma los valores \(F\left( x_{i} \right)\) con probabilidad \(p_{i}\), \(i=1,2,\ldots\)). Sin embargo, se puede generalizar el método de inversión a situaciones en las que \(F\) no es invertible considerando la función cuantil.
Se define la función cuantil o inversa generalizada de una función de distribución \(F\) como: \[Q\left( u\right) =\inf \left\{ x\in \mathbb{R}:F\left( x\right) \geq u\right\} ,\ \forall u\in \left( 0,1\right).\] Si \(F\) es invertible \(Q=F^{-1}\).
Teorema 5.1 (de inversión generalizada)
Si \(U\sim \mathcal{U}\left( 0,1\right)\), la variable aleatoria \(Q\left( U\right)\) tiene función de distribución \(F\).
Demostración. Bastaría ver que: \[Q\left( u\right) \leq x \Longleftrightarrow u\leq F(x).\]
Como \(F\) es monótona y por la definición de \(Q\): \[Q\left( u\right) \leq x \Rightarrow u \leq F(Q\left( u\right)) \leq F(x).\] Por otro lado como \(Q\) también es monótona: \[u \leq F(x) \Rightarrow Q\left( u\right) \leq Q(F(x)) \leq x\]
A partir de este resultado se deduce el siguiente algoritmo general para simular una distribución de probabilidad discreta.
Algoritmo 5.2 (de transformación cuantil)
Generar \(U\sim \mathcal{U}\left( 0,1\right)\).
Devolver \(X=Q\left( U\right)\).
El principal problema es el cálculo de \(Q\left( U\right)\). En este caso, suponiendo por comodidad que los valores que toma la variable están ordenados (\(x_{1}<x_{2}<\cdots\)), la función cuantil será: \[\begin{array}{ll} Q\left( U\right) &=\inf \left\{ x_{j}:\sum_{i=1}^{j}p_{i}\geq U\right\} \\ &=x_{k}\text{, tal que }\sum_{i=1}^{k-1}p_{i}<U\leq \sum_{i=1}^{k}p_{i} \end{array}\]
Para encontrar este valor se puede emplear el siguiente algoritmo:
Algoritmo 5.3 (de transformación cuantil con búsqueda secuencial)
Generar \(U\sim \mathcal{U}\left( 0,1\right)\).
Hacer \(I=1\) y \(S=p_{1}\).
Mientras \(U>S\) hacer \(I=I+1\) y \(S=S+p_{I}\)
Devolver \(X=x_{I}\).
Este algoritmo no es muy eficiente, especialmente si el número de posibles valores de la variable es grande.
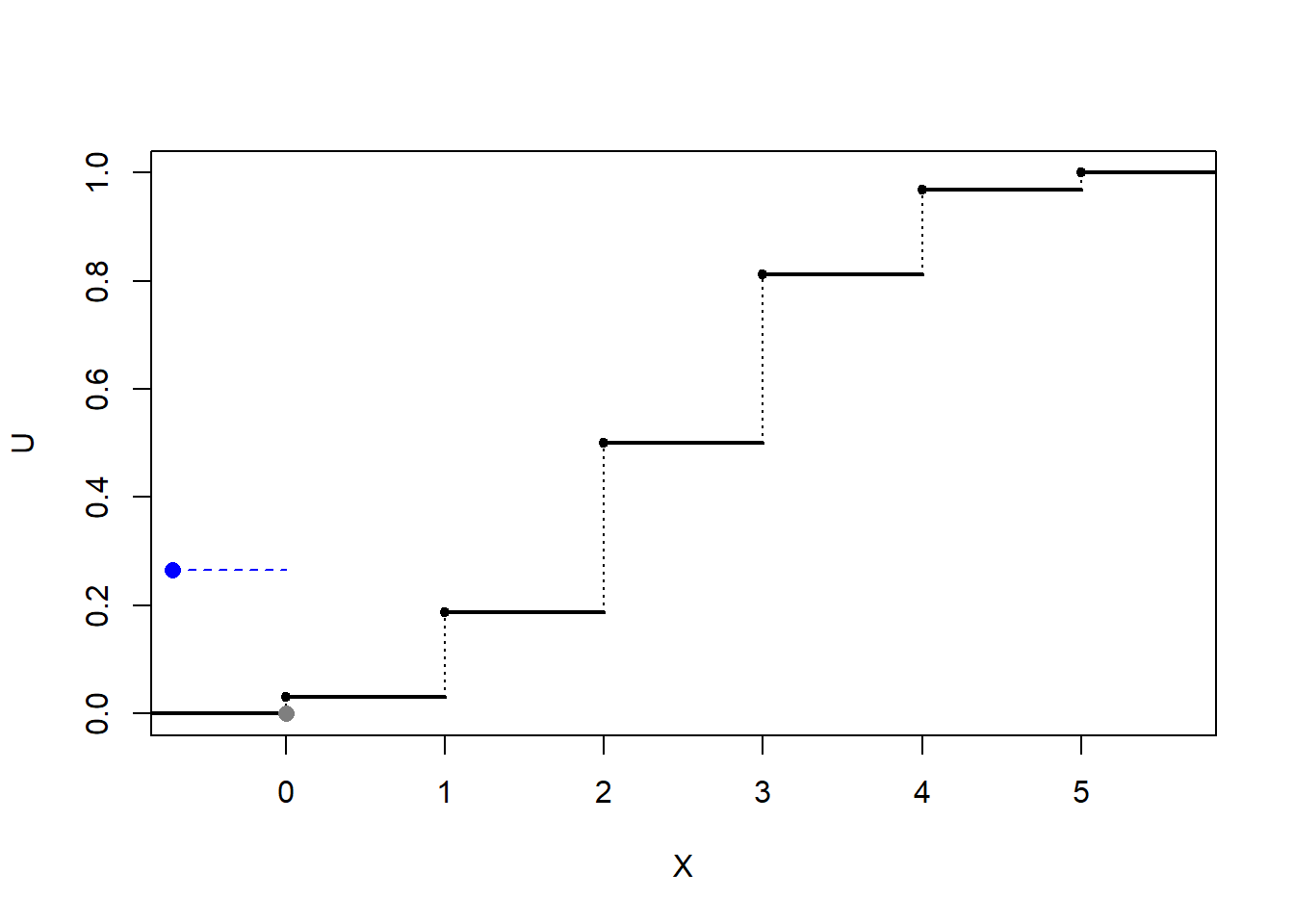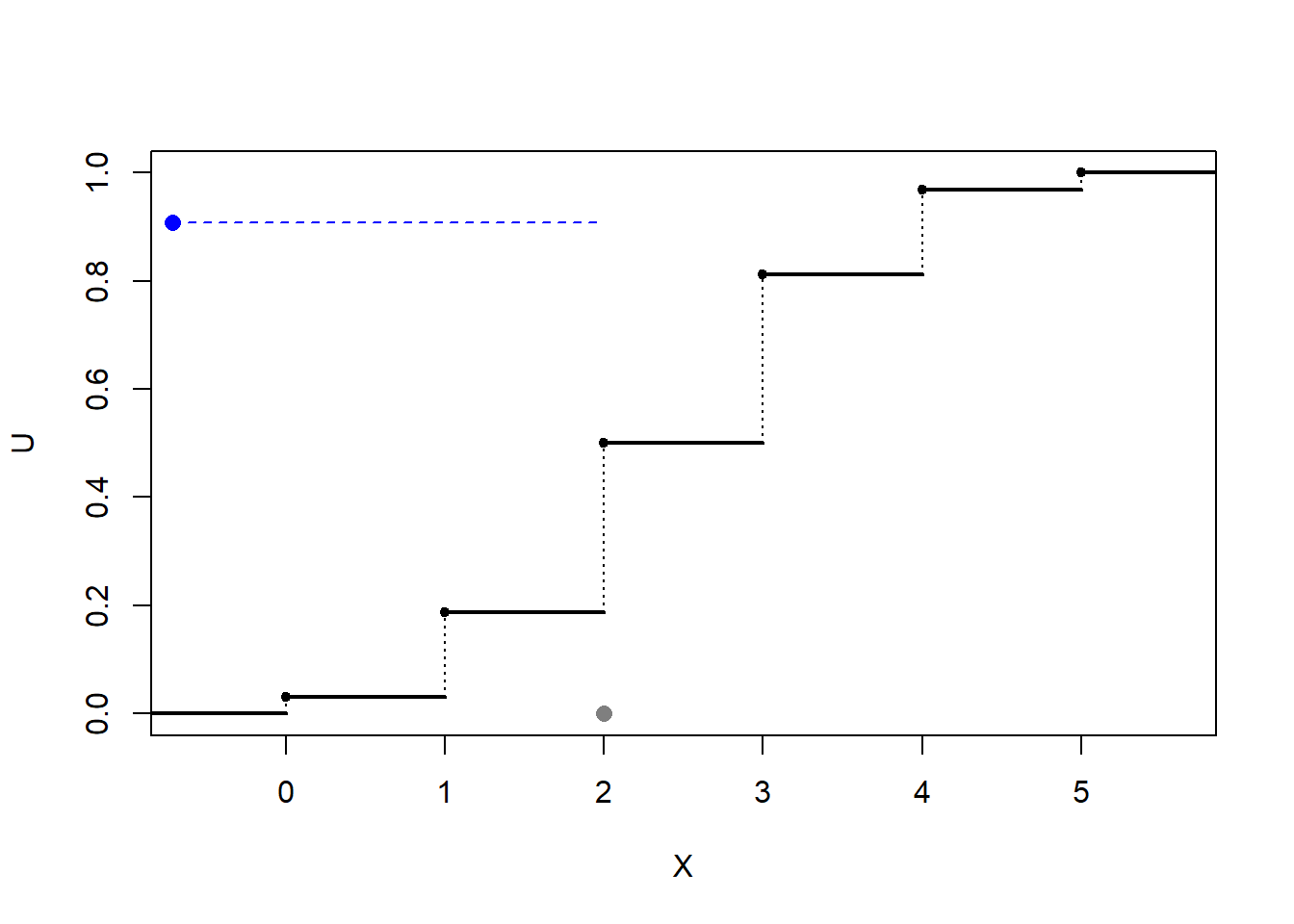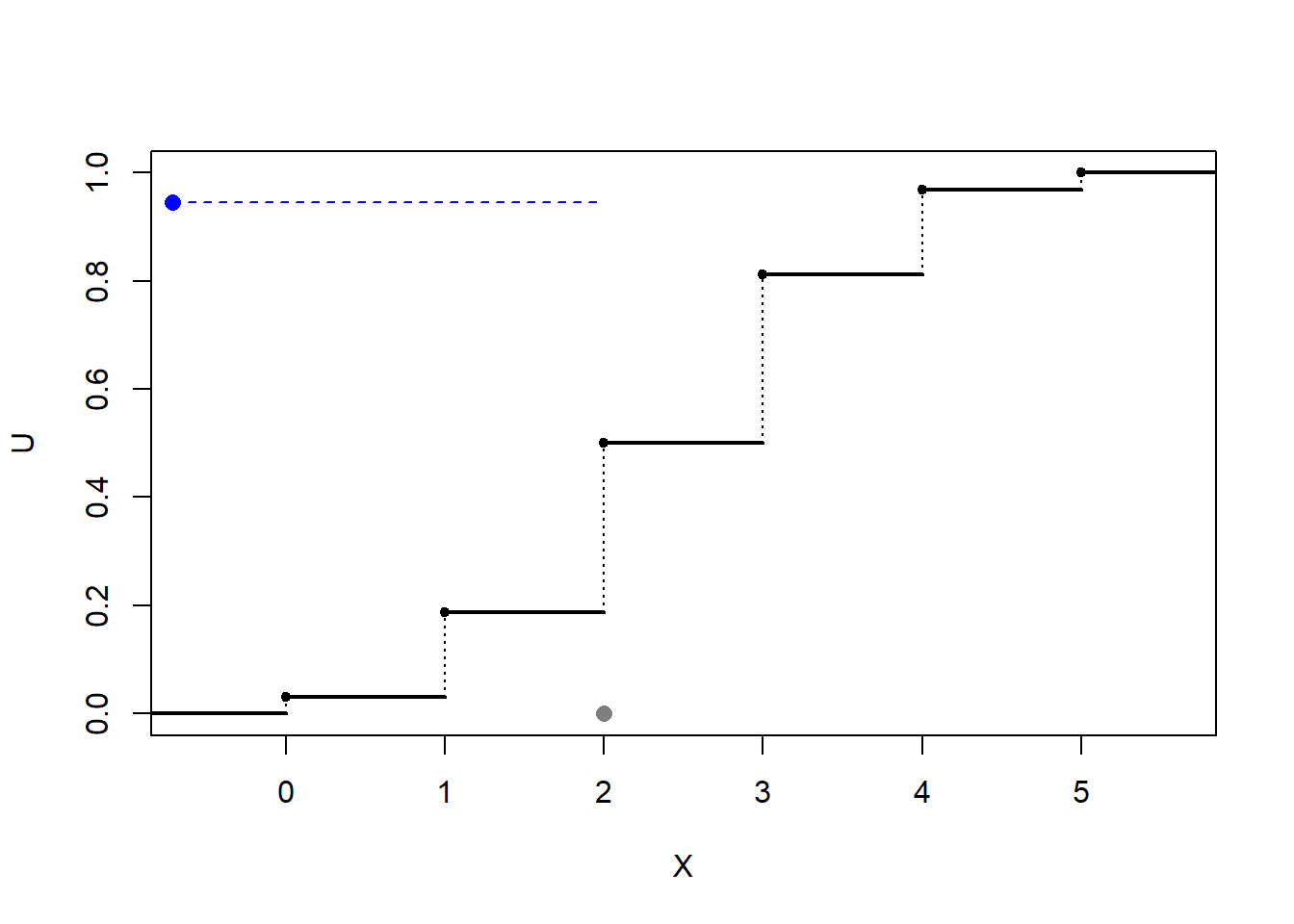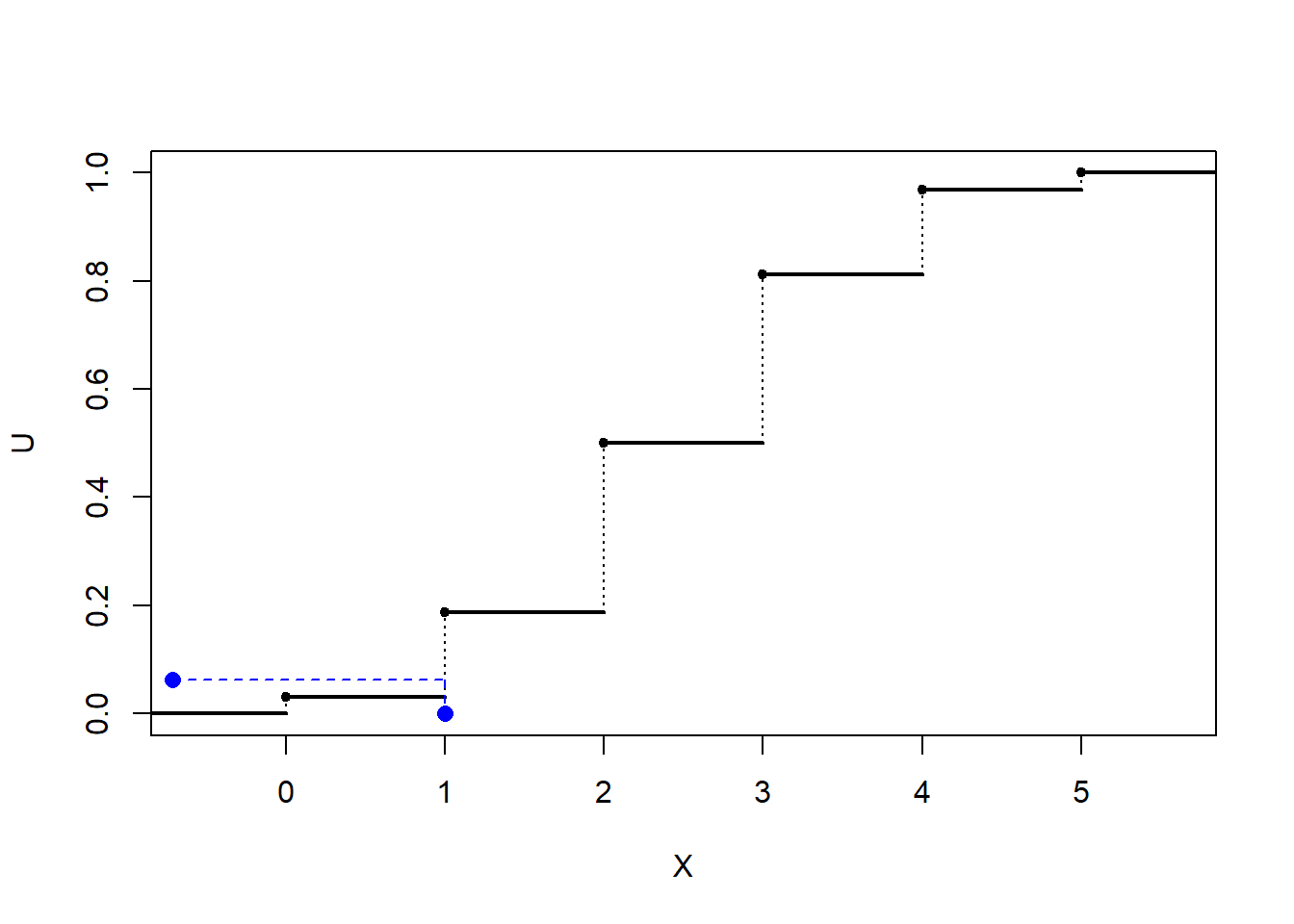
Figura 5.1: Ilustración de la simulación de una distribución discreta mediante transformación cuantil (con búsqueda secuencial).
Nota:. El algoritmo anterior es válido independientemente de que los valores que toma la variable estén ordenados.
Si la variable toma un número finito de valores, se podría implementar en R de la siguiente forma:
rpmf0 <- function(x, prob = 1/length(x), n = 1000) {
X <- numeric(n)
U <- runif(n)
for(j in 1:n) {
i <- 1
Fx <- prob[1]
while (Fx < U[j]) {
i <- i + 1
Fx <- Fx + prob[i]
}
X[j] <- x[i]
}
return(X)
}Adicionalmente, para disminuir ligeramente el tiempo de computación, se pueden almacenar las probabilidades acumuladas en una tabla.
Este algoritmo está implementado en la función rpmf() del paquete simres (fichero rpmf.R), que ademas devuelve el número de comparaciones en un atributo ncomp:
library(simres)
rpmf## function(x, prob = 1/length(x), n = 1000, as.factor = FALSE) {
## # Numero de comparaciones
## ncomp <- 0
## # Inicializar FD
## Fx <- cumsum(prob)
## # Simular
## X <- numeric(n)
## U <- runif(n)
## for(j in 1:n) {
## i <- 1
## while (Fx[i] < U[j]) i <- i + 1
## X[j] <- x[i]
## ncomp <- ncomp + i
## }
## if(as.factor) X <- factor(X, levels = x)
## attr(X, "ncomp") <- ncomp
## return(X)
## }
## <bytecode: 0x00000233cd43ff70>
## <environment: namespace:simres>Ejemplo 5.1 (Simulación de una binomial mediante el método de la transformación cuantil)
Empleamos la rutina anterior para para generar una muestra de \(nsim=10^{5}\) observaciones de una variable \(\mathcal{B}(10,0.5)\) y obtenemos el tiempo de CPU empleado:
Calcular también la media muestral (compararla con la teórica \(np\)) y el número medio de comparaciones para generar cada observación.
Empleamos la rutina anterior para generar las simulaciones:
set.seed(1)
n <- 10
p <- 0.5
nsim <- 10^5
x <- 0:n
pmf <- dbinom(x, n, p)
system.time( rx <- rpmf(x, pmf, nsim) )## user system elapsed
## 0.03 0.00 0.03A partir de ellas podríamos aproximar el valor esperado:
mean(rx)## [1] 4.997aunque en este caso el valor teórico es conocido \(np\) = 5.
Calculamos el número medio de comparaciones para generar cada observación:
ncomp <- attr(rx, "ncomp")
ncomp/nsim## [1] 5.997# Se verá más adelante que el valor teórico es sum((1:length(x))*pmf)Representamos la aproximación por simulación de la función de masa de probabilidad y la comparamos con la teórica:
res <- table(rx)/nsim
# res <- table(factor(rx, levels = x))/nsim
plot(res, ylab = "frecuencia relativa", xlab = "valor")
points(x, pmf, pch = 4, col = "blue") # Comparación teórica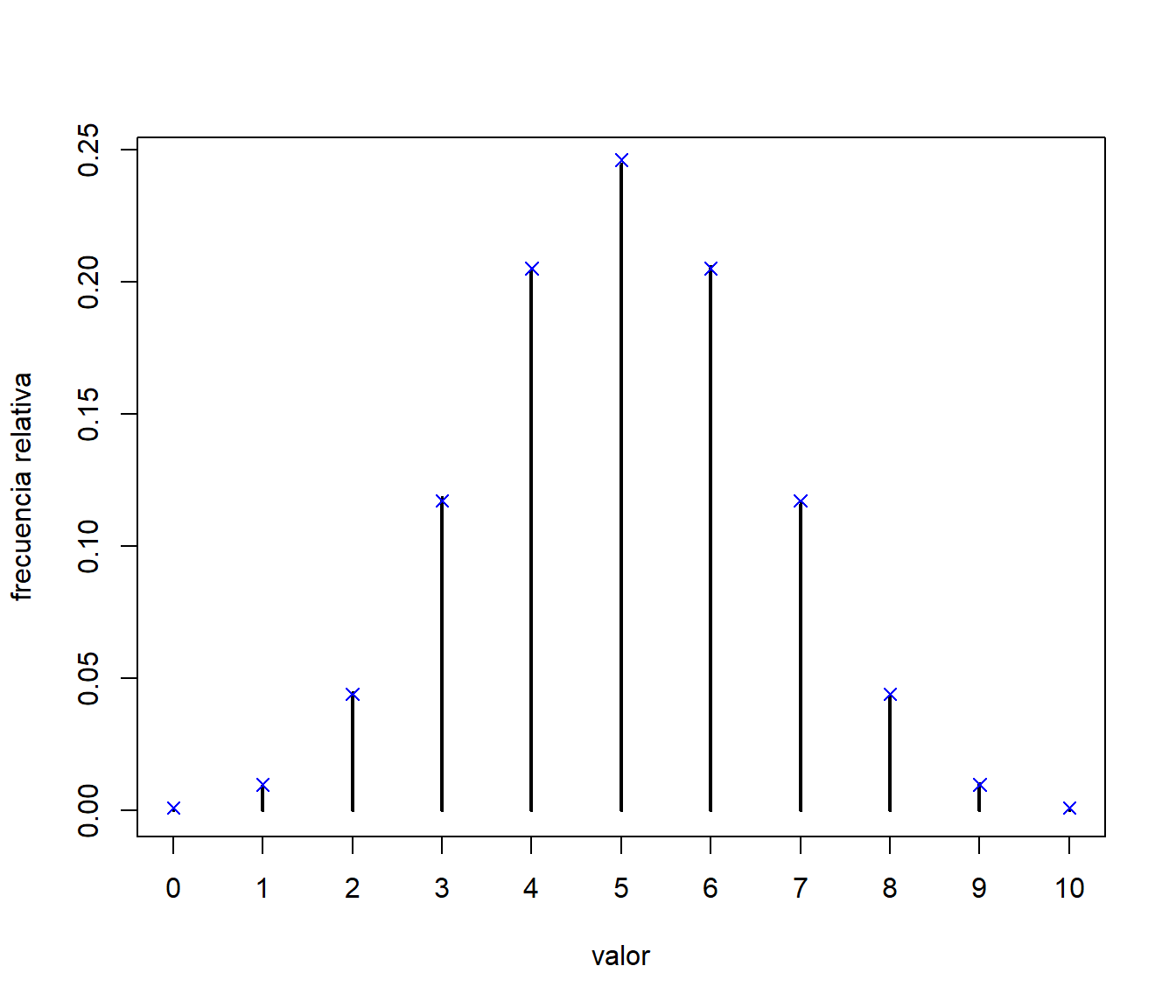
Figura 5.2: Comparación de las frecuencias relativas de los valores generados, mediante el método de la transformación cuantil, con las probabilidades teóricas.
También podríamos realizar comparaciones numéricas:
res <- as.data.frame(res)
names(res) <- c("x", "psim")
res$pteor <- pmf
print(res, digits = 2)## x psim pteor
## 1 0 0.00100 0.00098
## 2 1 0.00981 0.00977
## 3 2 0.04457 0.04395
## 4 3 0.11865 0.11719
## 5 4 0.20377 0.20508
## 6 5 0.24477 0.24609
## 7 6 0.20593 0.20508
## 8 7 0.11631 0.11719
## 9 8 0.04415 0.04395
## 10 9 0.01021 0.00977
## 11 10 0.00083 0.00098# Máximo error absoluto
max(abs(res$psim - res$pteor))## [1] 0.0014625# Máximo error absoluto porcentual
100*max(abs(res$psim - res$pteor) / res$pteor)## [1] 15.008Nota:. Puede ocurrir que no todos los valores sean generados en la simulación.
En el código anterior si length(x) > length(psim), la sentencia res$pteor <- pmf generará un error.
Una posible solución sería trabajar con factores (llamar a la función rpmf() con as.factor = TRUE o emplear res <- table(factor(rx, levels = x))/nsim).
5.1.1 Eficiencia del algoritmo
Si consideramos la variable aleatoria \(\mathcal{I}\) correspondiente a las etiquetas, su función de masa de probabilidad sería: \[\begin{array}{l|ccccc} i & 1 & 2 & \cdots & n & \cdots \\ \hline P\left( \mathcal{I}=i\right) & p_{1} & p_{2} & \cdots & p_{n} & \cdots \end{array}\] y el número de comparaciones en el paso 3 sería un valor aleatorio de esta variable. Una medida de la eficiencia del algoritmo de la transformación cuantil es el número medio de comparaciones23: \[E\left( \mathcal{I}\right) =\sum_i ip_{i}.\]
Para disminuir el número esperado de comparaciones podemos reordenar los valores \(x_{i}\) de forma que las probabilidades correspondientes sean decrecientes. Esto equivale a considerar un etiquetado \(l\) de forma que: \[p_{l\left( 1\right) }\geq p_{l\left( 2\right) }\geq \cdots \geq p_{l\left( n\right) }\geq \cdots\]
Ejemplo 5.2 (Simulación de una binomial, continuación)
Podemos repetir la simulación del Ejemplo 5.1 anterior ordenando previamente las probabilidades en orden decreciente y también empleando la función sample() de R.
set.seed(1)
tini <- proc.time()
# Ordenar
ind <- order(pmf, decreasing = TRUE)
# Generar
rx <- rpmf(x[ind], pmf[ind], nsim)
# Tiempo de CPU
tiempo <- proc.time() - tini
tiempo## user system elapsed
## 0.02 0.00 0.02# Número de comparaciones
ncomp <- attr(rx, "ncomp")
ncomp/nsim## [1] 3.0837sum((1:length(x))*pmf[ind]) # Valor teórico## [1] 3.084Como ya se comentó, en R se recomienda emplear la función sample()
(implementa eficientemente el método de Alias descrito en la Sección 5.3):
system.time( rx <- sample(x, nsim, replace = TRUE, prob = pmf) )## user system elapsed
## 0 0 0Realmente, cuando la variable toma un número finito de valores: \(x_{1}\), \(x_{2}\), \(\ldots\), \(x_{n}\), no sería necesario hacer la última comprobación \(U>\sum_{i=1}^{n}p_{i}=1\) y se generaría directamente \(x_{n}\), por lo que el número medio de comparaciones sería: \[\sum_{i=1}^{n-1}ip_{i}+\left( n-1\right) p_{n}.\]↩︎