8.2 Estratificación
Si se divide la población en estratos y se genera en cada uno un número de observaciones proporcional a su tamaño (a la probabilidad de cada uno) nos aseguramos de que se cubre el dominio de interés y se puede acelerar la convergencia.
- Por ejemplo, para generar una muestra de tamaño \(n\) de una \(\mathcal{U}\left( 0,1\right)\), se pueden generar \(l=\frac{n}{k}\) observaciones (\(1\leq k\leq n\)) de la forma: \[U_{j_{1}},\ldots,U_{j_{l}}\sim \mathcal{U}\left( \frac{(j-1)}{k},\frac{j}{k}\right) \text{ para }j=1,...,k.\]
Si en el número de obsevaciones se tiene en cuenta la variabilidad en el estrato se puede obtener una reducción significativa de la varianza.
Ejemplo 8.2 (muestreo estratificado de una exponencial)
Supóngase el siguiente problema (absolutamente artificial pero ilustrativo para comprender esta técnica). Dada una muestra de tamaño 10 de una población con distribución: \[X \sim \mathcal{Exp}\left( 1 \right),\] se desea aproximar la media poblacional (es sobradamente conocido que es 1) a partir de 10 simulaciones. Supongamos que para evitar que, por puro azar, exista alguna zona en la que la exponencial toma valores, no representada en la muestra simulada de 10 datos, se consideran tres estratos. Por ejemplo, el del 40% de valores menores, el siguiente 50% de valores (intermedios) y el 10% de valores más grandes para esta distribución.
El algoritmo de inversión (simplificado) para simular una \(\mathcal{Exp}\left(1\right)\) es:
Generar \(U\sim \mathcal{U}\left( 0,1\right)\).
Hacer \(X=-\ln U\).
Dado que, en principio, simulando diez valores \(U_{1},U_{2},\ldots,U_{10}\sim \mathcal{U}\left( 0,1\right)\), no hay nada que nos garantice que las proporciones de los estratos son las deseadas (aunque sí lo serán en media). Una forma de garantizar el que obtengamos 4, 5 y 1 valores, repectivamente, en cada uno de los tres estratos, consiste en simular:
4 valores de \(\mathcal{U}[0.6,1)\) para el primer estrato,
5 valores de \(\mathcal{U}[0.1,0.6)\) para el segundo y
uno de \(\mathcal{U}[0,0.1)\) para el tercero.
Otra forma de proceder consistiría en rechazar valores de \(U\) que caigan en uno de esos tres intervalos cuando el cupo de ese estrato esté ya lleno (lo cual no sería computacionalmente eficiente).
El algoritmo con la estratificación propuesta sería como sigue:
Para \(i=1,2,\ldots, 10\):
Generar \(U_{i}\):
2a. Generar \(U\sim \mathcal{U}\left( 0,1\right)\).
2b. Si \(i\leq4\) hacer \(U_{i} = 0.4 \cdot U + 0.6\).
2c. Si \(4<i\leq9\) hacer \(U_{i} = 0.5 \cdot U + 0.1\).
2d. Si \(i=10\) hacer \(U_{i} = 0.1 \cdot U\).
Devolver \(X_{i}=-\ln U_{i}\).
No es difícil probar que:
\(Var\left( X_{i}\right) = 0.0214644\) si \(i=1,2,3,4\),
\(Var\left( X_{i}\right) = 0.229504\) si \(i=5,6,7,8,9\) y
\(Var\left( X_{10}\right) = 1\).
Como consecuencia: \[Var\left( \overline{X}\right) =\frac{1}{10^{2}}\sum_{i=1}^{10} Var\left( X_{i} \right) = 0.022338\] que es bastante menor que 1 (la varianza en el caso de muestreo aleatorio simple no estratificado).
Ejemplo 8.3 (Integración Monte Carlo con estratificación)
Continuando con el Ejemplo 8.1, aproximaremos la integral empleando la técnica de estratificación, considerando \(k\) subintervalos regularmente espaciados en el intervalo \(\left[ 0, 2 \right]\).
mc.integrale <- function(ftn, a, b, n, k) {
# Integración Monte Carlo con estratificación
l <- n%/%k
int <- seq(a, b, len = k + 1)
x <- runif(l*k, rep(int[-(k + 1)], each = l), rep(int[-1], each = l))
# l uniformes en cada uno de los intervalos [(j-1)/k , j/k]
fx <- sapply(x, ftn)*(b-a)
return(list(valor=mean(fx), error=2*sd(fx)/sqrt(n))) # error mal calculado
}
set.seed(54321)
res <- mc.integral(ftn, a, b, 500)
abline(h = teor, lty = 2, col = "blue")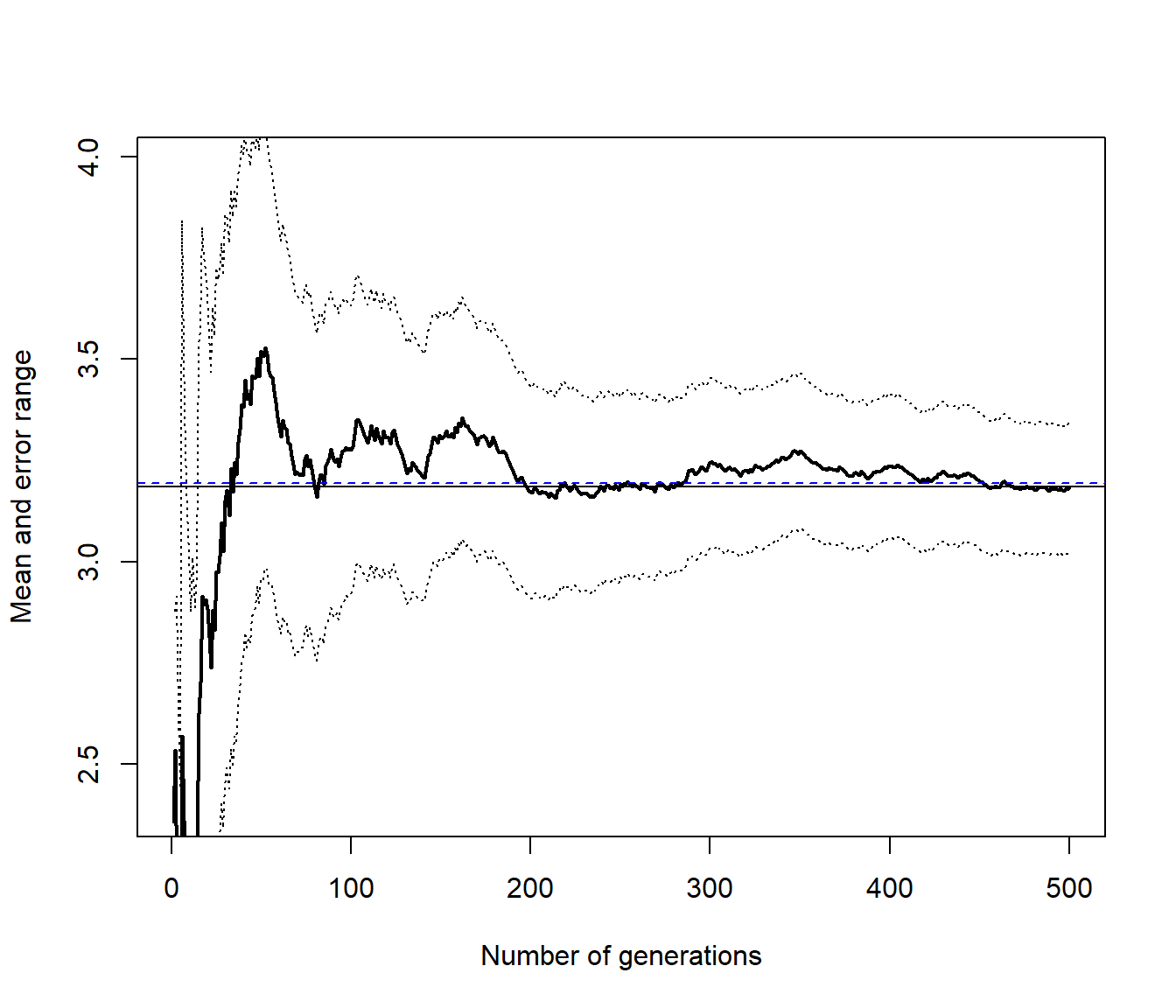
res## $approx
## [1] 3.1846
##
## $max.error
## [1] 0.15973set.seed(54321)
mc.integrale(ftn, a, b, 500, 50)## $valor
## [1] 3.1933
##
## $error
## [1] 0.1598Podríamos estudiar como varía la reducción en la varianza dependiendo del valor de \(k\):
set.seed(54321)
mc.integrale(ftn, a, b, 500, 100)## $valor
## [1] 3.1939
##
## $error
## [1] 0.15991De esta forma no se tiene en cuenta la variabilidad en el estrato. El tamaño de las submuestras debería incrementarse hacia el extremo superior.
Ejercicio 8.1
Repetir el ejemplo anterior considerando intervalos regularmente espaciados en escala exponencial.
# Ejemplo con k = 5
curve(ftn, a, b, ylim = c(0, 4))
abline(h = 0, lty = 2)
abline(v = c(a, b), lty = 2)
k = 5
int <- log(seq(exp(a), exp(b), len = k + 1))
abline(v = int, lty = 3)