B.2 Integración numérica bidimensional

Supongamos que nos interesa aproximar una integral de la forma: \[I=\int_{a_x}^{b_x}\int_{a_y}^{b_y}f(x, y)dy dx\].

Consideraremos como ejemplo: \[\int_{-1}^{1} \int_{-1}^{1} \left( x^2 - y^2 \right) dx dy = 0\].

f2d <- function(x,y) x^2 - y^2

Es habitual (especialmente en simulación) que la función se evalúe en una rejilla:

ax = -1
ay = -1
bx = 1
by = 1
nx = 21
ny = 21
x <- seq(ax, bx, length = nx)
y <- seq(ay, by, length = ny)
z <- outer(x, y, f2d)

hx <- x[2]-x[1]
hy <- y[2]-y[1]

B.2.1 Representación gráfica

Puede ser de utilidad las herramientas de los paquetes plot3D y plot3Drgl (también se pueden utilizar las funciones spersp, simage, spoints y splot del paquete npsp).

if(!require(plot3D)) stop('Required pakage `plot3D` not installed.')

# persp3D(z = z, x = x, y = y)

persp3D.f2d <- function(f2d, ax=-1, bx=1, ay=-1, by=1, nx=21, ny=21, ...) { 
  x <- seq(ax, bx, length = nx)
  y <- seq(ay, by, length = ny)
  z <- outer(x, y, f2d)
  persp3D(x, y, z, ...)
}

persp3D.f2d(f2d, -1, 1, -1, 1, 50, 50, ticktype = "detailed")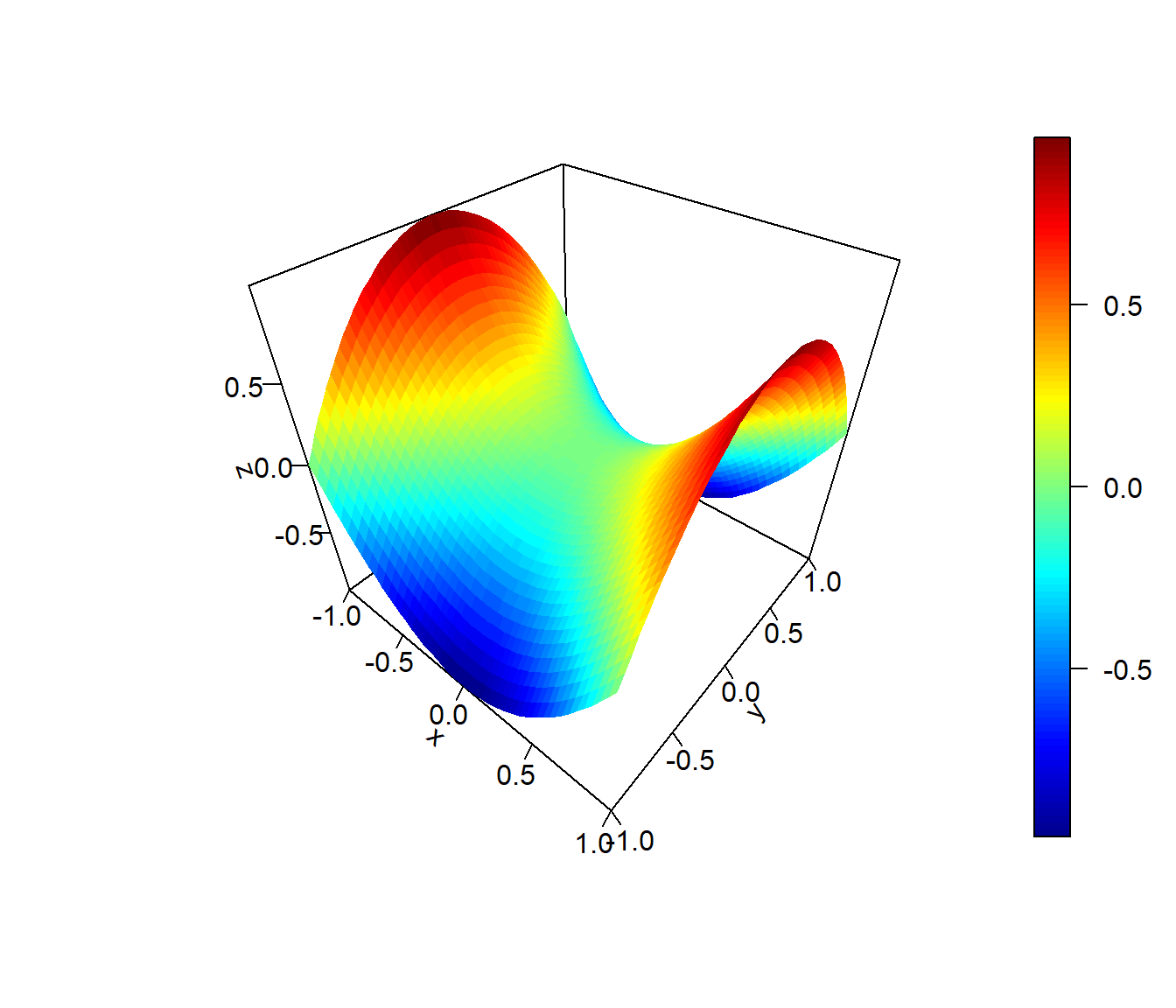 

B.2.2 Método del trapezoide

Error \(O(n^{-\frac{2}{d}})\).

trapezoid.mat <- function(z, hx, hy) { 
# Integración numérica bidimensional
# utilizando el método del trapezoide (se aproxima f linealmente)
  f.vec <- apply(z, 1, function(x) trapezoid.vec(x, hx))
  return(trapezoid.vec(f.vec, hy)) 
}

# trapezoid.mat(z, hx, hy) 

trapezoid.f2d <- function(f2d, ax=-1, bx=1, ay=-1, by=1, nx=21, ny=21) { 
  x <- seq(ax, bx, length = nx)
  y <- seq(ay, by, length = ny)
  hx <- x[2]-x[1]
  hy <- y[2]-y[1]
  z <- outer(x, y, f2d)
  trapezoid.mat(z, hx, hy)
}

trapezoid.f2d(f2d, -1, 1, -1, 1, 101, 101) 

## [1] -8.8818e-18

B.2.3 Comandos de R

Suponiendo que la función es vectorial, podemos emplear:

integrate( function(y) {
    sapply(y, function(y) {
      integrate(function(x) f2d(x,y), ax, bx)$value }) }, 
    ay, by)

## -2.7756e-17 with absolute error < 1.1e-14

Si la función no es vectorial y solo admite parámetros escalares:

integrate(function(y) {
    sapply(y, function(y) {
      integrate(function(x) {
        sapply(x, function(x) f2d(x,y)) }, ax, bx)$value }) },
    ay, by)

Fuente: tolstoy.newcastle.edu.au.

Alternativamente se podría emplear la función cubintegrate() del paquete cubature.